Với giải SGK Toán 11 Chân trời sáng tạo trang 60 chi tiết trong Bài 3: Cấp số nhân giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Giải Toán 11 trang 60 Tập 1 (Chân trời sáng tạo)
a) u1 = 105; q = 0,1; n = 5;
b) u1 = 10; u2 = – 20; n = 5.
Lời giải:
a) (un) là cấp số nhân có số hạng đầu u1 = 105 và công bội q = 0,1 nên có số hạng tổng quát là: un = u1.qn-1 = 105.(0,1)n – 1 .
Khi đó ta có: u5 = 105.(0,1)5 – 1 = 105.(0,1)4 = 10.
Tổng 5 số hạng đầu tiên của cấp số nhân (un) là:
.
b) (un) là cấp số nhân có số hạng đầu u1 = 10 và công bội q = nên có số hạng tổng quát là: un = u1.qn-1 = 10.(– 2)n – 1 .
Khi đó ta có: u5 = 10.(– 2)5 – 1 = 10.(– 2)4 = 160.
Tổng 5 số hạng đầu tiên của cấp số nhân (un) là:
.
Lời giải:
Dãy số đã cho là một cấp số nhân với số hạng đầu u1 = 120 và công sai .
Khi đó công thức số hạng tổng quát của cấp số nhân này là: un = 120..
Độ cao của quả bóng sau lần rơi thứ 10 là u10 = 120.= .
Tổng độ cao của quả bóng sau 10 lần rơi đầu tiên là:
.
Bài tập
Bài 1 trang 60 Toán 11 Tập 1: Trong các dãy số sau, dãy số nào là cấp số nhân?
a) un = 3.(– 2)n;
b) un = (– 1)n.7n;
c) 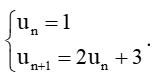
Lời giải:
a) Ta có:
u1 = 3.(0 – 2)1 = 3.(– 2) = – 6.
un+1 = 3.(– 2)n+1 = 3.(– 2)n.(– 2) = un.( – 2).
Vậy dãy số un = 3.(– 2)n là một cấp số nhân có số hạng đầu là u1 = – 6 và công sai d = – 2.
b) Ta có:
u1 = (– 1)1.71 = – 7;
un + 1 = (– 1)n+1.7n+1 = (– 1)n.(– 1).7n.7 = un.(– 7).
Vậy dãy số đã cho là một cấp số nhân có số hạng đầu là u1 = – 7 và công sai d = – 7.
c) Ta có: <; un+1 = 5; un+2 = 13, ...
Dãy số này không phải cấp số nhân vì .
Bài 2 trang 60 Toán 11 Tập 1: Tìm số hạng đầu và công bội của cấp số nhân (un), biết:
a) 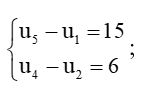 ;
;
b) 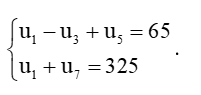 .
.
Lời giải:
a) 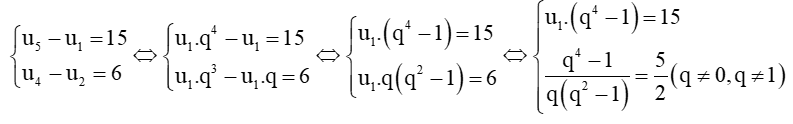
Xét 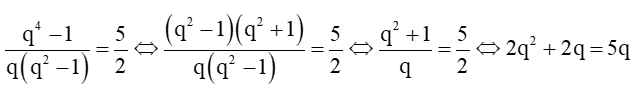
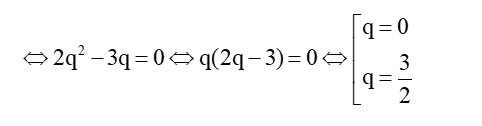
Vì u5 ≠ 0 nên loại q = 0 do đó q = thỏa mãn.
u1 = 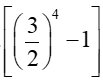 = 15 u1 = .
= 15 u1 = .
Vậy dãy số có số hạng đầu là và công sai q = .
b) 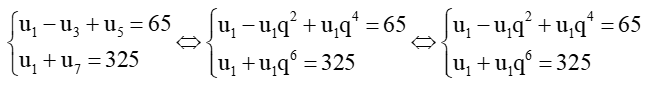
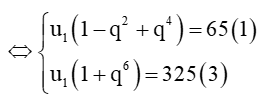
Lấy vế với vế của (1) chia cho (3) ta được
.
⇔ q6 – 5q4 + 5q2 – 4 = 0
⇔ q6 – 4q4 – q4 + 4q2 + q2 – 4 = 0
⇔ q4(q2 – 4) – q2(q2 – 4) + q2 – 4 = 0
⇔ (q2 – 4)(q4 – q2 + 1) = 0
⇔ 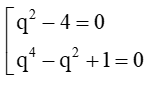
⇔ q = 2 hoặc q4 – q2 + 1 = 0 (vô lí)
Với q = 2 thì u1 = 5.
Với q = – 2 thì u1 = 5.
Vậy cấp số nhân (un) có số hạng đầu là u1 = 5 và công bội là q = 2 hoặc số hạng đầu là u1 = 5 và công bội là q = – 2.
b) Viết sáu số xen giữa các số – 2 và 256 để được cấp số nhân có tám số hạng. Nếu viết tiếp số hạng thứ 15 là bao nhiêu?
Lời giải:
a) Gọi số đo bốn góc của một tứ giác được lập thành một cấp số nhân có công bội q theo thứ tự từ bé đến lớn là: α; β; γ; φ.
Ta có: β = αq, γ = α.q2, φ = α.q3.
Ta lại có: φ = 8α nên q3 = 8 ⇔ q = 2.
Do đó cấp số cộng trên trở thành: α; 2α; 4α; 8α.
Tổng bốn góc trong tứ giác bằng 360° nên α + 2α + 4α + 8α = 360°
⇔ 15α = 360°
⇔ α = 24°
Vậy số đo của các góc trong tứ giác lần lượt là 24°; 48°; 72°; 96°.
b) Cấp số nhân đã cho có u1 = – 2 và u8 = 256.
Ta có: u8 = u1q7 = (– 2).q7 = 256
⇔ q = – 2
Suy ra các số hạng xen giữa hai số – 2 và 256 là: 4; – 8; 16; – 32; 64; – 128.
Số hạng thứ 15 của dãy là: u15 = (– 2).( – 2)14 = (– 2)15 = 0 – 32 768.
Lời giải:
Ta có: là một cấp số cộng nên ta có:
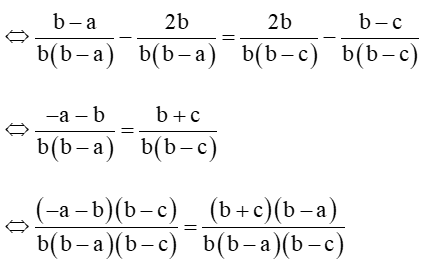
(-a-b)(b-c) = (b+c)(b-a)
⇔ – ab + ac – b2 + bc = b2 – ab + bc – ac
⇔ 2b2 – 2ac = 0
⇔ b2 = ac.
Bài 5 trang 60 Toán 11 Tập 1: Tính các tổng sau:
a) ;
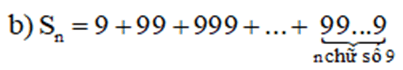
Lời giải:
Dãy số lập thành một cấp số nhân có số hạng đầu u1 = 1 và công bội q = .
Khi đó tổng của n số hạng đầu của cấp số nhân là:
.
Lời giải:
Số lượng vi khuẩn sau mỗi phút lập thành một cấp số nhân (un), với số hạng đầu u1 = 1, công bội q = 2.
Suy ra số hạng tổng quát un = 2n-1.
Vậy sau 20 phút số lượng vi khuẩn trong ống nghiệm là: u20 = 219 (vi khuẩn).
Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác:
a) u1 = 105; q = 0,1; n = 5;
Bài 1 trang 60 Toán 11 Tập 1: Trong các dãy số sau, dãy số nào là cấp số nhân a) un = 3.(– 2)n;
Bài 2 trang 60 Toán 11 Tập 1: Tìm số hạng đầu và công bội của cấp số nhân (un), biết: a) 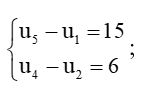 ;
;
Bài 5 trang 60 Toán 11 Tập 1: Tính các tổng sau: a) ;
Xem thêm lời giải sách giáo khoa Toán 11 Chân trời sáng tạo hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.