Toptailieu.vn biên soạn và giới thiệu lời giải Vật lí 11 (Kết nối tri thức) Bài 3: Vận tốc, gia tốc trong dao động điều hoà hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi từ đó học tốt môn Vật lí 11.

Vật lí 11 (Kết nối tri thức) Bài 3: Vận tốc, gia tốc trong dao động điều hoà

Khởi động trang 14 Vật Lí 11: Ta có thể dựa vào đồ thị (x – t) của dao động điều hoà để xác định vận tốc và gia tốc của vật được không?

Lời giải:

Ta hoàn toàn có thể dựa vào đồ thị (x – t) của dao động điều hoà để xác định vận tốc và gia tốc của vật được. Vì từ đồ thị (x – t) ta có thể lập được phương trình dao động điều hoà của vật, từ đó lập được phương trình của vận tốc v và gia tốc a:

$v=x\text{'}=-\omega A\sin \left(\omega t+\phi \right)$

$a=v\text{'}=-{\omega }^{2}A\cos \left(\omega t+\phi \right)$

Hoạt động trang 14 Vật lí 11: Đặt một thước kẻ (loại 20 cm) cho mép của thước tiếp xúc với đồ thị li độ - thời gian (Hình 3.1) ở một số điểm C, D, E, G, H. Từ độ dốc của thước hãy so sánh độ lớn vận tốc của vật tại các điểm C, E, H

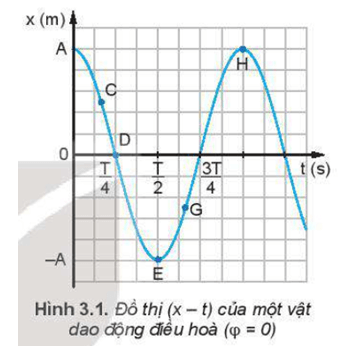
Lời giải:

Sử dụng thước để xác định độ dốc của đồ thị tại các điểm C, E, H ta thấy được:

- Độ dốc tại điểm E và H bằng nhau và bằng 0.

- Độ dốc tại điểm C khác 0.

⇒ Độ lớn vận tốc của vật tại điểm C lớn hơn điểm E và H.

Câu hỏi trang 15 Vật lí 11: So sánh đồ thị của vận tốc (Hình 3.2) với đồ thị của li độ (Hình 3.1), hãy cho biết vận tốc sớm pha hay trễ pha bao nhiêu so với li độ.

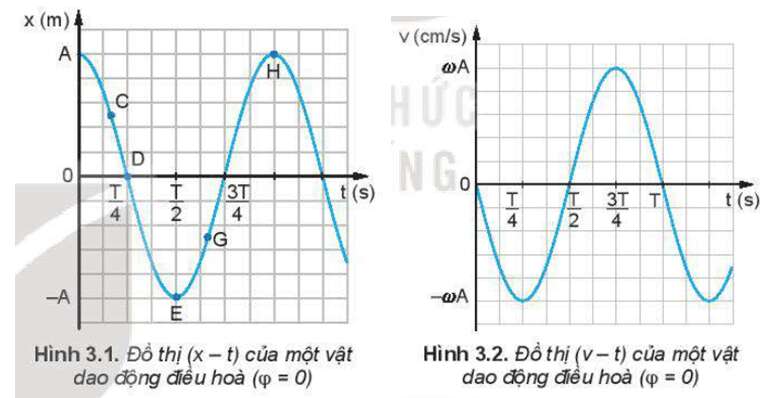
Lời giải:

- Từ đồ (x – t) ta thấy tại thời điểm ban đầu (t = 0) vật đang ở vị trí biên dương và tiến về VTCB (đi theo chiều âm) nên phương trình dao động có dạng: $x=A\cos \left(\omega t\right)$

- Từ đồ thị (v – t) ta thấy tại thời điểm ban đầu (t = 0) vận tốc đang có giá trị bằng 0 và đang giảm dần nên phương trình vận tốc có dạng: $v=v_{\max }\cos \left(\omega t+\frac{\pi }{2}\right)$

Chứng tỏ vận tốc đang dao động sớm pha hơn li độ góc $\frac{\pi }{2}$

Câu hỏi trang 15 Vật lí 11: Trong các khoảng thời gian từ 0 đến $\frac{T}{4}$ , từ $\frac{T}{4}$ đến $\frac{T}{2}$ , từ $\frac{T}{2}$ đến $\frac{\mathrm{3T}}{4}$ , từ $\frac{\mathrm{3T}}{4}$ đến T, vận tốc của dao động điều hoà thay đổi như thế nào?

Lời giải:

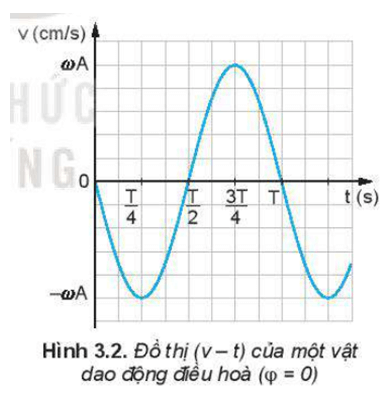
Từ đồ thị 3.2 ta thấy:

- Trong khoảng thời gian từ 0 đến $\frac{T}{4}$, vận tốc có giá trị bằng 0 sau đó giảm dần đến giá trị cực tiểu$-\omega A$.

- Trong khoảng thời gian từ $\frac{T}{4}$ đến $\frac{T}{2}$, vận tốc có giá trị cực tiểu  sau đó tăng dần đến giá trị bằng 0

- Trong khoảng thời gian từ $\frac{T}{2}$ đến $\frac{\mathrm{3T}}{4}$, vận tốc có giá trị bằng 0 sau đó tăng dần đến giá trị cực đại $\omega A$.

- Trong khoảng thời gian từ $\frac{\mathrm{3T}}{4}$ đến T, vận tốc có giá trị cực đại  sau đó giảm dần đến giá trị bằng 0.

Hoạt động trang 15 Vật lí 11: Dùng thước kẻ (loại 20 cm) để xác định xem trên đồ thị (v – t) Hình 3.2, tại thời điểm nào độ dốc của đồ thị bằng 0 và tại thời điểm nào độ dốc của đồ thị cực đại. Từ đó, so sánh độ lớn của gia tốc trên đồ thị (a - t) Hình 3.3 ở các thời điểm tương ứng.

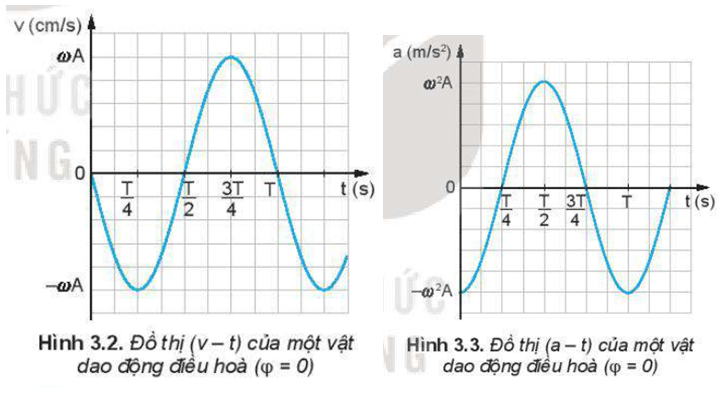
Lời giải:

- Từ đồ thị 3.2 và dùng thước kẻ để xác định độ dốc thì ta thấy tại thời điểm $\frac{T}{2}$ và T thì độ dốc của đồ thị (v – t) có độ lớn là lớn nhất; tại thời điểm $\frac{T}{4}$ và $\frac{\mathrm{3T}}{4}$ độ dốc của đồ thị (v – t) có độ lớn bằng 0.

- So sánh độ lớn gia tốc trên đồ thị (a – t):

+ Tại thời điểm ban đầu (t = 0): vận tốc có độ lớn bằng 0, gia tốc có độ lớn cực đại ${\omega }^{2}A$

+ Tại thời điểm $\frac{T}{4}$: vận tốc có độ lớn cực đại , gia tốc bằng 0.

+ Tại thời điểm $\frac{T}{2}$: vận tốc bằng 0, gia tốc có độ lớn cực đại ${\omega }^{2}A$

- Tại thời điểm $\frac{\mathrm{3T}}{4}$: vận tốc có độ lớn cực đại , gia tốc bằng 0.

- Tại thời điểm T: vận tốc bằng 0, gia tốc có độ lớn cực đại ${\omega }^{2}A$

Hoạt động trang 15 Vật lí 11: Phương trình dao động của một vật là $x=5\cos 4\pi t\left(cm\right)$ . Hãy viết phương trình vận tốc, gia tốc và vẽ đồ thị li độ, vận tốc, gia tốc theo thời gian của vật.

Lời giải:

Phương trình vận tốc:

$v=x\text{'}=-4\pi .5\sin 4\pi t=20\pi \cos \left(4\pi t+\frac{\pi }{2}\right)\left(cm/s\right)$

Phương trình gia tốc:

$a=-{\omega }^{2}x=-{\left(4\pi \right)}^2.5\cos 4\pi t=80{\pi }^2\cos \left(4\pi t+\pi \right)\left(cm/s^2\right)$

Vẽ đồ thị li độ, vận tốc, gia tốc theo thời gian của vật

Câu hỏi trang 15 Vật lí 11: So sánh đồ thị Hình 3.3 và Hình 3.1 ta có nhận xét gì về pha của li độ và gia tốc của một dao động.

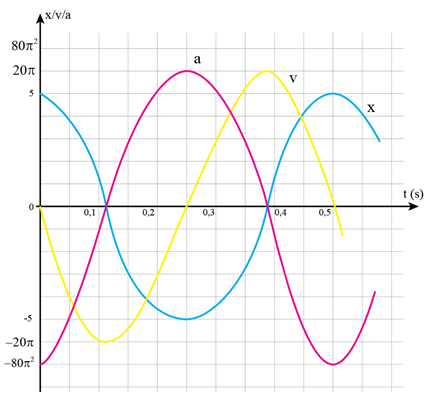
Lời giải:

Từ đồ thị ta có thể thấy li độ và gia tốc ngược pha với nhau. Cụ thể thì gia tốc sớm pha hơn li độ một góc là π(rad).

Câu hỏi trang 15 Vật lí 11: Trong các khoảng thời gian từ 0 đến $\frac{T}{4}$ , từ $\frac{T}{4}$ đến $\frac{T}{2}$ , từ $\frac{T}{2}$ đến $\frac{\mathrm{3T}}{4}$ , từ $\frac{\mathrm{3T}}{4}$ đến T, gia tốc của dao động thay đổi như thế nào?

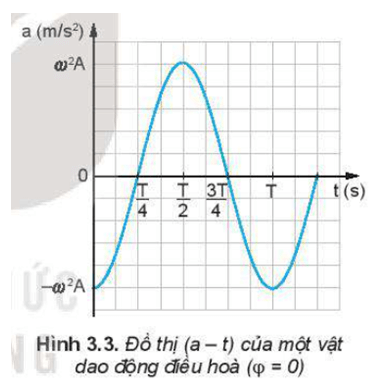
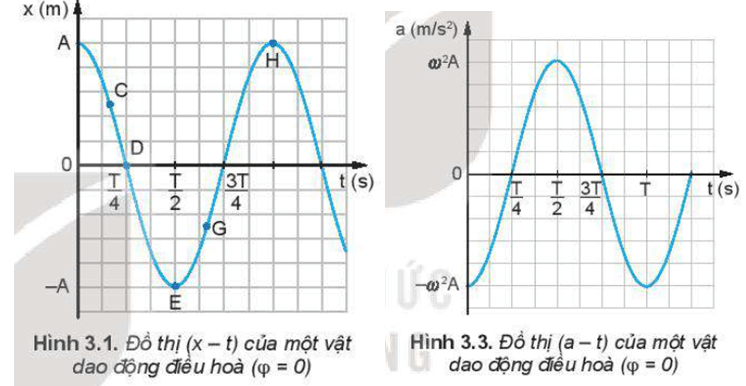
Lời giải:

- Tại thời điểm ban đầu (t = 0): gia tốc có giá trị $-{\omega }^{2}A$ và tăng dần.

- Tại thời điểm $\frac{T}{4}$: gia tốc bằng 0.

- Tại thời điểm $\frac{T}{2}$: gia tốc có giá trị ${\omega }^{2}A$

- Tại thời điểm $\frac{\mathrm{3T}}{4}$: gia tốc bằng 0.

- Tại thời điểm T: gia tốc có giá trị $-{\omega }^{2}A$.

Nếu xét về độ lớn thì gia tốc có độ lớn cực đại ${\omega }^{2}A$ tại các thời điểm 0; $\frac{T}{2}$; T.

Câu hỏi trang 16 Vật lí 11: Một vật dao động điều hoà trên trục Ox. Khi vật qua vị trí cân bằng thì tốc độ của nó là 20 cm/s. Khi vật có tốc độ là 10 cm/s thì gia tốc của nó có độ lớn là $40\sqrt{3}$ cm/s2. Tính biên độ dao động của vật.

Lời giải:

Tại VTCB, tốc độ của vật $v_{\max }=\omega A=20cm/s$

Khi vật có tốc độ là 10 cm/s thì gia tốc của nó có độ lớn là $40\sqrt{3}$ cm/s²

$\left\{\begin{array}{l}v=-\omega A\sin \left(\omega t+\phi \right)\\ a=-{\omega }^{2}A\cos \left(\omega t+\phi \right)\end{array}\right.\Rightarrow \left\{\begin{array}{l}\sin \left(\omega t+\phi \right)=\frac{-v}{\omega A}\\ \cos \left(\omega t+\phi \right)=\frac{-a}{{\omega }^{2}A}\end{array}\right.$

$\Rightarrow {\sin }^2\left(\omega t+\phi \right)+{\cos }^2\left(\omega t+\phi \right)={\left(\frac{-v}{\omega A}\right)}^2+{\left(\frac{-a}{{\omega }^{2}A}\right)}^2=1$

null

Thay số: $\frac{{10}^2}{{20}^2}+\frac{{\left(40\sqrt{3}\right)}^2{A}^2}{{20}^4}=1\Rightarrow A=5cm$

Câu hỏi trang 16 Vật lí 11: Hình 3.4 là đồ thị li độ – thời gian của một vật dao động điều hoà. Sử dụng đồ thị để tính các đại lượng sau:

a) Tốc độ của vật ở thời điểm t = 0 s.

b) Tốc độ cực đại của vật.

c) Gia tốc của vật tại thời điểm t = 1,0 s.

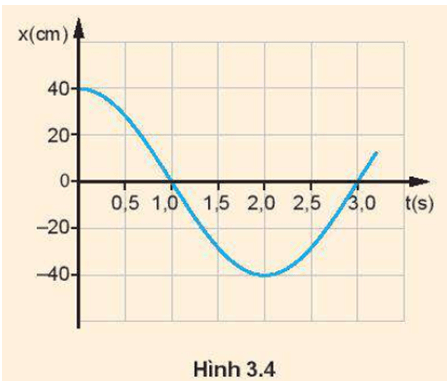
Lời giải:

Từ đồ thị ta xác định được các đại lượng:

- Biên độ: A = 40 cm

- Chu kì: T = 4 s

- Tần số góc: $\omega =\frac{2\pi }{T}=\frac{2\pi }{4}=0,5\pi \left(rad/s\right)$

a) Tại thời điểm t = 0 s:

Vật đang ở biên dương nên vận tốc của vật bằng 0

b) Tốc độ cực đại của vật: $v_{\max }=\omega A=0,5\pi .40=20\pi \left(cm/s\right)$

c) Tại thời điểm t = 1,0 s:

Từ đồ thị, ta thấy tại t = 1s vật đang ở vị trí cân bằng gia tốc của vật bằng 0.

Em có thể trang 16 Vật lí 11: Sử dụng được đồ thị mô tả dao động điều hoà thu được trên dao động kí có thể suy ra các đại lượng vận tốc, gia tốc của vật trong dao động điều hoà.

Lời giải:

Học sinh có thể tham khảo một số đồ thị thu được trên dao động kí để thực hiện theo yêu cầu đề bài.

VD: Một vật dao động điều hòa có đồ thị dao động như hình vẽ:

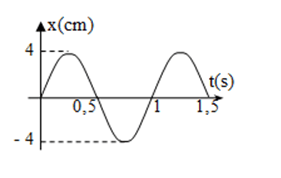
Ta viết được phương trình x = $4cos\left(2\pi t-\frac{\pi }{2}\right)$

Ta có thể suy ra được các đại lượng vận tốc, gia tốc của vật:

+ Tại VTCB: a = 0, v = $\pm 8\pi$(m/s).

+ Tại vị trí biên: a = $\pm 16\pi$(m/s²), v = 0.

Xem thêm các bài giải Vật lí 11 Kết nối tri thức hay, chi tiết khác:

Vật lí 11 (Kết nối tri thức) Bài 4: Bài tập về dao động điều hoà

Vật lí 11 (Kết nối tri thức) Bài 5: Động năng. Thế năng. Sự chuyển hoá năng lượng trong dao động điều hoà

Vật lí 11 (Kết nối tri thức) Bài 6: Dao động tắt dần. Dao động cưỡng bức. Hiện tượng cộng hưởng

Vật lí 11 (Kết nối tri thức) Bài 7: Bài tập về sự chuyển hoá năng lượng trong dao động điều hoà

Vật lí 11 (Kết nối tri thức) Bài 8: Mô tả sóng