Cho tam giác nhọn ABC. Vẽ về phía ngoài tam giác ABC các tam giác đều ABD, ACE

Ngọc Nguyễn Ngày: 01-07-2023 Lớp 11

339

Với giải Bài 13 trang 25 Chuyên đề Toán 11 Cánh Diều chi tiết trong Bài 1: Phép dời hình giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Chuyên đề Toán 11. Mời các bạn đón xem:

Cho tam giác nhọn ABC. Vẽ về phía ngoài tam giác ABC các tam giác đều ABD, ACE

Bài 13 trang 25 Chuyên đề Toán 11: Cho tam giác nhọn ABC. Vẽ về phía ngoài tam giác ABC các tam giác đều ABD, ACE.

a) Xác định ảnh của các điểm D và C quay phép quay tâm A với góc quay φ = 60°.

b) Chứng minh rằng DC = BE.

c) Chứng minh rằng số đo góc giữa hai đường thẳng DC và BE bằng 60°.

Lời giải:

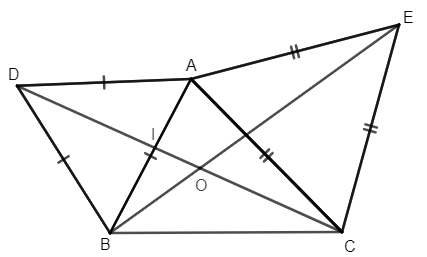
Chuyên đề Toán 11 (Cánh diều) Bài 1: Phép dời hình (ảnh 55)

a) + Vì tam giác ABD đều nên AD = AB và $\hat{D A B} = 60 °$ .

Phép quay với góc quay φ = 60° có chiều quay ngược chiều kim đồng hồ. Do đó, ảnh của điểm D phép quay tâm A với góc quay φ = 60° là điểm B.

+ Vì tam giác ACE đều nên AC = AE và $\hat{C A E} = 60 °$ .

Do đó, ảnh của điểm C phép quay tâm A với góc quay φ = 60° là điểm E.

b) Theo câu a) ta có B và E lần lượt là ảnh của D và C qua phép quay tâm A với góc quay φ = 60°, suy ra DC = BE (phép quay bảo toàn khoảng cách giữa hai điểm bất kì).

c) Gọi O là giao điểm của DC và BE, I là giao điểm của AB và DC.

Ta có phép quay tâm A với góc quay φ = 60° biến góc ADC thành góc ABE nên $\hat{A D C} = \hat{A B E}$ hay $\hat{A D I} = \hat{I B O}$ .

Mà $\hat{A I D} = \hat{B I O}$ (2 góc đối đỉnh), $\hat{A D I} + \hat{A I D} + \hat{D A I} = 180 °$ (tổng ba góc trong tam giác ADI) và $\hat{I B O} + \hat{B I O} + \hat{I O B} = 180 °$ (tổng ba góc trong tam giác IBO).