Chuyên đề Toán 11 (Cánh diều) Bài 2: Phép đồng dạng

Ngọc Nguyễn Ngày: 29-06-2023 Lớp 11

316

Toptailieu.vn biên soạn và giới thiệu lời giải Chuyên đề Toán 11 (Cánh diều) Bài 2: Phép đồng dạng hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi Chuyên đề Toán 11 Bài 2 từ đó học tốt môn Toán 11.

Chuyên đề Toán 11 (Cánh diều) Bài 2: Phép đồng dạng

Khởi động trang 26 Chuyên đề Toán lớp 11: Tranh Đông Hồ là một dòng tranh dân gian Việt Nam, xuất xứ từ làng Đông Hồ (xã Song Hồ, huyện Thuận Thành, tỉnh Bắc Ninh). Tranh được in trên giấy điệp, màu sắc được sử dụng là màu tự nhiên: màu đen từ than lá tre, màu xanh từ lá chàm, màu đỏ từ sỏi,... Nghề làm tranh dân gian Đông Hồ là di sản văn hóa phi vật thể cấp Quốc gia.

(Nguồn: https:vi.wikipedia.org/wki)

Chuyên đề Toán 11 (Cánh diều) Bài 2: Phép đồng dạng (ảnh 1)

Ba bức tranh trong Hình 46 có hình dạng giống hệt nhau nhưng có kích thước to nhỏ khác nhau gợi nên những hình có mối liên hệ gì?

Lời giải:

Ba bức tranh trong Hình 46 có hình dạng giống hệt nhau nhưng có kích thước to nhỏ khác nhau gợi nên những hình có mối liên hệ đồng dạng với nhau.

I. Phép đồng dạng phối cảnh (Phép vị tự)

Hoạt động 1 trang 26 Chuyên đề Toán lớp 11: Trong mặt phẳng cho điểm O. Với mỗi điểm M trong mặt phẳng, hãy xác định điểm M' sao cho $\vec{O M'} = 2 \vec{O M}$ (Hình 47).

Chuyên đề Toán 11 (Cánh diều) Bài 2: Phép đồng dạng (ảnh 2)

Lời giải:

Cách xác định:

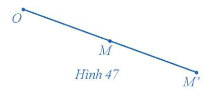
- Lấy điểm O và điểm M bất kì;

- Trên tia OM, lấy điểm M' sao cho OM' = 2OM.

Khi đó ta có $\vec{O M'} = 2 \vec{O M}$ (tham khảo Hình 47).

Luyện tập 1 trang 27 Chuyên đề Toán lớp 11: Cho tam giác ABC có O là trung điểm của cạnh BC. Xác định ảnh của tam giác ABC trong phép vị tự tâm O tỉ số $k = \frac{1}{2}$ .

Lời giải:

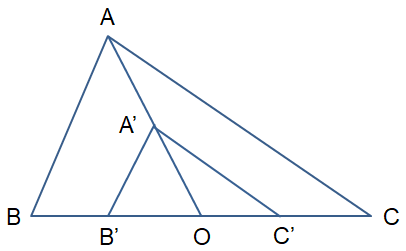
Chuyên đề Toán 11 (Cánh diều) Bài 2: Phép đồng dạng (ảnh 3)

Gọi A', B', C' lần lượt là ảnh của A, B, C qua phép vị tự tâm O tỉ số $k = \frac{1}{2}$ . Khi đó ta có:

$\vec{O A'} = \frac{1}{2} \vec{O A}; \vec{O B'} = \frac{1}{2} \vec{O B}; \vec{O C'} = \frac{1}{2} \vec{O C}$ .

Do đó, các điểm A', B', C' lần lượt là trung điểm của OA, OB, OC.

Vậy ảnh của tam giác ABC trong phép vị tự tâm O tỉ số $k = \frac{1}{2}$ là tam giác A'B'C' với A', B', C' lần lượt là trung điểm của OA, OB, OC.

Hoạt động 2 trang 27 Chuyên đề Toán lớp 11: Cho phép vị tự tâm O tỉ số k và hai điểm A, B. Giả sử A' = V_{(O, k)}(A), B' = V_{(O, k)}(B).

a) Biểu diễn các vectơ $\vec{O A'}, \vec{O B'}$ lần lượt theo các vectơ $\vec{O A}, \vec{O B}$ .

b) Biểu diễn các vectơ $\vec{A' B'}$ theo vectơ $\vec{A B}$ . Từ đó, tìm mối liên hệ độ dài giữa hai đoạn thẳng A'B' và AB.

Lời giải:

a) Vì A' = V_{(O, k)}(A), B' = V_{(O, k)}(B) nên $\vec{O A'} = k \vec{O A}, \vec{O B'} = k \vec{O B}$ .

b) Ta có: $\vec{A' B'} = \vec{O B'} - \vec{O A'} = k \vec{O B} - k \vec{O A} = k (\vec{O B} - \vec{O A}) = k \vec{A B}$ (theo quy tắc hiệu).

Vậy $\vec{A' B'} = k \vec{A B}$ , từ đó suy ra A'B' = |k|AB.

Hoạt động 3 trang 28 Chuyên đề Toán lớp 11: Cho phép vị tự tâm O tỉ số k và ba điểm A, B, C thẳng hàng sao cho B nằm giữa A và C. Giả sử A' = V_{(O, k)}(A), B' = V_{(O, k)}(B), C' = V_{(O, k)}(C).

a) Biểu diễn các vectơ $\vec{B' A'}, \vec{B' C'}$ lần lượt theo các vectơ $\vec{B A}, \vec{B C}$ .

b) Hai vectơ $\vec{B A}$ và $\vec{B C}$ có ngược hướng không?

c) Hai vectơ $\vec{B' A'}$ và $\vec{B' C'}$ có ngược hướng không? Từ đó, nêu mối quan hệ giữa ba điểm A', B', C'.

Lời giải:

a) Vì A' = V_{(O, k)}(A), B' = V_{(O, k)}(B), C' = V_{(O, k)}(C) nên $\vec{B' A'} = k \vec{B A}$ và $\vec{B' C'} = k \vec{B C}$ .

b) Vì A, B, C thẳng hàng và B nằm giữa A và C nên hai vectơ $\vec{B A}$ và $\vec{B C}$ ngược hướng với nhau.

c) +) Với k > 0, ta có:

$\vec{B' A'} = k \vec{B A}$ nên hai vectơ $\vec{B' A'}$ và $\vec{B A}$ cùng hướng với nhau.

$\vec{B' C'} = k \vec{B C}$ nên hai vectơ $\vec{B' C'}$ và $\vec{B C}$ cùng hướng với nhau.

Mà hai vectơ $\vec{B A}$ và $\vec{B C}$ ngược hướng với nhau nên hai vectơ $\vec{B' A'}$ và $\vec{B' C'}$ ngược hướng với nhau.

+) Với k < 0, ta có:

$\vec{B' A'} = k \vec{B A}$ nên hai vectơ $\vec{B' A'}$ và $\vec{B A}$ ngược hướng với nhau.

$\vec{B' C'} = k \vec{B C}$ nên hai vectơ $\vec{B' C'}$ và $\vec{B C}$ ngược hướng với nhau.

Mà hai vectơ $\vec{B A}$ và $\vec{B C}$ ngược hướng với nhau nên hai vectơ và ngược hướng với nhau.

Từ đó suy ra với k ≠ 0 thì hai vectơ null và $\vec{B' C'}$ ngược hướng với nhau.

Do đó, ba điểm A', B', C' thẳng hàng và B' nằm giữa hai điểm A' và C'.

Luyện tập 2 trang 30 Chuyên đề Toán lớp 11: Cho đường tròn (C) có tâm O bán kính R. Xác định ảnh của đường tròn (C) qua phép vị tự tâm O tỉ số $k = - \frac{1}{2}$ .

Lời giải:

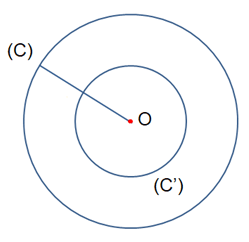
Chuyên đề Toán 11 (Cánh diều) Bài 2: Phép đồng dạng (ảnh 4)

Qua phép vị tự tâm O tỉ số $k = - \frac{1}{2}$ thì điểm O biến thành chính nó. Do đó, ảnh của đường tròn (C) là đường tròn (C') có tâm O và bán kính R' = $|- \frac{1}{2}|$ R = $\frac{1}{2}$ R.

II. Phép đồng dạng

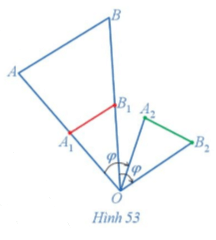
Hoạt động 4 trang 30 Chuyên đề Toán lớp 11: Trong Hình 53, cho đoạn thẳng AB. Nêu cách dựng:

a) Đoạn thẳng A₁B₁ là ảnh của đoạn thẳng AB qua phép vị tự tâm O tỉ số $\frac{1}{2}$ ;

b) Đoạn thẳng A₂B₂ là ảnh của đoạn thẳng A₁B₁ qua phép quay tâm O với góc quay φ = – 60°.

c) Nhận xét về mối liên hệ giữa độ dài các đoạn thẳng AB, A₂B₂.

Chuyên đề Toán 11 (Cánh diều) Bài 2: Phép đồng dạng (ảnh 5)

Lời giải:

a) Nối O với A và O với B, lấy điểm A₁ là trung điểm của đoạn thẳng OA, lấy điểm B₁ là trung điểm của đoạn thẳng OB. Khi đó $\vec{O A_{1}} = \frac{1}{2} \vec{O A}, \vec{O B_{1}} = \frac{1}{2} \vec{O B}$ .

Do đó, A₁, B₁ tương ứng là ảnh của A, B qua phép vị tự tâm O tỉ số $\frac{1}{2}$ nên đoạn thẳng A₁B₁ là ảnh của đoạn thẳng AB qua phép vị tự tâm O tỉ số $\frac{1}{2}$ .

b) Phép quay với góc quay φ = – 60° có chiều quay cùng chiều kim đồng hồ.

Theo chiều quay cùng chiều kim đồng hồ, dựng góc $\hat{A_{1} O A_{2}} = 60 °$ sao cho OA₁ = OA₂; dựng góc $\hat{B_{1} O B_{2}} = 60 °$ sao cho OB₁ = OB₂. Khi đó ta có A₂, B₂ tương ứng là ảnh của A₁, B₁ qua phép quay tâm O với góc quay φ = – 60° nên đoạn thẳng A₂B₂ là ảnh của đoạn thẳng A₁B₁ qua phép quay tâm O với góc quay φ = – 60°.

c) Vì đoạn thẳng A₁B₁ là ảnh của đoạn thẳng AB qua phép vị tự tâm O tỉ số $\frac{1}{2}$ nên $A_{1} B_{1} = \frac{1}{2} A B$ .

Vì đoạn thẳng A₂B₂ là ảnh của đoạn thẳng A₁B₁ qua phép quay tâm O với góc quay φ = – 60° nên A₂B₂ = A₁B₁.

Từ đó suy ra A₂B₂ = $\frac{1}{2}$ AB.

Luyện tập 3 trang 31 chuyên đề Toán lớp 11: Người ta dùng một kính hiển vi có khả năng phóng to vật lên gấp 100 000 lần để quan sát một virus và đo được kích thước của virus là 2 mm. Hỏi kích thước thật của virus là bao nhiêu micromét (μm)?

Lời giải:

Kích thước thật của virus là

2 : 100 000 = 0,00002 (mm) = 0,02 (μm).

Hoạt động 5 trang 31 chuyên đề Toán lớp 11: Quan sát Hình 54 và cho biết:

a) Hình chữ nhật A"B"C"D" nhận được từ hình chữ nhật ABCD bằng cách nào.

b) Hình chữ nhật A'B'C'D' nhận được từ hình chữ nhật A"B"C"D" bằng cách nào.

c) Phép đồng dạng nào biến hình chữ nhật ABCD thành hình chữ nhật A'B'C'D'.

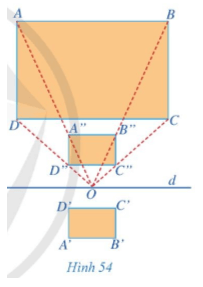
Chuyên đề Toán 11 (Cánh diều) Bài 2: Phép đồng dạng (ảnh 6)

Lời giải:

a) Áp dụng định lí Thales, ta có:

A"B" // AB nên $\frac{O A "}{O A} = \frac{O B "}{O B}$

B"C" // BC nên $\frac{O B "}{O B} = \frac{O C "}{O C}$

C"D" // CD nên $\frac{O C "}{O C} = \frac{O D "}{O D}$

D"A" // DA nên $\frac{O D "}{O D} = \frac{O A "}{O A}$ .

Từ đó suy ra $\frac{O A "}{O A} = \frac{O B "}{O B} = \frac{O C "}{O C} = \frac{O D "}{O D} = k$ với k ≠ 0.

Do đó, $\vec{O A "} = k \vec{O A}, \vec{O B "} = k \vec{O B}, \vec{O C "} = k \vec{O C}, \vec{O D "} = k \vec{O D}$ nên ta có A", B", C", D" lần lượt là ảnh của A, B, C, D qua phép vị tự tâm O, tỉ số k. Như vậy, hình chữ nhật A"B"C"D" nhận được từ hình chữ nhật ABCD qua phép vị tự tâm O tỉ số k với k = $\frac{O A "}{O A}$ .

b) Qua phép đối xứng trục d, các điểm A", B", C", D" biến thành các điểm A', B', C', D'.

Do đó, hình chữ nhật A'B'C'D' nhận được từ hình chữ nhật A"B"C"D" qua phép đối xứng trục d.

c) Phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k với k = $\frac{O A "}{O A}$ và phép đối xứng trục d (V_{(O, k)} trước, Đ_d sau) biến hình chữ nhật ABCD thành hình chữ nhật A'B'C'D'.

Luyện tập 4 trang 32 chuyên đề Toán lớp 11: Trong Ví dụ 8, chứng minh rằng hai hình OMGE và COEN đồng dạng với nhau.

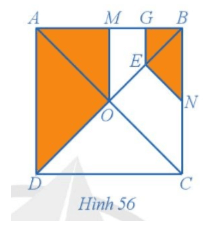
Chuyên đề Toán 11 (Cánh diều) Bài 2: Phép đồng dạng (ảnh 7)

Lời giải:

Chuyên đề Toán 11 (Cánh diều) Bài 2: Phép đồng dạng (ảnh 8)

+) Vì O là giao hai đường chéo của hình vuông ABCD nên AC và BD vuông góc với nhau tại O và O là trung điểm của AC và BD, lại có AC = BD nên suy ra OA = OB = OC = OD.

Tam giác OBC cân tại O (OB = OC) có ON là đường trung tuyến nên ON là đường phân giác, suy ra $\hat{C O N} = \hat{B O N} = \frac{\hat{B O C}}{2} = \frac{90 °}{2} = 45 °$ .

Tương tự ta chứng minh được $\hat{B O M} = 45 °$ hay $\hat{E O M} = 45 °$ .

Trên tia ON, lấy điểm C' sao cho OC' = OC. Trên tia OB, lấy điểm N' sao cho ON' = ON. Trên tia OM, lấy điểm E' sao cho OE' = OE.

Lại có $\hat{C O C'} = \hat{C O N} = 45 °$ , $\hat{N O N'} = \hat{B O N} = 45 °$ và $\hat{N O N'} = \hat{B O N} = 45 °$ .

Mà phép quay với góc quay 45° có chiều quay ngược chiều kim đồng hồ.

Do đó, ta có phép quay tâm O với góc quay 45° biến các điểm C, O, E, N tương ứng thành các điểm C'¸O, E', N' nên phép quay tâm O với góc quay 45° biến hình COEN thành hình C'OE'N' (1).

+) Giả sử hình vuông ABCD có cạnh là a.

Khi đó BD = AC = a $\sqrt{2}$ , OB = OC = $\frac{a \sqrt{2}}{2}$ , ON = $\frac{A B}{2} = \frac{a}{2}$ .

Suy ra $O E = \frac{O B}{2} = \frac{a \sqrt{2}}{4}$ , OC' = OC = $\frac{a \sqrt{2}}{2}$ , ON' = ON = $\frac{a}{2}$ .

Suy ra $\frac{O E}{O N'} = \frac{\sqrt{2}}{2}, \frac{O N}{O C'} = \frac{\sqrt{2}}{2}$ , do đó $\frac{O E}{O N'} = \frac{O N}{O C'} = \frac{\sqrt{2}}{2}$ .

Qua E, kẻ đường thẳng song song với E'N' cắt OM tại F, suy ra EF // E'N' nên theo định lí Thales trong tam giác OE'N' ta có $\frac{O F}{O E'} = \frac{O E}{O N'} = \frac{\sqrt{2}}{2}$ .

Từ đó suy ra $\frac{O N}{O C'} = \frac{O E}{O N'} = \frac{O F}{O E'} = \frac{\sqrt{2}}{2}$ nên $\vec{O N} = \frac{\sqrt{2}}{2} \vec{O C'}$ , $\vec{O E} = \frac{\sqrt{2}}{2} \vec{O N'}$ , $\vec{O F} = \frac{\sqrt{2}}{2} \vec{O E'}$ .

Như vậy, ta có phép vị tự tâm O với tỉ số $\frac{\sqrt{2}}{2}$ biến các điểm C'¸O, E', N' tương ứng thành các điểm N, O, F, E hay phép vị tự tâm O với tỉ số $\frac{\sqrt{2}}{2}$ biến hình C'OE'N' thành hình NOFE (2).

+) Tam giác NOB vuông cân tại N có NE là đường trung tuyến nên NE cũng là đường cao và NE = $\frac{O B}{2}$ = OE, suy ra $\hat{N E O} = 90 °$ và EN = EO.

Tương tự, ta chứng minh được $\hat{M E O} = 90 °$ và EM = EO.

Ta chứng minh được EFMG là hình vuông nên $\hat{F E G} = 90 °$ và EF = EG.

Mà phép quay với góc quay – 90° có chiều quay cùng chiều kim đồng hồ.

Do đó, ta có phép quay tâm E với góc quay – 90° biến các điểm N, O, F, E tương ứng thành các điểm O, M, G, E hay phép quay tâm E với góc quay – 90° biến hình NOFE thành hình OMGE (3).

Từ (1), (2) và (3) suy ra hai hình OMGE và COEN đồng dạng với nhau.

Bài tập

Bài 1 trang 32 Chuyên đề Toán 11: Phép biến hình nào trong các phép biến hình dưới đây là phép vị tự?

a) Phép tịnh tiến theo vectơ khác $\vec{0}$ ;

b) Phép đối xứng tâm;

c) Phép đối xứng trục;

d) Phép quay.

Lời giải:

a) Phép tịnh tiến theo vectơ khác $\vec{0}$ không phải là phép vị tự vì không có điểm nào biến thành chính nó.

b) Phép đối xứng tâm là phép vị tự với tâm là tâm đối xứng và tỉ số k = – 1.

Chứng minh:

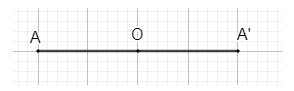
Chuyên đề Toán 11 (Cánh diều) Bài 2: Phép đồng dạng (ảnh 9)

Giả sử ta có phép đối xứng tâm O biến điểm A thành điểm A', khi đó O là trung điểm của AA', suy ra $\vec{O A'} = - \vec{O A}$ , do đó ta có phép vị tự tâm O tỉ số – 1 biến điểm A thành A'.

c) Phép đối xứng trục không phải là phép vị tự vì các đường thẳng nối cặp điểm tương ứng không đồng quy.

d) Phép quay với tâm O bất kì và góc quay φ = 2kπ (chính là phép đồng nhất) là phép vị tự tâm O với tỉ số k = 1.

Phép quay với tâm O bất kì và góc quay φ = (2k + 1)π (chính là phép đối xứng tâm O) là phép vị tự tâm O với tỉ số k = – 1.

Phép quay với góc bất kì khác 2kπ, (2k + 1)π không phải là phép vị tự.

Bài 2 trang 32 Chuyên đề Toán 11: Phép biến hình nào trong các phép biến hình dưới đây không là phép đồng dạng?

a) Phép đối xứng trục;

b) Phép đồng nhất;

c) Phép vị tự tỉ số k = 1;

d) Phép biến hình biến mỗi điểm trong mặt phẳng thành điểm A cho trước.

Lời giải:

a) Phép đối xứng trục là phép đồng dạng tỉ số 1.

b) Phép đồng nhất là phép đồng dạng tỉ số 1.

c) Phép vị tự tỉ số k = 1 là phép đồng dạng tỉ số |k| = |1| = 1.

d) Phép biến hình biến mỗi điểm trong mặt phẳng thành điểm A cho trước không phải là phép đồng dạng.

Thật vậy, với hai điểm B, C phân biệt, ta có A là ảnh của B và cũng là ảnh của C qua phép biến hình đó. Ta có BC ≠ 0 (do hai điểm phân biệt), AA = 0, do đó không tồn tại số k > 0 để BC = kAA, vậy phép biến hình đã cho không phải phép đồng dạng.

Bài 3 trang 32 Chuyên đề Toán 11: Khẳng định nào dưới đây là đúng?

a) Hai tam giác luôn đồng dạng với nhau;

b) Hai hình chữ nhật luôn đồng dạng với nhau;

c) Hai hình thoi luôn đồng dạng với nhau;

d) Hai hình vuông luôn đồng dạng với nhau.

Lời giải

+ Khẳng định a) và b) sai.

- Ta có thể lấy hai tam giác với các kích thước là (3; 4; 5) và (6; 7; 8), ta thấy tỉ lệ các cặp cạnh tương ứng không bằng nhau. Do đó hai tam giác bất kì không đồng dạng với nhau.

- Tương tự, hai hình chữ nhật bất kì cũng không đồng dạng với nhau.

+ Khẳng định c) và d) đúng.

Vì hình thoi và hình vuông đều là các hình có 4 cạnh bằng nhau.

Bài 4 trang 32 Chuyên đề Toán 11: Trên bản đồ bay với tỉ lệ xích 1: 10 000 000, khoảng cách giữa Hà Nội và Tokyo đo được là 37,34 cm. Khoảng cách thực tế (tính theo đường chim bay) giữa Hà Nội và Tokyo là bao nhiêu kilômét?

Lời giải:

Khoảng cách thực tế (tính theo đường chim bay) giữa Hà Nội và Tokyo là

37,34 . 10 000 000 = 373 400 000 (cm) = 3 734 (km).

Bài 5 trang 33 Chuyên đề Toán 11: >Một thấu kính phân kì có tiêu cự OF = OF' = 20 cm (kính cận). Vật sáng AB được đặt vuông góc với trục chính của thấu kính, cách thấu kính một đoạn OA = 60 cm, qua thấu kính cho ảnh ảo A'B' (Hình 57). A'B' là ảnh của AB qua một phép vị tự tâm O tỉ số k.

Tính khoảng cách A'O từ ảnh đến thấu kính và so sánh khoảng cách đó với khoảng cách AO từ vật đến thấu kính.

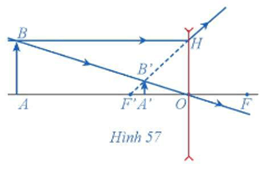
Chuyên đề Toán 11 (Cánh diều) Bài 2: Phép đồng dạng (ảnh 10)

Lời giải:

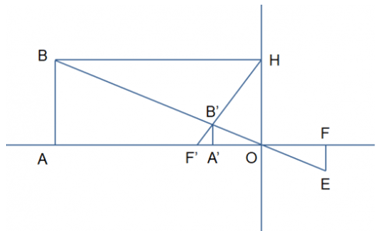
Chuyên đề Toán 11 (Cánh diều) Bài 2: Phép đồng dạng (ảnh 11)

Từ F, kẻ EF // AB // A'B' (F thuộc đường thẳng OB).

Ta có BH = OA = 60 cm.

Vì OF' // BH nên $\frac{O B'}{B B'} = \frac{O F'}{B H} = \frac{20}{60} = \frac{1}{3}$ (định lí Thales). Suy ra $O B' = \frac{1}{4} O B$ .

Vì A'B' // AB nên $\frac{A' B'}{A B} = \frac{O B'}{O B} = \frac{1}{4}$ AB (1).

Vì AB // EF nên $\frac{E F}{A B} = \frac{O F}{O A} = \frac{20}{60} = \frac{1}{3}$ (định lí Thales). Suy ra EF = $\frac{1}{3}$ AB (2).

Từ (1) và (2) suy ra $\frac{A' B'}{E F} = \frac{3}{4}$ .

Vì A'B' // EF nên $\frac{O A'}{O F} = \frac{A' B'}{E F} = \frac{3}{4}$ (định lí Thales).

Do đó OA' = $\frac{3}{4}$ OF = $\frac{3}{4}$ . 20 = 15 (cm).

Ta có: $\frac{O A'}{O A} = \frac{15}{60} = \frac{1}{4}$ , suy ra OA' = $\frac{1}{4}$ OA.

Bài 6 trang 33 Chuyên đề Toán 11: Chứng minh rằng qua phép vị tự tâm O tỉ số k (k ≠ 0), ảnh của mọi đường thẳng đi qua tâm O là chính nó.

Lời giải:

Theo định lí về tính chất của phép vị tự ta có: Phép vị tự tâm O tỉ số k (k ≠ 0) biến đường thẳng thành đường thẳng song song hoặc trùng với nó.

Giả sử qua phép vị tự tâm O tỉ số k (k ≠ 0) biến đường thẳng d thành đường thẳng d' thì d // d' hoặc d ≡ d'.

Mà O cố định, O thuộc đường thẳng d (giả thiết) và phép vi tự tâm O tỉ số k (k ≠ 0) biến điểm O thành chính nó nên O cũng thuộc đường thẳng d'. Do đó, d và d' không thể song song với nhau nên d và d' trùng nhau.

Như vậy, phép vị tự tâm O tỉ số k (k ≠ 0) biến đường thẳng d thành đường thẳng trùng với chính nó.

Nói cách khác: Qua phép vị tự tâm O tỉ số k (k ≠ 0), ảnh của mọi đường thẳng đi qua tâm O là chính nó.

Bài 7 trang 33 Chuyên đề Toán 11: Cho tam giác nhọn ABC có trực tâm H. Xác định ảnh của tam giác ABC qua phép vị tự tâm H tỉ số k = $\frac{1}{2}$ .

Lời giải:

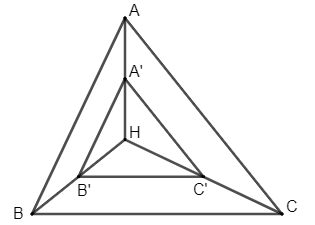
Chuyên đề Toán 11 (Cánh diều) Bài 2: Phép đồng dạng (ảnh 12)

Gọi A', B', C' lần lượt là ảnh của A, B, C qua phép vị tự tâm H tỉ số k = $\frac{1}{2}$ .

Khi đó ta có: $\vec{H A'} = \frac{1}{2} \vec{H A}; \vec{H B'} = \frac{1}{2} \vec{H B}; \vec{H C'} = \frac{1}{2} \vec{H C}$ .

Từ đó suy ra A', B', C' lần lượt là trung điểm của AH, BH, CH.

Vậy ảnh của tam giác ABC qua phép vị tự tâm H tỉ số k = $\frac{1}{2}$ là tam giác A'B'C' với A', B', C' lần lượt là trung điểm của AH, BH, CH.

Bài 8 trang 33 Chuyên đề Toán 11: Cho hai đường tròn (O₁; R) và (O₂; 2R) tiếp xúc ngoài với nhau tại điểm A. Tìm phép vị tự biến đường tròn (O₁; R) thành đường tròn (O₂; 2R).

Lời giải:

Chú ý: Phép vị tự biến đường tròn có bán kính R thành đường tròn có bán kính R' = |k|R và có tâm là ảnh của tâm.

Hai đường tròn (O₁; R) và (O₂; 2R) tiếp xúc ngoài với nhau tại điểm A và đường tròn tâm O₂ có bán kính gấp 2 lần đường tròn tâm O₁.

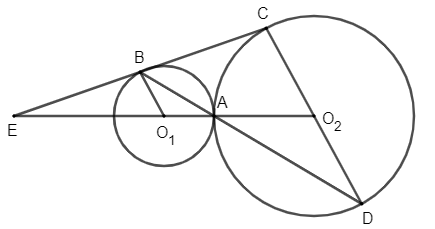
Chuyên đề Toán 11 (Cánh diều) Bài 2: Phép đồng dạng (ảnh 13)

- Trên đường tròn (O₁; R) lấy điểm B bất kì.

- Trên đường tròn (O₂; 2R) dựng đường kính CD // O₁B.

- BC cắt O₁O₂ tại E.

+) Ta có: O₁B // CO₂ nên theo định lí Thales có $\frac{E O_{2}}{E O_{1}} = \frac{O_{2} C}{O_{1} B} = \frac{2 R}{R} = 2$ .

Suy ra $\vec{E O_{2}} = 2 \vec{E O_{1}}$ nên ta có phép vị tự tâm E, tỉ số 2 biến điểm O₁ thành điểm O₂.

Như vậy, phép vị tự tâm E, tỉ số 2 biến đường tròn (O₁; R) thành đường tròn (O₂; 2R).

+) Nối B với D, ta chứng minh được BD cắt O₁O₂ tại điểm tiếp xúc A của hai đường tròn.

Ta có: $\frac{A O_{2}}{A O_{1}} = \frac{2 R}{R} = 2$ và A nằm giữa hai điểm O₁ và O₂ nên $\vec{A O_{2}} = - 2 \vec{A O_{1}}$ . Do đó, ta có phép vị tự tâm A, tỉ số – 2 biến điểm O₁ thành điểm O₂.

Như vậy, phép vị tự tâm A, tỉ số – 2 biến đường tròn (O₁; R) thành đường tròn (O₂; 2R).

Vậy có 2 phép vị tự biến đường tròn (O₁; R) thành đường tròn (O₂; 2R).

Bài 9 trang 33 Chuyên đề Toán 11: Chứng minh rằng nếu phép đồng dạng F biến tam giác ABC thành tam giác A'B'C' thì F biến trọng tâm, trực tâm, tâm đường tròn ngoại tiếp tam giác ABC thành trọng tâm, trực tâm, tâm đường tròn ngoại tiếp tam giác A'B'C'.

Lời giải:

+) Gọi D là trung điểm của đoạn thẳng BC thì phép đồng dạng F biến điểm D thành trung điểm D' của đoạn thẳng B'C' và vì thế trung tuyến AD của tam giác ABC biến thành trung tuyến A'D' của tam giác A'B'C'. Đối với hai trung tuyến còn lại cũng vậy. Vì trọng tâm tam giác là giao điểm của các đường trung tuyến nên trọng tâm tam giác ABC biến thành trọng tâm tam giác A'B'C'.

+) Gọi AH là đường cao của tam giác ABC (H ∈ BC). Khi đó phép đồng dạng F biến đường thẳng AH thành đường thẳng A'H'. Vì AH ⊥ BC nên A'H' ⊥ B'C', nói cách khác A'H' là đường cao của tam giác A'B'C'. Đối với các đường cao khác cũng thế. Vì trực tâm tam giác là giao điểm của các đường cao nên trực tâm tam giác ABC biến thành trực tâm tam giác A'B'C'.

+) Gọi O là tâm đường tròn ngoại tiếp của tam giác ABC thì OA = OB = OC nên nếu điểm O biến thành điểm O' thì O'A' = O'B' = O'C' = kOA = kOB = kOC, do đó O' là tâm đường tròn ngoại tiếp tam giác A'B'C'.

Bài 10 trang 33 Chuyên đề Toán 11: Chứng minh rằng các đa giác đều có cùng số cạnh thì đồng dạng với nhau.

Lời giải:

Giả sử cho hai n-giác đều A₁A₂...A_n và B₁B₂…B_n có tâm lần lượt là O và O'. Đặt $k = \frac{B_{1} B_{2}}{A_{1} A_{2}} = \frac{O' B_{1}}{O A_{1}}$ . Gọi V là phép vị tự tâm O, tỉ số k và C₁C₂…C_n là ảnh của đa giác A₁A₂…A_n qua phép vị tự V. Hiển nhiên C₁C₂…C_n cũng là đa giác đều và vì $\frac{C_{1} C_{2}}{A_{1} A_{2}} = k$ nên C₁C₂ = B₁B₂. Vậy hai n-giác đều C₁C₂….C_n và B₁B₁…B_n có cạnh bằng nhau, tức là có phép dời hình D biến C₁C₂…C_n thành B₁B₂…B_n. Nếu gọi F là phép hợp thành của V và D thì F là phép đồng đạng biến A₁A₂…A_n thành B₁B₂…B_n. Vậy hai đa giác đều đó đồng dạng với nhau.

Bài 11 trang 33 Chuyên đề Toán 11: Cho hình vuông ABCD có hai đường chéo cắt nhau tại O. Gọi M, N, E lần lượt là trung điểm của AB, BC, BO (Hình 58). Chứng minh rằng hai hình AMOD và OENC đồng dạng với nhau.

Chuyên đề Toán 11 (Cánh diều) Bài 2: Phép đồng dạng (ảnh 14)

Lời giải:

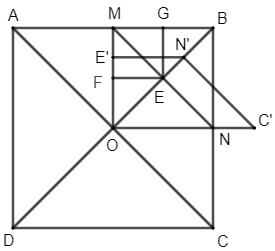
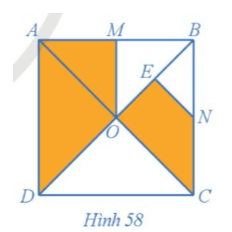
Gọi G là trung điểm của BM.

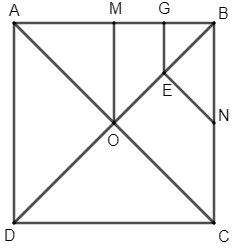
Chuyên đề Toán 11 (Cánh diều) Bài 2: Phép đồng dạng (ảnh 15)

Khi đó, ta thấy Hình 58 và Hình 56 là hai hình giống nhau.

+) Theo kết quả Ví dụ 8 trang 32 thì hai hình BGEN và AMOD đồng dạng với nhau (1).

+) Theo kết quả Luyện tập 4 trang 32 thì hai hình OMGE và COEN đồng dạng với nhau hay hai hình MGEO và OENC đồng dạng với nhau (2).

+) Thực hiện phép đối xứng trục GE thì hình BGEN biến thành hình MGEO (3).

Do đó, hai hình BGEN và MGEO đồng dạng với nhau.

Từ (1), (2) và (3) suy ra hai hình AMOD và OENC đồng dạng với nhau.

Bài 12 trang 33 Chuyên đề Toán 11: Hình 59 mô tả một viên gạch trang trí hình tam giác đều. Chứng minh rằng hình hoa ba cánh màu xanh và hình hoa ba cánh màu đỏ đồng dạng với nhau.

Chuyên đề Toán 11 (Cánh diều) Bài 2: Phép đồng dạng (ảnh 16)

Lời giải:

Gọi viên gạch trang trí là ABC, giao của các canh hoa màu đỏ với BC, CA, AB lần lượt là các điểm D, E, F, G là tâm của hình tam giác đều, khi đó G là tâm của các hình hoa (quan sát hình vẽ dưới đây).

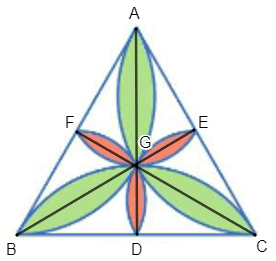
Chuyên đề Toán 11 (Cánh diều) Bài 2: Phép đồng dạng (ảnh 17)

Qua phép quay tâm G, góc quay 120° hình cánh hoa màu xanh đỉnh A biến thành hình cánh hoa màu xanh đỉnh B, hình cánh hoa màu xanh đỉnh B biến thành hình cánh hoa màu xanh đỉnh C, hình cánh hoa màu đỏ đỉnh F biến thành hình cánh hoa màu đỏ đỉnh D, hình cánh hoa màu đỏ đỉnh D biến thành hình cánh hoa màu đỏ đỉnh E. Do đó, các hình cánh hoa màu xanh đồng dạng với nhau theo tỉ số 1 và các hình cánh hoa màu đỏ đồng dạng với nhau theo tỉ số 1 (phép dời hình là phép đồng dạng tỉ số 1).

Do đó, GA = GB = GC và GD = GE = GF.

Ta có G là tâm của hình tam giác đều ABC nên G cũng là trọng tâm của tam giác ABC và D, E, F lần lượt là trung điểm của BC, CA, AB. Khi đó ta có: $\vec{G D} = - \frac{1}{2} \vec{G A}, \vec{G E} = - \frac{1}{2} \vec{G B}$ và $\vec{G F} = - \frac{1}{2} \vec{G C}$ . Do đó, D, E, F lần lượt là ảnh của A, B, C qua phép vị tự tâm G, tỉ số $- \frac{1}{2}$ . Như vậy, khi ta lấy mỗi điểm bất kì trên hình hoa ba cánh màu xanh thì qua phép vị tự tâm G, tỉ số, điểm đó đều biến thành một điểm tương ứng trên hình hoa ba cánh màu đỏ. Vậy có phép đồng dạng biến hình hoa ba cánh màu xanh thành hình hoa ba cánh màu đỏ. Do đó, rằng hình hoa ba cánh màu xanh và hình hoa ba cánh màu đỏ đồng dạng với nhau.