Mở đầu trang 41 Chuyên đề Toán 11: Trong lí thuyết đồ thị, bài toán Bảy câu cầu ở Königsberg (nay là thành phố Kaliningrad, nước Nga) được phát biểu như sau: Thành phố có 7 cây cầu bắc qua sông như Hình 2.15a dưới đây, có thể nào đi dạo qua khắp các cây cầu nhưng mỗi cầu chỉ đi qua một lần không?

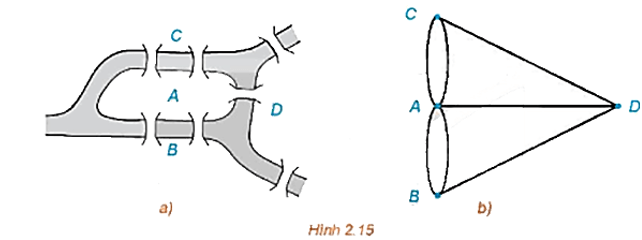
Nếu ta coi mỗi khu vực A, B, C, D của thành phố là một đỉnh, mỗi cầu qua lại hai khu vực như một cạnh nối hai đỉnh, thì bản đồ thành phố Königsberg là một đa đồ thị như Hình 2.15b. Vấn đề đặt ra chính là: Có thể vẽ được Hình 2.15b bằng một nét liền hay không?

Lời giải:

Sau bài học này, ta sẽ giải quyết được bài toán trên như sau:

Xét đa đồ thị G ở Hình 2.15b. Vì các đỉnh A, B, C, D đều có bậc lẻ nên theo Định lí 2, G không có đường đi Euler và không có cả chu trình Euler.

Vậy không thể nào đi dạo qua khắp các cây cầu của thành phố Königsberg mà mỗi cầu chỉ đi qua một lần.

1. Đường đi Euler

HĐ1 trang 41 Chuyên đề Toán 11: Nhận biết đường đi Euler

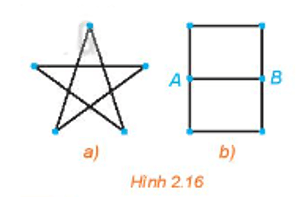
Hãy thử vẽ mỗi hình trên Hình 2.16 bằng một nét liền.

Lời giải:

Ta có thể vẽ mỗi hình trên Hình 2.16 bằng một nét liền.

- Đối với Hình 2.16 a), ta có thể vẽ một nét liền theo thứ tự 123451.

- Đối với Hình 2.16 b), ta có thể vẽ một nét liền theo thứ tự ABCDAEFB.

Luyện tập 1 trang 41 Chuyên đề Toán 11: Đồ thị nào dưới đây có một đường đi Euler? Hãy chỉ ra một đường đi Euler của nó.

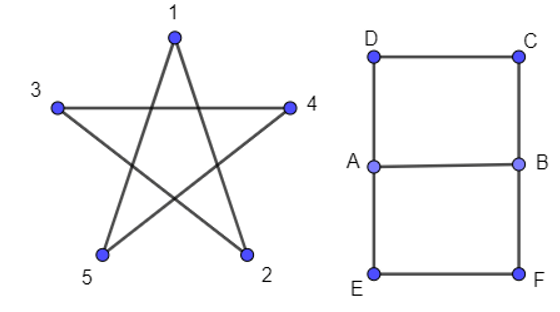
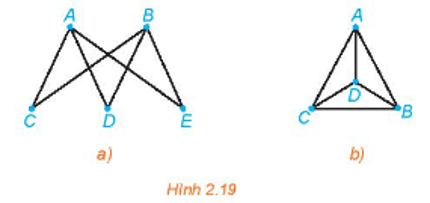
Lời giải:

- Đồ thị Hình 2.19a có đường đi Euler từ A đến B vì đồ thị này liên thông và các đỉnh A, B có bậc 3 (bậc lẻ), còn các đỉnh C, D, E đều có bậc 2 (bậc chẵn). Một đường đi Euler của đồ thị này là ACBDAEB.

- Đồ thị Hình 2.19b không có đường đi Euler vì đồ thị này có bốn đỉnh bậc lẻ (ở đây là bậc bằng 3).

2. Đường đi Hamilton

HĐ2 trang 43 Chuyên đề Toán 11: Nhận biết đường đi Hamilton

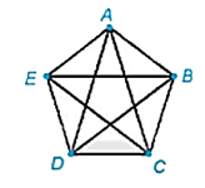
Có 5 thành phố du lịch A, B, C, D, E và các con đường nối các thành phố này như Hình 2.20. Hãy chỉ ra một cách để đi tham quan cả 5 thành phố đó, mà không cần đến địa điểm nào quá một lần.

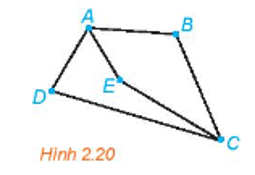
Lời giải:

Một cách để đi tham quan cả 5 thành phố đó, mà không cần đến địa điểm nào quá một lần là ta có thể đi theo thứ tự EABCD (hoặc có thể chọn ECBAD, hoặc BADCE,...).

Luyện tập 2 trang 44 Chuyên đề Toán 11: Đồ thị nào trong Hình 2.2.3 có đường đi Hamilton? Hãy chỉ ra một đường đi Hamiton của nó.

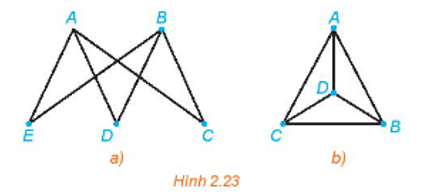
Lời giải:

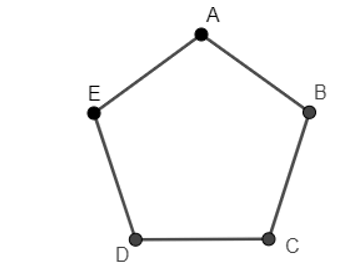
- Đồ thị Hình 2.23 a) có 5 đỉnh, trong đó đỉnh A và B đều có bậc 3, các đỉnh còn lại E, D, C đều có bậc 2 nên mỗi đỉnh đều có bậc không nhỏ hơn $\frac{5-1}{2}=\frac{4}{2}=2$. Do đó, theo định lí 4 (suy ra từ định lí Dirac), đồ thị này có đường đi Hamilton. Một đường đi Hamilton của đồ thị này là CBDAE.

- Đồ thị Hình 2.23 b) có 4 đỉnh, mỗi đỉnh đều có bậc là 3 nên mỗi cặp đỉnh không kề nhau bất kì đều có tổng bậc là 3 + 3 = 6 > 4. Do đó, theo định lí Ore, đồ thị này có một chu trình Hamilton nên nó có đường đi Hamilton. Một đường đi Hamilton của đồ thị này là ABCD.

Bài tập

Bài 2.7 trang 44 Chuyên đề Toán 11: Mỗi đồ thị sau có một chu trình Euler hoặc một chu trình Hamilton hay không? Hãy vẽ một chu trình Euler hoặc một chu trình Hamilton khi có thể.

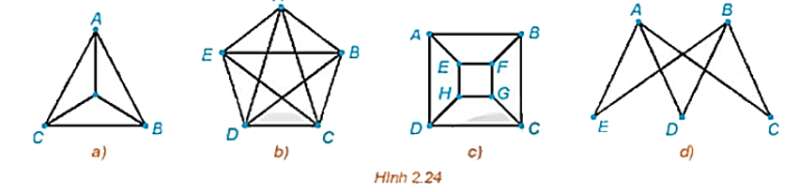
Lời giải:

+) Đồ thị Hình 2.24 a) có các đỉnh đều có bậc là 3 nên theo định lí Euler đồ thị này không có chu trình Euler.

Lại có đồ thị a) có 4 đỉnh, tổng số bậc của hai đỉnh không kề nhau luôn không nhỏ hơn 4 nên theo định lí Ore, đồ thị a) có một chu trình Hamilton.

Một chu trình Hamiltol của đồ thị a) là ABCDA.

+) Đồ thị Hình 2.24 b) liên thông và có các đỉnh đều có bậc chẵn (ở đây là bậc 4) nên theo định lí Euler, đồ thị này có một chu trình Euler. Một chu trình Euler của đồ thị này là ABCDEADBECA.

Lại có đồ thị b) có 5 đỉnh, tổng số bậc của hai đỉnh không kề nhau luôn không nhỏ hơn 5 nên theo định lí Ore, đồ thị b) có một chu trình Hamilton.

Một chu trình Halminton của đồ thị này là ABCDEA.

+) Đồ thị Hình 2.24 c) có các đỉnh đều có bậc là 3 nên theo định lí Euler đồ thị này không có chu trình Euler.

Lại có đồ thị c) có 8 đỉnh, mặc dù đồ thị này không thỏa mãn cả 2 định lí Ore và Dirac nhưng đồ thị vẫn có một chu trình Hamilton.

Một chu trình Hamiltol của đồ thị c) là ABCDHGFEA.

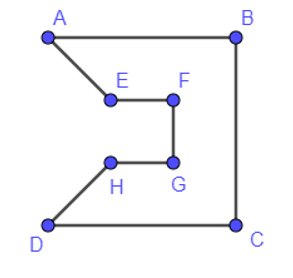
+) Đồ thị Hình 2.24 d) có đỉnh A và B là đỉnh bậc 3, nên theo định lí Euler đồ thị này không có chu trình Euler. Đồ thị d) này cũng không có chu trình Hamilton.

Bài 2.8 trang 44 Chuyên đề Toán 11: Có thể nào đi dạo chơi qua các cây cầu trong Hình 2.25, mỗi cây cầu vừa đúng một lần?

Lời giải:

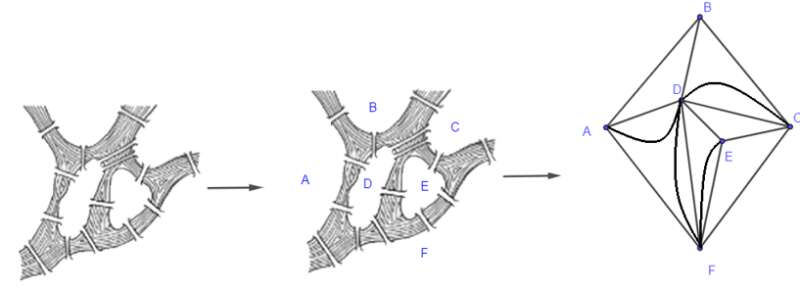
Bằng cách loaị bỏ tất cả các chi tiết ngoại trừ các vùng đất và các cây cầu, sau đó thay thế mỗi vùng đất bằng một điểm và thay thế mỗi câu cầu nối hai vùng đất bằng một đoạn nối hai điểm, ta nhận được một đồ thị G có 6 đỉnh (tương ứng 6 vùng đất) và có 15 cạnh (tương ứng 15 cây cầu) như hình vẽ trên.

Ta thấy đồ thị G liên thông và đỉnh A có bậc 4, đỉnh B có bậc 3, đỉnh C có bậc 5, đỉnh D có bậc 8, đỉnh E có bậc 4, đỉnh F có bậc 6 hay mọi đỉnh của G đều có bậc chẵn, chỉ trừ B và C có bậc lẻ, do đó theo Định lí 2, ta suy ra đồ thị G có một đường đi Euler từ A đến B. Chẳng hạn, một đường đi Euler của đồ thị G là BAFCDADFDEFECDBC.

Vậy có thể đi dạo chơi qua các cây cầu trong Hình 2.25, mỗi cây cầu vừa đúng một lần.

Bài 2.9 trang 44 Chuyên đề Toán 11: Cho đồ thị G như Hình 2.26. Tìm một chu trình Hamilton xuất phát từ đỉnh S của G.

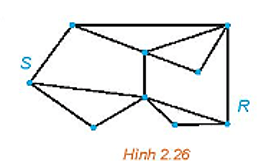
Lời giải:

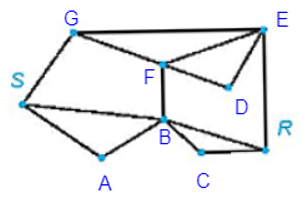
Đặt thêm tên các đỉnh vào đồ thị như hình vẽ trên.

Có thể thấy một chu trình Hamilton xuất phát từ đỉnh S của đồ thị G là SABCREDFGS.

Bài 2.10 trang 44 Chuyên đề Toán 11: Cho đồ thị G như Hình 27. Tìm một đường đi Hamilton từ S đến R.

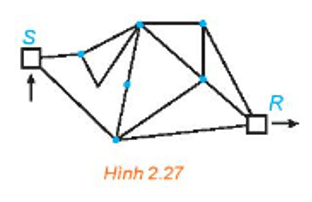
Lời giải:

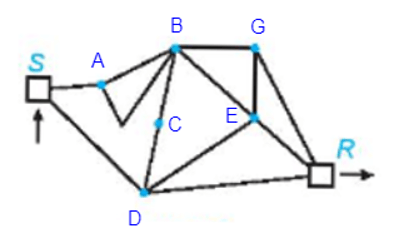
Đặt thêm tên các đỉnh vào đồ thị như hình vẽ trên.

Có thể thấy một đường đi Hamilton từ đỉnh S đến đỉnh R của đồ thị G là SABCDEGR.

Bài 2.11 trang 45 Chuyên đề Toán 11: Hãy chỉ ra một ví dụ chứng tỏ rằng điều kiện bậc của mỗi đỉnh của đồ thị G không nhỏ hơn $\frac{n}{2}$ trong Định lí Dirac, không thể thay bằng điều kiện “bậc của mỗi đỉnh không nhỏ hơn $\frac{n-1}{2}$”.

Lời giải:

Cho đơn đồ thị G có 5 đỉnh như hình vẽ sau:

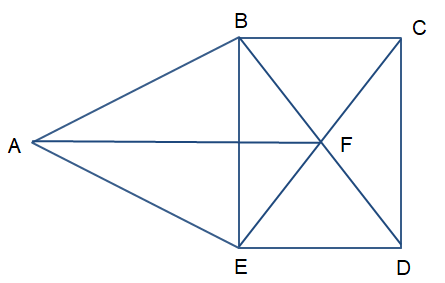
Mỗi đỉnh của đồ thị này đều có bậc là 2 hoặc 3, đều không nhỏ hơn $\frac{5-1}{2}=2$, thỏa mãn điều kiện của định lí Dirac nếu thay điều kiện “bậc của mỗi đỉnh của đồ thị G không nhỏ hơn $\frac{n}{2}$” bằng điều kiện “bậc của mỗi đỉnh không nhỏ hơn $\frac{n-1}{2}$”.

Định lí Dirac là một điều kiện đủ cho sự tồn tại chu trình Hamilton, nhưng đồ thị trên lại không có chu trình Hamilton. Do vậy, đây vì ví dụ cần đưa ra để chứng tỏ rằng điều kiện bậc của mỗi đỉnh của đồ thị G không nhỏ hơn $\frac{n}{2}$ trong Định lí Dirac, không thể thay bằng điều kiện “bậc của mỗi đỉnh không nhỏ hơn $\frac{n-1}{2}$”.

Bài 2.12 trang 45 Chuyên đề Toán 11: a) Giả sử G là một đồ thị với n đỉnh và $\frac{\left(n-1\right)\left(n-2\right)}{2}+2$ cạnh. Sử dụng Định lí Ore, hãy chứng minh G có một chu trình Hamilton.

b) Tìm một đồ thị với n đỉnh và $\frac{\left(n-1\right)\left(n-2\right)}{2}+1$ cạnh mà không có chu trình Hamilton.

Lời giải:

a) Định lí Ore: Nếu G là một đồ thị có n đỉnh (n $\ge$ 3) và mỗi cặp đỉnh không kề nhau đều có tổng bậc không nhỏ hơn n thì G có một chu trình Hamilton.

Ta có lí thuyết: Giả sử G là đồ thị đơn gồm n đỉnh và m cạnh. Nếu m $\ge \frac{n^2-3n +6}{2}$ thì G là đồ thị có chu trình Hamilton.

Áp dụng vào bài toán ta được điều phải chứng minh.

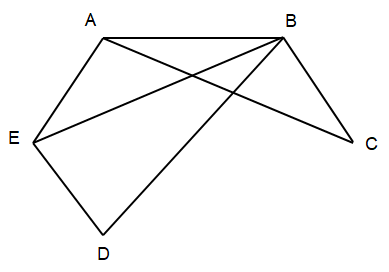
b) Ta có đồ thị sau có 5 đỉnh, 7 cạnh và đồ thị không có chu trình Hamilton.

Bài 2.13 trang 45 Chuyên đề Toán 11: Với giá trị nào của n thì đồ thị đầy đủ K_n có một chu trình Euler? Có một đường đi Euler?

Lời giải:

Đồ thị đầy đủ K_n có n ≥ 2, n ∈ ℕ.

Đồ thị đầy đủ K_n là đồ thị liên thông.

Mỗi đỉnh của K_n đều có bậc là n – 1.

+) Theo định lí Euler, K_n­ có chu trình Euler khi K_n liên thông (đã thỏa mãn) và mọi đỉnh của K_n đều có bậc chẵn, điều này có nghĩa để K_n­ có một chu trình Euler thì n – 1 phải là số chẵn hay n phải là số lẻ, tức là n = 2k + 1 (k ∈ ℕ^*). Vậy với n = 2k + 1 (k ∈ ℕ^*) thì đồ thị đầy đủ K_n có một chu trình Euler.

+) Đồ thị K_n có một đường đi Euler từ A đến B khi và chỉ khi K_n liên thông và mọi đỉnh của K_n đều có bậc chẵn, chỉ trừ A và B có bậc lẻ. Mà mọi đỉnh của K_n đều có bậc là n – 1, nghĩa là mọi đỉnh của K_n đều có bậc chẵn hoặc đều có bậc lẻ.

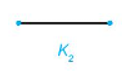
- Với n = 2, ta có K₂ có 2 đỉnh đều có bậc là 1 (là bậc lẻ) nên ta có đường đi Euler từ đỉnh này qua đỉnh còn lại.

- Với n > 2, n ∈ ℕ^* thì mọi đỉnh của K_n đều có bậc cùng chẵn hoặc cùng lẻ lớn hơn 2, do đó không thỏa mãn điều kiện để K_n có đường đi Euler.

Vậy đồ thị đầy đủ K_n­ có một đường đi Euler khi n = 2.

Bài 2.14 trang 45 Chuyên đề Toán 11: Với giá trị nào của n thì đồ thị đầy đủ K_n có một chu trình Hamilton? Có một đường đi Hamilton?

Lời giải:

Đồ thị đầy đủ K_n có n ≥ 2, n ∈ ℕ.

+ Với n = 2 ta có K₂ không có chu trình Hamilton, nhưng có đường đi Hamilton (đi từ đỉnh này qua đỉnh còn lại).

+ Với n ≥ 3, n ∈ ℕ.

Đồ thị đầy đủ K_n­ là một đơn đồ thị có n đỉnh và mỗi đỉnh có bậc là n – 1.

- Sử dụng định lí Ore, ta thấy K_n có một chu trình Hamilton khi mỗi cặp đỉnh không kề nhau đều có tổng bậc không nhỏ hơn n, tức là (n – 1) + (n – 1) ≥ n, tương đương với n ≥ 2, kết hợp với điều kiện suy ra n ≥ 3, n ∈ ℕ. (Ta cũng có thể sử dụng định lí Dirac để tìm điều kiện của n)

- Sử dụng Định lí 4 (suy ra từ định lí Dirac), ta thấy K_n có một đường đi Hamilton khi mỗi đỉnh có bậc không nhỏ hơn $\frac{n-1}{2}$, tức là n – 1 ≥ $\frac{n-1}{2}$, tương đương với n ≥ 1, kết hợp với điều kiện suy ra n ≥ 3, n ∈ ℕ.

Vậy với n ≥ 3, n ∈ ℕ thì đồ thị đầy đủ K_n có một chu trình Hamilton và với n ≥ 2, n ∈ ℕ thì đồ thị đầy đủ K_n có một đường đi Hamilton.