Với giải HĐ Khám phá 2 trang 67 Toán 10 Tập 1 Chân trời sáng tạo chi tiết trong Bài 2. Định lí cosin và định lí sin giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Cho tam giác ABC không phải là tam giác vuông có BC=a, AC=b, Ab=c
HĐ Khám phá 2 trang 67 Toán 10 Tập 1: a) Cho tam giác ABC không phải là tam giác vuông có và R là bán kính của đường trong ngoại tiếp tam giác đó. Vẽ đường kính BD.
i) Tính theo a và R.
ii) Tìm mối liên hệ giữa hai góc và . Từ đó chứng minh rằng
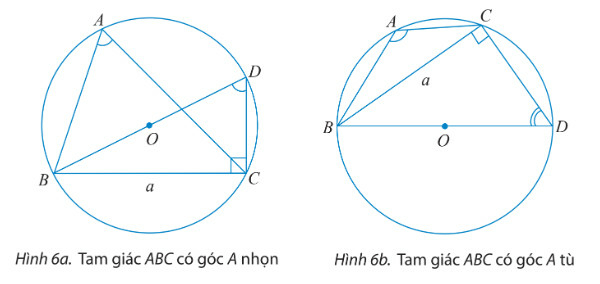
b) Cho tam giác ABC với góc A vuông. Tính sinA và so sánh a với 2R để chứng tỏ ta vẫn có công thức
Lời giải
a) Tam giác BDC vuông tại C nên
b)
TH1: Tam giác ABC có góc A nhọn
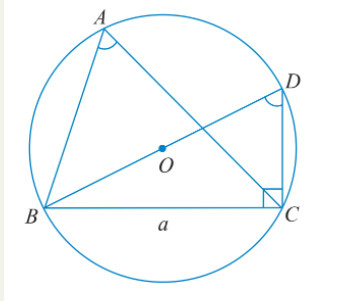
do cùng chắn cung nhỏ BC.
TH2: Tam giác ABC có góc A tù
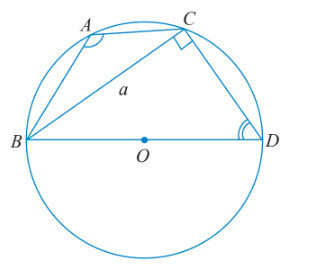
do ABDC là tứ giác nội tiếp (O).
Vậy với góc A nhọn hay tù ta đều có
b) Nếu tam giác ABC vuông tại A thì BC là đường kính của (O).
Khi đó ta có: và
Do đó ta vẫn có công thức:
Xem thêm các bài giải Toán 10 Chân trời sáng tạo hay, chi tiết khác:
HĐ Khởi động trang 65 Toán 10 Tập 1:..
HĐ Khám phá 3 trang 70 Toán 10 Tập 1: Cho tam giác ABC như Hình 10...
Bài 1 trang 72 Toán 10 Tập 1: Tính độ dài cạnh x trong các tam giác sau...
Bài 2 trang 72 Toán 10 Tập 1: Tính độ dài cạnh c trong tam giác ABC ở Hình 14...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.
