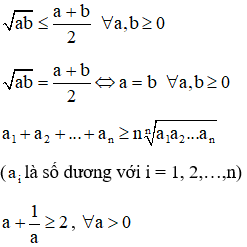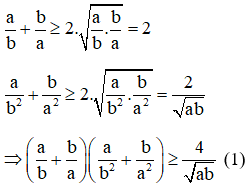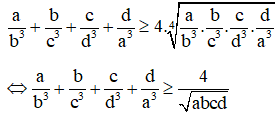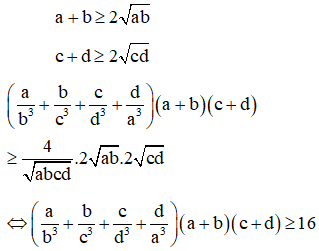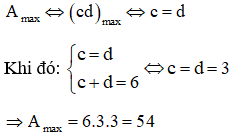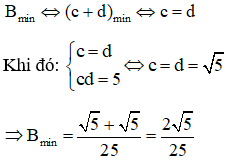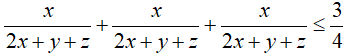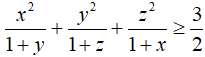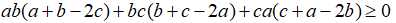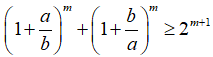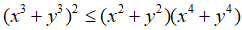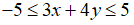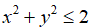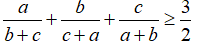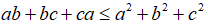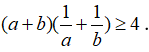Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Bất đẳng thức Cô-si (50 bài tập minh họa) HAY NHẤT 2024 gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 10 từ đó học tốt môn Toán. Mời các bạn đón xem:
Phương pháp giải Bất đẳng thức Cô-si (50 bài tập minh họa) HAY NHẤT 2024
I. Lí thuyết tổng hợp
- Định lí: Trung bình nhân của hai số không âm nhỏ hơn hoặc bằng trung bình cộng của chúng.
Đẳng thức xảy ra khi và chỉ khi a = b.
- Các hệ quả:
+ Tổng của một số dương với nghịch đảo của nó lớn hơn hoặc bằng 2.
,
+ Nếu x, y cùng dương và có tổng không đổi thì tích (xy) lớn nhất khi và chỉ khi x = y.
+ Trong tất cả các hình chữ nhật có cùng chu vi, hình vuông có diện tích lớn nhất.
+ Nếu x, y cùng dương và có tích không đổi thì tổng (x + y) nhỏ nhất khi và chỉ khi x = y.
+ Trong tất cả các hình chữ nhật có cùng diện tích, hình vuông có chu vi nhỏ nhất.
II. Các công thức
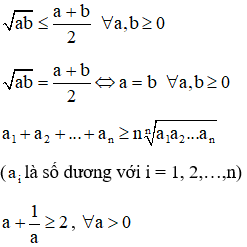
, nếu không đổi thì .
, nếu không đổi thì .
III. Ví dụ minh họa
Bài 1: Cho a, b là số dương thỏa mãn . Chứng minh rằng: .
Lời giải:
Khi a, b là số dương , , ,
Áp dụng bất đẳng thức Cô-si ta có:
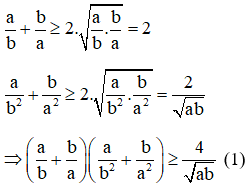
Mặt khác ta có:
(2)
Từ (1) và (2) ta có: (điều cần phải chứng minh)
Đẳng thức xảy ra khi và chỉ khi a = b = 1.
Bài 2: Cho a, b, c, d là số dương. Chứng minh rằng: .
Lời giải:
Vì a, b, c, d là số dương nên ta có: , , ,
Áp dụng Bất đẳng thức Cô-si cho bốn số dương ta có:
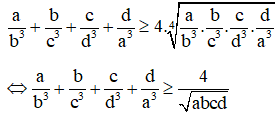
Lại có, do a, b, c, d dương nên:
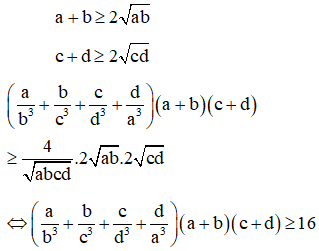
(điều cần phải chứng minh).
Bài 3: Cho hai số dương c, d. Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của các biểu thức trong các trường hợp sau:
a) c + d = 6 luôn không đổi, tìm giá trị lớn nhất của biểu thức A = (c + d).cd ;
b) c.d = 5 luôn không đổi, tìm giá trị nhỏ nhất của biểu thức .
Lời giải:
a)
Ta có: A = (c + d).cd = 6cd vì (c + d) = 6 luôn không đổi.
Áp dụng hệ quả của bất đẳng thức Cô-si ta có:
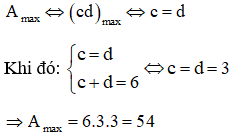
Vậy giá trị lớn nhất của A là 54 khi c = d = 3.
b)
Ta có: vì c.d = 5 luôn không đổi.
Áp dụng hệ quả của bất đẳng thức Cô-si ta có:
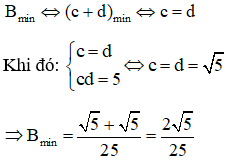
Vậy giá trị nhỏ nhất của B là khi c = d = .
IV. Bài tập tự luyện
Bài 1: Cho a, b, c là số dương thỏa mãn . Chứng minh rằng: .
Bài 2: Cho a, b, c là số dương. Chứng minh rằng .
Bài 3: Cho 3 số dương x, y, z tùy ý. Chứng minh rằng: 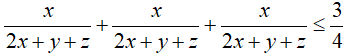
Bài 4: Cho 3 số dương x, y, z thỏa mãn: xyz=1. Chứng minh rằng: 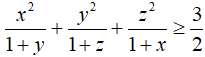
Bài 5: Cho a, b, c là độ dài ba cạnh của tam giác. Chứng minh rằng:
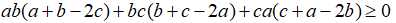
Bài 6: Cho 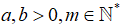 . Chứng minh rằng:
. Chứng minh rằng: 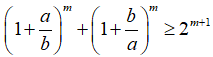
Bài 7: Chứng minh rằng với mọi số thực x, y luôn có: 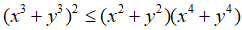
Bài 8: Hai số x, y thỏa mãn 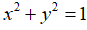 . Chứng minh rằng
. Chứng minh rằng 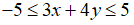
Bài 9: Cho các số không âm a, y thỏa mãn 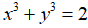 . Chứng minh rằng:
. Chứng minh rằng: 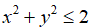
Bài 10: Cho ba số dương a, b, c. Chứng minh rằng: 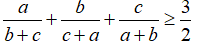
Bài 11: Chứng minh rằng với a, b, c tùy ý ta luôn có: 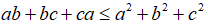
Bài 12: Cho a,b>0. Chứng minh rằng: 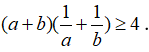
Bài 13: Cho hai số thực không âm a, b. Chứng minh (a + b)(1 + ab) ≥ 4ab.
Bài 14: Cho a, b > 0. Chứng minh: 
Xem các Phương pháp giải bài tập hay, chi tiết khác:
Bất đẳng thức chứa dấu giá trị tuyệt đối chi tiết nhất
Dấu của nhị thức bậc nhất chi tiết nhất
Công thức giải bất phương trình một ẩn chi tiết nhất
Công thức giải bất phương trình chứa dấu giá trị tuyệt đối chi tiết nhất
Dấu của tam thức bậc hai chi tiết nhất
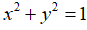
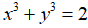
![]()