Toptailieu.vn biên soạn và giới thiệu Công thức tìm số hạng trong khai triển nhị thức Niu-tơn (50 bài tập minh họa) HAY NHẤT 2024 gồm đầy đủ các phần: Lý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh làm tốt bài tập Toán 11 từ đó học tốt môn Toán. Mời các bạn đón xem:

Công thức tìm số hạng trong khai triển nhị thức Niu-tơn (50 bài tập minh họa) HAY NHẤT 2024

1. Tổng hợp lý thuyết

Xét khai triển: (với a,b là các hệ số; x, y là biến)

- Số hạng thứ k + 1 của khai triển: 

- Hệ số của số hạng thứ k + 1 của khai triển: 

2. Các công thức

* Với khai triển (ax^p + bx^q)ⁿ (p, q là các hằng số)

Ta có: 

Số hạng chứa x^m ứng với giá trị k thỏa mãn: np – pk + qk = m

Từ đó tìm 

Vậy số hạng chứa x^m là:  với giá trị k đã tìm được ở trên.

* Với khai triển P(x) = (a + bx^p + cx^q)ⁿ  (p, q là các hằng số)

Ta có: 

Từ số hạng tổng quát của hai khai triển trên ta tính được số hạng chứa x^m.

3. Ví dụ minh họa

Ví dụ 1: Tìm số hạng thứ 6 trong khai triển: (2 – 3x)²⁰

Lời giải

Khai triển: 

Số hạng thứ k + 1 của khai triển là: 

Cần tìm số hạng thứ 6 nên k = 5.

Vậy số hạng thứ 6 trong khai triển là: .

Ví dụ 2: Tìm số hạng chứa x⁸ trong khai triển: 

Lời giải

Cần tìm số hạng chứa x⁸ nên 

Vậy số hạng chứa x⁸ trong khai triển là .

4. Bài tập vận dụng

Câu 1: Nếu bốn số hạng đầu của một hàng trong tam giác Pascal được ghi lại là:

1    16    120    560

A. 1    32    360    1680

B. 1    18    123    564

C. 1    17    137    697

D. 1    17    136    680

Khi đó 4 số hạng đầu của hàng kế tiếp là:

Hướng dẫn giải :

Đáp án : D

4 số hạng tiếp theo của tam giác Pascal là:

1    1+16=17    16+120=126    120+560=680

Câu 2: Tổng của số hạng thứ 4 trong khai triển (5a-1)⁵ và số hạng thứ 5 trong khai triển (2a- 3)⁶ là:

A.4160a²    B.-4160a²    C.4610a²    D.4620a²

Hướng dẫn giải :

Đáp án : C

Câu 3: Hệ số của số hạng chứa x4 trong khai triển P(x)=(3x² + x + 1)¹⁰ là :

A.1695    B.1485    C.405    D.360

Hướng dẫn giải :

Đáp án : A

Câu 4: Tìm số hạng chứa x¹³ trong khai triển thành các đa thức của (x + x² + x³ )¹⁰ là :

A.180    B.210    C.210x¹³    D. 180x³

Hướng dẫn giải :

Đáp án : C

+ Với 0≤q≤p≤10 thì số hạng tổng quát của khai triển (x+x²+x³)¹⁰ là:

Câu 5: Tìm hệ số chứa x¹⁰ trong khai triển (1+ x+ x² + x³)⁵

A.98    B.84    C.101    D.121

Hướng dẫn giải :

Đáp án : C

Theo khai triển nhị thức Niu-tơn, ta có:

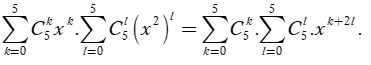
5. Bài tập tự luyện 

Câu 1: Số hạng không chứa x trong khai triển là

Lời giải:

Đáp án : B

Ta có số hạng thứ k+ 1 là :

Số hạng không chứa x tương ứng với: (60-5k)/6=0

⇔ 60 – 5k= 0 ⇔ k= 12.

Do vậy số hạng cần tìm là: 

Câu 2: Trong khai triển ( x - y)¹¹, hệ số của số hạng chứa x⁸y³ là:

Lời giải:

Đáp án : A

Câu 3: Trong khai triển nhị thức (2+ x)6 xét các khẳng định sau:

I. Gồm có 7 số hạng.

II. Số hạng thứ 3 là 16x.

III. Hệ số của x5 là 12.

Trong các khẳng định trên

A. Chỉ I và III đúng

B. Chỉ II và III đúng

C. Chỉ I và II đúng

D. Cả ba đúng

Lời giải:

Đáp án : A

Câu 4: Có bao nhiêu số hạng hữu tỉ trong khai triển .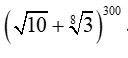

A.37    B.38    C.36    D.39

Lời giải:

Đáp án : B

⇒ k= 8t ( với t nguyên)

Lại có: 0≤k≤300 nên 0≤8t≤300

⇔ 0≤t≤37,5. Mà t nguyên nên t ∈ {0,1,2,3..., 37}.

Có 38 giá trị nguyên của t thỏa mãn. Suy ra có 38 giá trị của k thỏa mãn.

⇒ Có 38 số hạng hữu tỉ trong khai triển đã cho.

Câu 5: Tìm hệ số của x⁵ trong khai triển P(x) = ( x+1)⁶ +(x+ 1)⁷ + ( x+ 1)⁸ + ..+ (x+ 1)¹² .

A.1711    B.1287    C.1716    D.1715

Lời giải:

Đáp án : D

Câu 6: Tìm hệ số chứa x¹² trong khai triển ( 3x+ x²)¹⁰

A.145654    B.298645    C.295245    D.Đáp án khác

Lời giải:

Đáp án :

Theo khai triển nhị thức Niu-tơn, ta có số hạng thứ k+ 1 trong khai triển là:

Câu 7: Khai triển đa thức P(x) = (5x - 1)²⁰⁰³ ta được :

P(x)= a₂₀₀₃.x²⁰⁰³ + a₂₀₀₂.x²⁰⁰² + ...+ a₁x+ a₀.

Mệnh đề nào sau đây đúng?

Lời giải:

Đáp án : C

Câu 8: Tìm hệ số chứa x⁴ trong khai triển (2x+ 1/2x)¹⁰

A.1960    B.1920    C.1864    D.1680

Lời giải:

Đáp án : B

Câu 9: Tìm số hạng không chứa x trong khai triển: ( xy²- 1/xy)⁸

A.70y⁴ B.25y⁴ C.50y⁵ D.80y⁴

Lời giải:

Đáp án :

Theo khai triển nhị thức Niu-tơn, ta có:

Số hạng không chứa x ứng với: 8 - 2k=0 ⇔ k= 4

⇒ số hạng cần tìm 

Câu 10: Tìm số hạng đứng vị trí chính giữa trong khai triển: ( x²+ xy)²⁰

Lời giải:

Đáp án : D

Theo khai triển nhị thức Niu-tơn, ta có:

Câu 11: Khai triển đa thức: P(x)= ( 2 x- 1)¹⁰⁰⁰ ta được:

P(x)= a₁₀₀₀x¹⁰⁰⁰ + a₉₉₉x⁹⁹⁹+ ....+ a₁x+ a₀ .Tính a₁₀₀₀ + a₉₉₉ + ...+ a₁ + a₀ ?

A.-1    B.0    C.2    D.1

Lời giải:

Đáp án : D

Ta có: (x) = a₁₀₀₀x¹⁰⁰⁰ + a₉₉₉x⁹⁹⁹+ ....+ a₁x+ a₀

Cho x = 1 ta được P(1) = a₁₀₀₀ + a₉₉₉ + a₉₉₈ + ...+ a₁+ a₀ (1)

Mặt khác: P(x) = ( 2x-1)¹⁰⁰⁰ nên P(1)= (2.1 – 1)¹⁰⁰⁰ = 1 (2)

Từ (1) và (2) suy ra: a₁₀₀₀ + a₉₉₉ + a₉₉₈ + ...+ a₁+ a₀ = 1

Câu 12: Tìm hệ số của x⁵ trong khai triển P(x) = x.(2+ x)⁵ + x²( 1 + x )¹⁰

A.110    B.120    C.130    D.140

Lời giải:

Đáp án : C

Câu 13: Số hạng không chứa x trong khai triển (x² + 1/x - 1)¹⁰ là

A.1951    B.1950    C.3150    D.-360

Lời giải:

Đáp án : A

Câu 14: Số hạng chứa x⁸ trong khai triển (x³ - x² -1)⁸ là

A.168x⁸    B.168    C.238x⁸    D.238

Lời giải:

Đáp án : D

Câu 15: Tìm hệ số của x⁵ trong khai triển P(x)= (1+ x)+ 2(1+x)² + ...+ 8(1+x)⁸

A.487    B.636    C.742    D.568

Lời giải:

Đáp án : B

Các biểu thức ( 1 + x ) ; 2( 1 + x )² ; 3(1+x)³ ; 4(1+ x)⁴ không chứa số hạng chứa x⁵

Hệ số của số hạng chứa x5 trong khai triển 5(1+x)⁵ là 

Hệ số của số hạng chứa x5 trong khai triển 6(1+x)⁶ là 

Hệ số của số hạng chứa x5 trong khai triển 7(1+x)⁷ là 

Hệ số của số hạng chứa x5 trong khai triển 8(1+ x)⁸ là 

Vậy hệ số của x₅ trong khai triển P(x) là :

Xem thêm các Phương pháp giải hay, chi tiết khác: 

Công thức tính xác suất

Phương pháp quy nạp toán học và cách giải

Dãy số và cách giải các dạng bài tập

Cấp số cộng và cách giải các dạng bài tập

Cấp số nhân và cách giải các dạng bài tập