Toptailieu.vn biên soạn và giới thiệu Lý thuyết Tổng các góc trong một tam giác (Kết nối tri thức) Toán 7 hay, ngắn gọn và bài tập tự luyện có lời giải chi tiết sẽ giúp học sinh nắm vững nội dung kiến thức từ đó dễ dàng làm các bài tập Toán 7.
Lý thuyết Tổng các góc trong một tam giác (Kết nối tri thức) Toán 7
Lý thuyết
• Tổng ba góc trong một tam giác là tổng số đo ba góc trong tam giác đó.
• Tổng ba góc trong một tam giác bằng 180°.
• Góc ngoài của tam giác là góc kề bù với 1 góc của tam giác.
• Mỗi góc ngoài của một tam giác có số đo bằng tổng số đo hai góc trong không kề với nó.
Ví dụ:
+ Cho tam giác ABC, ta có các góc A2; góc B; góc C là các góc trong của tam giác.
Qua A kẻ đường thẳng . Khi đó ta có:
(hai góc so le trong)
(hai góc so le trong)
Mà
Nên:
Do đó tổng ba góc trong tam giác ABC bằng 180°.
+ Trong hình dưới đây, ta thấy góc ACD kề bù với góc ACB (góc trong tam giác ABC). Do đó góc ACD gọi là góc ngoài của tam giác ABC.
Khi đó ta có: .
Chú ý:
• Tam giác có ba góc đều nhọn được gọi là tam giác nhọn.
Ví dụ: Tam giác ABC có ; ; . Như vậy các góc A; góc B; góc C đều là góc nhọn. Do đó tam giác ABC gọi là tam giác nhọn.
• Tam giác có một góc tù được gọi là tam giác tù.
Ví dụ: Tam giác ABC trong hình dưới đây có là góc tù nên tam giác ABC gọi là tam giác tù.
• Tam giác có một góc vuông được gọi là tam giác vuông. Trong tam giác vuông, hai cạnh của góc vuông được gọi là cạnh góc vuông; cạnh còn lại được gọi là cạnh huyền.
• Hai góc có tổng số đo bằng 90° được gọi là hai góc phụ nhau. Trong tam giác vuông hai góc nhọn phụ nhau.
Ví dụ: Tam giác DGH có nên tam giác DGH gọi là tam giác vuông. Cạnh DG và DH gọi là cạnh góc vuông; cạnh GH là cạnh huyền. Góc G và góc H là hai góc phụ nhau.
Bài 1. Tính số đo x trong các hình dưới đây:
Hướng dẫn giải
a) Tam giác ABC có: (tổng ba góc trong tam giác)
Do đó:
Vậy
b) Tam giác DGE có: (tổng ba góc trong tam giác)
Do đó:
Vậy
c) Tam giác IJK có: (tổng ba góc trong tam giác)
Do đó:
Vậy
Bài 2. Tính số đo a; b; c trong các hình dưới đây:
Hướng dẫn giải
Ta có: (góc ngoài của tam giác)
Do đó:
Ta có: (hai góc đối đỉnh)
Do đó:
Có: (tổng ba góc trong tam giác)
Do đó:
Có: (hai góc kề bù)
Do đó:
Vậy ; ; .
Bài 3. Trong các tam giác dưới đây. Tam giác nào là tam giác nhọn, tam giác vuông, tam giác tù?
Hướng dẫn giải
a) Tam giác MLN có: (tổng ba góc trong tam giác)
Do đó: ⟹
Như vậy góc L là góc vuông nên tam giác MLN là tam giác vuông.
b) Tam giác POQ có: (tổng ba góc trong tam giác)
Do đó: ⟹< 90°
Như vậy góc Q; góc O; góc P là góc nhọn nên tam giác POQ là tam giác nhọn.
c) Tam giác SRT có: (tổng ba góc trong tam giác)
Do đó: ⟹> 90°
Như vậy góc R là góc tù nên tam giác SRT là tam giác tù.
B. Trắc nghiệm Tổng các góc trong một tam giác (Kết nối tri thức 2023) có đáp án
I. Nhận biết
Câu 1. Tổng ba góc trong một tam giác bất kì luôn bằng:
A. 90°;
B. 180°;
C. 270°;
D. 360°.
Hướng dẫn giải
Đáp án: B
Giải thích:
Vì tổng ba góc trong một tam giác luôn bằng 180°.
Nên ta chọn phương án B.
Câu 2. Tam giác nhọn là tam giác:
A. Có cả ba góc đều nhỏ hơn 90°;
B. Có một góc bất kì bằng 90°;
C. Có một góc bất kì lớn hơn 90°;
D. Cả ba góc đều nhỏ hơn 180°.
Hướng dẫn giải
Đáp án: A
Giải thích:
Tam giác có ba góc đều nhọn (tức là ba góc đều nhỏ hơn 90°) được gọi là tam giác nhọn.
Vậy ta chọn phương án A.
Câu 3. Cho ∆ABC vuông tại B. Kết luận nào sau đây sai?
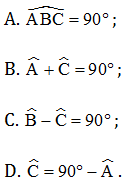
Hướng dẫn giải
Đáp án: C
Giải thích:
⦁ Vì ∆ABC vuông tại B nên ta có .
Do đó phương án A đúng.
⦁ Ta có ∆ABC vuông tại B.
Suy ra .
Do đó .
Vì vậy phương án B, D đúng.
Suy ra phương án C sai.
Vậy ta chọn phương án C.
Câu 4. Hai góc phụ nhau là:
A. Hai góc có số đo không nhỏ hơn 90°;
B. Hai có tổng số đo bằng 180°;
C. Hai góc có giá trị tuyệt đối của hiệu số đo bằng 90°;
D. Hai góc có tổng số đo bằng 90°.
Hướng dẫn giải
Đáp án: D
Giải thích:
Hai góc có tổng số đo bằng 90° được gọi là hai góc phụ nhau.
Hai góc có tổng số đo bằng 180° được gọi là hai góc bù nhau.
Vậy ta chọn phương án D.
Câu 5. Tam giác có một góc lớn hơn 90° là:
A. Tam giác nhọn;
B. Tam giác tù;
C. Tam giác vuông;
D. Đáp án khác.
Hướng dẫn giải
Đáp án: B
Giải thích:
Tam giác có một góc tù (tức là góc đó lớn hơn 90°) thì được gọi là tam giác tù.
Vậy ta chọn phương án B.
II. Thông hiểu
Câu 1. ∆ABC có , . Khi đó có số đo bằng:
A. 90°;
B. 60°;
C. 45°;
D. 75°.
Hướng dẫn giải
Đáp án: B
Giải thích:
∆ABC có: (định lí tổng ba góc trong một tam giác)
Suy ra .
Vậy ta chọn phương án B.
Câu 2. Cho ∆MNP có , biết . Khi đó số đo của bằng:
A. 75°;
B. 45°;
C. 70°;
D. 60°.
Hướng dẫn giải
Đáp án: C
Giải thích:
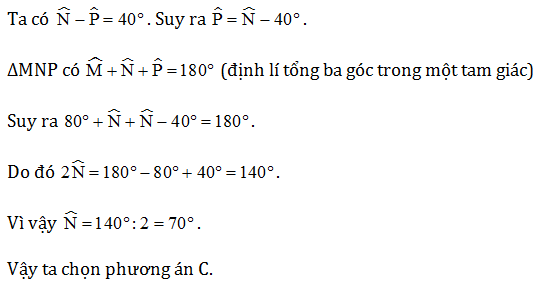
Câu 3. Cho ∆ABC có và . Số đo của bằng:
A. 70°;
B. 35°;
C. 40°;
D. 50°.
Hướng dẫn giải
Đáp án: B
Giải thích:
∆ABC có: (định lí tổng ba góc trong một tam giác)
Suy ra .
Do đó .
Vì vậy .
Vậy ta chọn phương án B.
Câu 4. Cho hình vẽ bên.
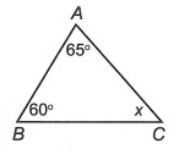
Số đo của x bằng:
A. 60°;
B. 30°;
C. 45°;
D. 55°.
Hướng dẫn giải
Đáp án: D
Giải thích:
∆ABC có: (định lí tổng ba góc trong một tam giác)
Suy ra 65° + 60° + x = 180°
Do đó x = 180° – 65° – 60° = 55°.
Vậy ta chọn phương án D.
Câu 5. Cho hình vẽ bên.
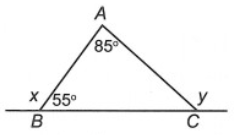
Số đo của x và y là:
A. x = 140° và y = 125°;
B. x = 55° và y = 40°;
C. x = 125° và y = 140°;
D. x = 40° và y = 55°.
Hướng dẫn giải
Đáp án: C
Giải thích:
⦁ Ta có y được gọi là góc ngoài tại đỉnh C của ∆ABC.
Suy ra .
⦁ Lại có: (hai góc kề bù)
Suy ra .
Vậy x = 125° và y = 140°.
Do đó ta chọn phương án C.
Câu 6. Cho ∆ABC có , . Khi đó ∆ABC là:
A. Tam giác tù;
B. Tam giác nhọn;
C. Tam giác vuông;
D. Đáp án khác.
Hướng dẫn giải
Đáp án: A
Giải thích:
∆ABC có: (định lí tổng ba góc trong một tam giác)
Suy ra .
Vì vậy là góc tù.
Do đó ∆ABC là tam giác tù.
Vậy ta chọn phương án A.
Câu 7. Kết luận nào sau đây đúng?
A. Một tam giác chỉ có tối đa hai góc nhọn;
B. Một tam giác chỉ có nhiều nhất một góc tù;
C. Trong một tam giác, có ít nhất hai góc có số đo nhỏ hơn 60°;
D. Trong một tam giác, số đo của mỗi góc luôn nhỏ hơn tổng số đo các góc còn lại.
Hướng dẫn giải
III. Vận dụng
Câu 1. Cho ∆MNP. Các đường phân giác trong các , cắt nhau tại I. Kết luận nào sau đây đúng?
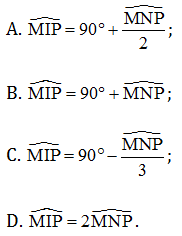
Hướng dẫn giải
Đáp án: A
Giải thích:
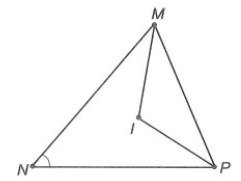
Ta có:
⦁ (do MI là phân giác của );
⦁ (do PI là phân giác của ).
∆MIP có: (định lí tổng ba góc trong một tam giác)
Suy ra
(1)
∆MNP có: (định lí tổng ba góc trong một tam giác)
Suy ra (2)
Thế (2) vào (1) ta được: .
Vậy ta chọn phương án A.
Câu 2. Cho ∆ABC có , . Gọi AD là tia nằm giữa hai tia AB và AC sao cho . Số đo của bằng:
A. 10°;
B. 30°;
C. 45°;
D. 60°.
Hướng dẫn giải
Đáp án: D
Giải thích:
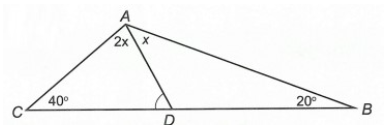

Vậy đáp án đúng là D
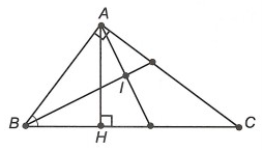
Câu 3. Cho ∆ABC vuông tại A. Kẻ AH vuông góc với BC (H ∈ BC). Các tia phân giác của và cắt nhau tại I. Khi đó ∆AIB là:
A. Tam giác vuông tại I;
B. Tam giác vuông tại B;
C. Tam giác nhọn;
D. Tam giác tù.
Hướng dẫn giải
Đáp án: A
Giải thích:

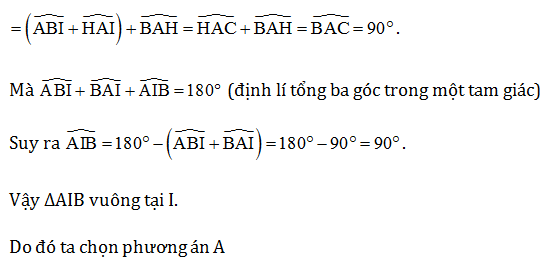
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.