Lý thuyết Trường hợp bằng nhau thứ hai và thứ ba của tam giác (Kết nối tri thức) Toán 7

Giang Ngày: 24-07-2023 Lớp 7

381

Toptailieu.vn biên soạn và giới thiệu Lý thuyết Trường hợp bằng nhau thứ hai và thứ ba của tam giác (Kết nối tri thức) Toán 7 hay, ngắn gọn và bài tập tự luyện có lời giải chi tiết sẽ giúp học sinh nắm vững nội dung kiến thức từ đó dễ dàng làm các bài tập Toán 7.

Lý thuyết Trường hợp bằng nhau thứ hai và thứ ba của tam giác (Kết nối tri thức) Toán 7

Lý thuyết

1. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh (c.g.c)

• Trong tam giác ABC, góc BAC (hay góc A) được gọi là góc xen giữa của hai cạnh AB và AC.

Lý thuyết Toán 7 Kết nối tri thức Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác (ảnh 1)

• Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.

Ví dụ:

+ Tam giác ABC và tam giác EFD có cạnh AB = EF = 5cm; AC = ED = 3cm; góc A là góc xen giữa của cạnh AB và AC, góc E là góc xen giữa của cạnh EF và ED; $\hat{A} = \hat{E} = 79 °$ .

Lý thuyết Toán 7 Kết nối tri thức Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác (ảnh 2)

Khi đó ta có $Δ A B C = Δ E F D$ theo trường hợp cạnh góc cạnh (c.g.c)

2. Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc (g.c.g)

• Trong tam giác ABC, hai góc ABC, ACB (hay góc B và góc C) được gọi là hai góc kề cạnh BC của tam giác ABC.

Lý thuyết Toán 7 Kết nối tri thức Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác (ảnh 3)

• Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.

Ví dụ

+ Tam giác ABC và tam giác EFD có $\hat{B} = \hat{F} = 37 °$ ; $\hat{C} = \hat{D} = 64 °$ ; góc B và góc C là hai góc kề của cạnh BC, góc F và góc D là hai góc kề của cạnh FD; cạnh BC = FD = 6cm.

Khi đóta có < $Δ A B C = Δ E F D$ theo trường hợp góc cạnh góc (g.c.g)

Bài tập Trường hợp bằng nhau thứ hai và thứ ba của tam giác

Bài 1. Trong mỗi hình dưới đây, hãy chỉ ra một cặp tam giác bằng nhau và giải thích vì sao chúng bằng nhau.

Lý thuyết Toán 7 Kết nối tri thức Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác (ảnh 5)

Hướng dẫn giải

a) Hai tam giác AED và CEB có:

AE = CE

$\hat{A E D} = \hat{C E B}$ (hai góc đối đỉnh)

DE = BE

Do đó $Δ A E D = Δ C E B$ (c.g.c)

b) Hai tam giác QGH và QIH có:

$\hat{G Q H} = \hat{I Q H}$

QH là cạnh chung

$\hat{G H Q} = \hat{I H Q}$

Do đó $Δ Q G H = Δ Q I H$ (g.c.g)

Bài 2. Cho hình vẽ dưới đây, biết CE = DE và $\hat{C E A} = \hat{D E A}$ .

Lý thuyết Toán 7 Kết nối tri thức Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác (ảnh 6)

Chứng minh rằng:

a) $Δ A E C = Δ A E D$ ;

b) $Δ A B C = Δ A B D$ .

Hướng dẫn giải

a) Xét $Δ A E C$ và $Δ A E D$ có:

CE = DE (theo giả thiết)

$\hat{C E A} = \hat{D E A}$ (theo giả thiết)

AE là cạnh chung

Do đó $Δ A E C = Δ A E D$ (c.g.c)

b) Vì $Δ A E C = Δ A E D$ (theo câu a)

⇒ AC = AD (2 cạnh tương ứng) và $\hat{C A E} = \hat{D A E}$ (2 góc tương ứng)

Xét $Δ A B C$ và $Δ A B D$ có:

AC = AD (chứng minh trên)

$\hat{C A E} = \hat{D A E}$ (chứng minh trên)

AB là cạnh chung

Do đó $Δ A B C = Δ A B D$ (c.g.c)

Bài 3. Cho hình vẽ dưới đây, biết đoạn thẳng JK song song và bằng đoạn thẳng ML.

Chứng minh rằng:

a) $Δ J O K = Δ L O M$

b) OP = OQ.

Hướng dẫn giải

a) Vì JK ∥ML nên:

$\hat{OJ K} = \hat{O L M}$ (2 góc so le trong)

$\hat{O K J} = \hat{O M L}$ (2 góc so le trong)

Xét $Δ JO K$ và $Δ L O M$ có:

$\hat{OJ K} = \hat{O L M}$ (chứng minh trên)

JK = ML (theo giả thiết)

$\hat{O K J} = \hat{O M L}$ (chứng minh trên)

Do đó $Δ J O K = Δ L O M$ (g.c.g)

b) Vì $Δ J O K = Δ L O M$ (theo câu a)

⇒ KO = MO (2 cạnh tương ứng)

Xét $Δ K O P$ và $Δ M O Q$ có:

$\hat{O K J} = \hat{O M L}$ (chứng minh trên)

KO = MO (chứng minh trên)

$\hat{K O P} = \hat{M O Q}$ (2 góc đối đỉnh)

Do đó $Δ K O P = Δ M O Q$ (g.c.g)

⇒ OP = OQ (2 cạnh tương ứng).

B. Trắc nghiệm Trường hợp bằng nhau thứ hai và thứ ba của tam giác (Kết nối tri thức 2023) có đáp án

I. Nhận biết

Câu 1. Cho ∆ABC và ∆MNP có AB = NM, AC = NP và $\hat{A} = \hat{N}$ . Trong các khẳng định sau, khẳng định nào sai?

A. ∆ABC = ∆NMP;

B. ∆BAC = ∆MNP;

C. ∆ABC = ∆MNP;

D. ∆CAB = ∆PNM.

Hướng dẫn giải

Đáp án: C

Giải thích:

Xét ∆ABC và ∆NMP, có:

AB = NM (giả thiết)

AC = NP (giả thiết)

$\hat{A} = \hat{N}$ (giả thiết)

Do đó ∆ABC = ∆NMP (c.g.c)

Ta cũng có thể kí hiệu là: ∆BAC = ∆MNP hay ∆CAB = ∆PNM.

Do đó kí hiệu ở các phương án A, B, D đúng, kí hiệu ở phương án C sai.

Vậy ta chọn phương án C.

Câu 2. Điền từ còn thiếu vào chỗ chấm để được phát biểu đúng:

Nếu hai ... và góc xen giữa của tam giác này bằng hai cạnh và ... xen giữa của tam giác kia thì hai tam giác đó bằng nhau.

A. cạnh và góc;

B. góc và góc;

C. cạnh và cạnh;

D. góc và cạnh.

Hướng dẫn giải

Đáp án: A

Giải thích:

Ta có phát biểu sau:

Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.

Suy ra từ cần điền là cạnh và góc.

Vậy chọn đáp án A.

Câu 3. Cặp tam giác nào sau đây bằng nhau?

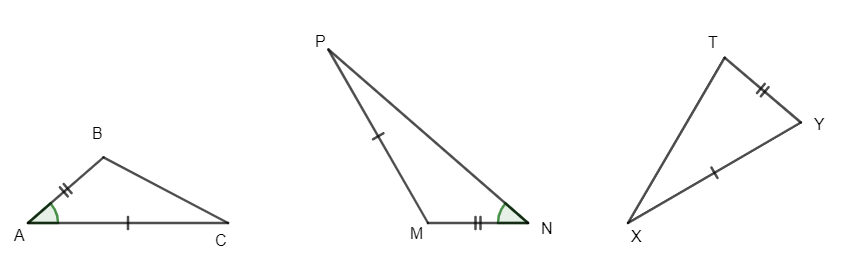
TOP 20 câu Trắc Nghiệm Trường hợp bằng nhau thứ hai và thứ ba của tam giác - Toán 7 Kết nối tri thức (ảnh 1)

Khẳng định nào sau đây đúng?

A. ∆ABC = ∆MNP;

B. ∆ABC = ∆XYT;

C. ∆MNP = ∆XYT;

D. Không có cặp tam giác nào bằng nhau.

Hướng dẫn giải

Đáp án: B

Giải thích:

⦁ Xét ∆ABC và ∆MNP, có:

AB = MN (giả thiết)

AC = MP (giả thiết)

$\hat{B A C} = \hat{M N P}$ (giả thiết)

Tuy nhiên hai góc $\hat{B A C}$ và $\hat{M N P}$ không xen giữa hai cạnh đã cho.

Suy ra ∆ABC và ∆MNP không bằng nhau. Do đó A sai.

⦁ Xét ∆MNP và ∆XYT, có:

MN = YT (giả thiết)

MP = XY (giả thiết)

Chưa đủ điều kiện để suy ra ∆MNP và ∆XYT bằng nhau. Do đó B sai.

⦁ Xét ∆ABC và ∆XYT, có:

AB = YT (giả thiết)

AC = XY (giả thiết)

Chưa đủ điều kiện để suy ra ∆ABC và ∆XYT bằng nhau. Do đó C sai.

Vì vậy không có cặp tam giác nào bằng nhau.

Vậy chọn đáp án D

Câu 4. Cho ∆ABC = ∆MNP (c – g – c). Đỉnh A và B của tam giác ABC tương ứng với đỉnh nào của tam giác MNP?

A. N và P;

B. M và N;

C. M và P;

D. N và M.

Hướng dẫn giải

Đáp án: B

Giải thích:

Vì ∆ABC = ∆MNP (c – g – c) nên đỉnh A tương ứng với M, B tương ứng với N, C tương ứng với P.

Vậy ta chọn phương án B.

Câu 5. Cho hình vẽ bên.

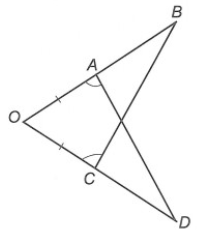
TOP 20 câu Trắc Nghiệm Trường hợp bằng nhau thứ hai và thứ ba của tam giác - Toán 7 Kết nối tri thức (ảnh 1)

Cặp tam giác nào sau đây bằng nhau?

A. ∆OAC và ∆OBD;

B. ∆OAD và ∆OCB;

C. ∆ABC và ∆BCD;

D. ∆ACD và ∆ABD.

Hướng dẫn giải

Đáp án: B

Giải thích:

⦁ Xét ∆OAD và ∆OCB, có:

$\hat{O A D} = \hat{O C B}$ (giả thiết)

OA = OC (giả thiết)

$\hat{A O C}$ là góc chung.

Do đó ∆OAD = ∆OCB (g.c.g)

Vì vậy phương án B đúng.

⦁ Phương án A sai vì OA < OB và A ∈ OB.

⦁ Phương án C, D sai vì không có các cặp cạnh, cặp góc tương ứng thỏa mãn cả ba trường hợp bằng nhau của hai tam giác.

Vậy ta chọn phương án B.

II. Thông hiểu

Câu 1. Cho hình vẽ bên.

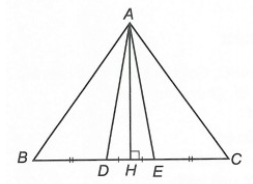
TOP 20 câu Trắc Nghiệm Trường hợp bằng nhau thứ hai và thứ ba của tam giác - Toán 7 Kết nối tri thức (ảnh 1)

Có bao nhiêu cặp tam giác bằng nhau?

A. 1;

B. 2;

C. 3;

D. 4.

Hướng dẫn giải

Đáp án: D

Giải thích:

⦁ Xét ∆AHD và ∆AHE, có:

AH là cạnh chung.

$\hat{A H D} = \hat{A H E} = 90 °$ .

HD = HE (giả thiết)

Do đó ∆AHD = ∆AHE (c.g.c)

⦁ Ta có HD = HE (giả thiết) và DB = EC (giả thiết)

Suy ra HD + DB = HE + EC.

Khi đó HB = HC.

Xét ∆AHB và ∆AHC, có:

AH là cạnh chung.

$\hat{A H B} = \hat{A H C} = 90 °$ .

HB = HC (chứng minh trên)

Do đó ∆AHB = ∆AHC (c.g.c)

⦁ Xét ∆ADB và ∆AEC, có:

AD = AE (do ∆AHD = ∆AHE)

DB = EC (giả thiết)

AB = AC (∆AHB = ∆AHC)

Do đó ∆ADB = ∆AEC (c.c.c)

⦁ Ta có: BE = BD + DE, DE = DE + EC

Mà BD = EC (gt) nên BE = DE

Xét ∆AEB và ∆ADC, có:

AD = AE (do ∆AHD = ∆AHE)

BE = DC (giả thiết)

AB = AC (∆AHB = ∆AHC)

Do đó ∆AEB = ∆ADC (c.c.c)

Vậy có 4 cặp tam giác bằng nhau.

Câu 2. Cho ∆ABC. Gọi I là trung điểm của AC. Trên tia đối của tia IB, lấy điểm E sao cho IE = IB. Khẳng định nào sau đây đúng?

A. AE = BC;

B. AE // BC;

C. ∆AIE = ∆CIB;

D. Cả A, B và C đều đúng.

Hướng dẫn giải

Đáp án: D

Giải thích:

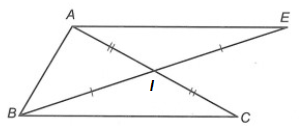
TOP 20 câu Trắc Nghiệm Trường hợp bằng nhau thứ hai và thứ ba của tam giác - Toán 7 Kết nối tri thức (ảnh 1)

⦁ Xét ∆AIE và ∆CIB, có:

AI = CI (I là trung điểm của AC)

IE = IB (giả thiết)

$\hat{A I E} = \hat{B I C}$ (hai góc đối đỉnh)

Do đó ∆AIE = ∆CIB (c.g.c)

Vì vậy phương án C đúng.

⦁ Ta có ∆AIE = ∆CIB (chứng minh trên)

Suy ra AE = BC và $\hat{E A I} = \hat{I C B}$ (cặp cạnh và cặp góc tương ứng)

Vì vậy phương án A đúng.

⦁ Ta có $\hat{E A I} = \hat{I C B}$ (chứng minh trên)

Mà hai góc này ở vị trí so le trong.

Suy ra AE // BC.

Do đó phương án B đúng.

Vậy ta chọn phương án D.

Câu 3. Cho hình vẽ sau. Biết AB // CD và AD // BC.

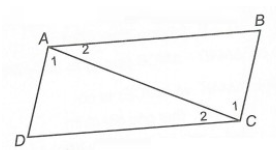
TOP 20 câu Trắc Nghiệm Trường hợp bằng nhau thứ hai và thứ ba của tam giác - Toán 7 Kết nối tri thức (ảnh 1)

Hình vẽ trên có mấy cặp tam giác bằng nhau?

A. 0;

B. 1;

C. 2;

D. 3.

Hướng dẫn giải

Đáp án: B

Giải thích:

Xét ∆ABC và ∆CDA, có:

AC là cạnh chung.

$\hat{A_{1}} = \hat{C_{1}}$ (do AD // BC và hai góc này ở vị trí so le trong)

$\hat{A_{2}} = \hat{C_{2}}$ (do AB // DC và hai góc này ở vị trí so le trong)

Do đó ∆ABC = ∆CDA (g.c.g)

Vậy có 1 cặp tam giác bằng nhau.

Do đó ta chọn phương án B.

Câu 4. Cho ∆ABC, điểm M thuộc cạnh BC. Đường thẳng đi qua M và song song với AB cắt AC ở D. Đường thẳng đi qua M và song song với AC cắt AB ở E.

Cho các khẳng định dưới đây:

(I) $\hat{A D M} = \hat{A E M}$ ;

(II) ME = AD;

(III) ∆AMD = ∆MAE.

Có bao nhiêu khẳng định đúng?

A. 0;

B. 1;

C. 2;

D. 3.

Hướng dẫn giải

Đáp án: D

Giải thích:

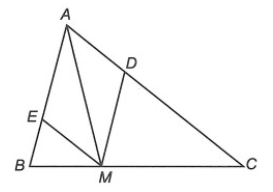
TOP 20 câu Trắc Nghiệm Trường hợp bằng nhau thứ hai và thứ ba của tam giác - Toán 7 Kết nối tri thức (ảnh 1)

Xét ∆AMD và ∆MAE, có:

AM là cạnh chung.

$\hat{A M D} = \hat{M A E}$ (MD // AE)

$\hat{M A D} = \hat{A M E}$ (ME // AD)

Do đó ∆AMD = ∆MAE (g.c.g)

Suy ra ME = AD và $\hat{A D M} = \hat{A E M}$ (cặp cạnh và cặp góc tương ứng).

Do đó (I), (II), (III) đều đúng.

Vậy ta chọn phương án D.

Câu 5. Cho tam giác ABC cân tại A, có $\hat{A} = 24 °$ . Trên tia đối của tia BC lấy điểm D sao cho $\hat{A D B} = 30 °$ , trên tia đối của tia CB lấy điểm E sao cho BD = CE. Tính $\hat{B A E}$ ?

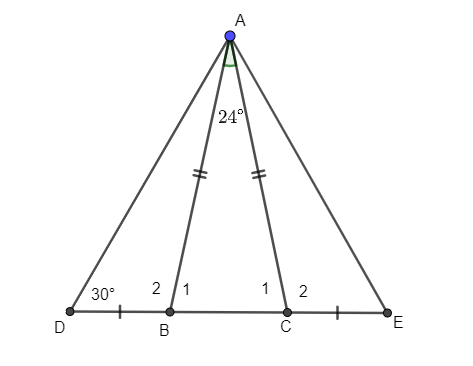
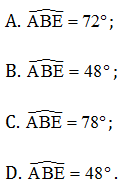
TOP 20 câu Trắc Nghiệm Trường hợp bằng nhau thứ hai và thứ ba của tam giác - Toán 7 Kết nối tri thức (ảnh 1)

Hướng dẫn giải

Đáp án: A

Giải thích:

TOP 20 câu Trắc Nghiệm Trường hợp bằng nhau thứ hai và thứ ba của tam giác - Toán 7 Kết nối tri thức (ảnh 1)

$\hat{B A E} = 180 ° - \hat{B_{1}} - \hat{E} = 180 ° - 78 ° - 30 ° = 72 °$

Vậy ta chọn phương án A.

Câu 6. Cho hình vẽ bên. Biết rằng AB = AC.

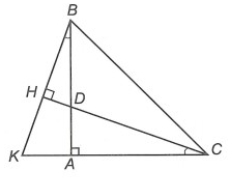
TOP 20 câu Trắc Nghiệm Trường hợp bằng nhau thứ hai và thứ ba của tam giác - Toán 7 Kết nối tri thức (ảnh 1)

Kết luận nào sau đây đúng?

A. ∆ABK = ∆ACD;

B. $\hat{A K B} \neq \hat{A D C}$ ;

C. CD < BK;

D. AK > AD.

Hướng dẫn giải

Đáp án: A

Giải thích:

Xét ∆ABK và ∆ACD, có:

AB = AC (giả thiết)

$\hat{B A K} = \hat{C A D} = 90 °$ .

$\hat{A B K} = \hat{A C D}$ (giả thiết)

Do đó ∆ABK = ∆ACD (g.c.g)

Suy ra $\hat{A K B} = \hat{A D C}$ , BK = CD và AK = AD (các cặp góc và cặp cạnh tương ứng)

Vì vậy phương án A đúng, phương án B, C, D sai.

Vậy ta chọn phương án A.

Câu 7. Cho hai tam giác ABC và DEF thỏa mãn AB = DE, $\hat{A B C} = \hat{DEF}$ , $\hat{B A C} = \hat{E D F}$ , AB = 5cm, AC = 6cm, EF = 8cm. Nửa chu vi p tam giác DEF nằm trong khoảng nào dưới đây:

A. 9 < p < 10;

B. 15 < p < 19;

C. 19 < p < 20;

D. 25 < p < 29.

Hướng dẫn giải

Đáp án: A

Giải thích:

Xét ∆ABC và ∆DEF, có:

$\hat{A B C} = \hat{DEF}$ (gt)

AB = DE (giả thiết)

$\hat{B A C} = \hat{E D F}$ (gt)

Do đó ∆ABC = ∆DEF (g.c.g)

⇒ AB = DE = 5cm, AC = DF = 6cm

Khi đó chu vi của tam giác DEF là: 5 + 6 + 8 = 19 cm.

Nửa chu vi của tam giác DEF là: 19 : 2 = 9,5 cm.

Vì vậy 9 < p < 10.

Vậy chọn đáp án A.

Từ khóa :

Giải bài tập Toán 7

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

226

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

262

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

286

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

236