Toptailieu.vn biên soạn và giới thiệu Lý thuyết Đại lượng tỉ lệ nghịch (Kết nối tri thức) Toán 7 hay, ngắn gọn và bài tập tự luyện có lời giải chi tiết sẽ giúp học sinh nắm vững nội dung kiến thức từ đó dễ dàng làm các bài tập Toán 7.
Nội dung bài viết
Lý thuyết Đại lượng tỉ lệ nghịch (Kết nối tri thức) Toán 7
A. Lý thuyết
1. Đại lượng tỉ lệ nghịch
• Nếu đại lượng y liên hệ với đại lượng x theo công thức y=axy=ax(a là một hằng số khác 0) thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ a.
Chú ý:
Nếu y tỉ lệ nghịch với x theo hệ số tỉ lệ a thì x cũng tỉ lệ nghịch với y theo hệ số tỉ lệ a và ta nói hai đại lượng x và y tỉ lệ nghịch với nhau.
Ví dụ: Nếu y=3xy=3x thì y tỉ lệ nghịch với x theo hệ số 3, hay x tỉ lệ nghịch với y theo hệ số 3.
Nhận xét:
Nếu hai đại lượng y và x tỉ lệ nghịch với nhau thì:
• Tích hai giá trị tương ứng của chúng luôn không đổi (và bằng hệ số tỉ lệ):
x1y1=x2y2=x3y3=...=ax1y1=x2y2=x3y3=...=a hay y11x1=y21x2=y31x3=...=ay11x1=y21x2=y31x3=...=a
• Tỉ số hai giá trị bất kì của đại lượng này bằng nghịch đảo của tỉ số hai giá trị tương ứng của đại lượng kia:
y1y2=x2x1;y1y3=x3x1;y2y3=x3x2;...y1y2=x2x1;y1y3=x3x1;y2y3=x3x2;...
Ví dụ: Cho biết x và y là hai đại lượng tỉ lệ nghịch. Điền số thích hợp vào ô trống trong bảng sau:
|
x |
0,5 |
-1,2 |
4 |
6 |
||
|
y |
3 |
-2 |
1,5 |
Hướng dẫn giải:
Gọi hệ số tỉ lệ của x và y là a, nghĩa là y=axy=ax hay x . y = a.
Ta có x = 4 thì y = 1,5 nên suy ra a = x.y = 4 . 1,5 = 6.
Vậy x . y = 6.
Khi x = 0,5 thì y = 6 : 0,5 = 12
Khi x = -1,2 thì y = 6 : (-1,2) = -5
Khi y = 3 thì x = 6 : 3 = 2
Khi y = -2 thì x = 6 : (-2) = -3
Khi x = 6 thì y = 6 : 6 = 1
Vậy ta có bảng sau:
|
x |
0,5 |
-1,2 |
2 |
-3 |
4 |
6 |
|
y |
12 |
-5 |
3 |
-2 |
1,5 |
1 |
2. Một số bài toán về đại lượng tỉ lệ nghịch
Để giải toán về đại lượng tỉ lệ nghịch, ta cần nhận biết được hai đại lượng tỉ lệ nghịch trong bài toán. Từ đó ta có thể lập các tỉ số bằng nhau và dựa vào tính chất của dãy tỉ số bằng nhau để tìm các yếu tố chưa biết.
Ví dụ:
Cho biết 35 công nhân xây một ngôi nhà hết 168 ngày. Hỏi 28 công nhân xây một ngôi nhà trong bao nhiêu ngày? (Giả sử năng suất làm việc của mỗi công nhân là như nhau)
Hướng dẫn giải:
Vì năng suất làm việc của mỗi người là như nhau nên số công nhân và số ngày xây xong ngôi nhà là hai đại lượng tỉ lệ nghịch.
Gọi số công nhân là y (công nhân); số ngày xây xong ngôi nhà là x (ngày). (y ∈ℕ*; x > 0)
Ta có x . y = a
Khi y = 35 thì x = 168 nên ta có a = 35 . 168 = 5880.
Do đó x . y = 5880.
Vậy khi y = 28 thì x = 5880 : 28 =210.
Vậy 28 công nhân xây ngôi nhà đó hết 210 ngày.
Bài 1. Hai đại lượng x và y có tỉ lệ nghịch với nhau hay không, nếu:
a)
|
x |
1 |
2 |
4 |
5 |
8 |
|
y |
120 |
60 |
30 |
24 |
15 |
b)
|
x |
2 |
3 |
4 |
5 |
6 |
|
y |
30 |
20 |
15 |
12,5 |
10 |
Hướng dẫn giải:
a) Ta có 1 . 20 = 2 . 60 = 4 . 30 = 5 . 24 = 8 . 15 = 120.
Nên x và y là hai đại lượng tỉ lệ nghịch với nhau.
b) Vì 5 . 12,5 ≠ 6 . 10 nên x và y không tỉ lệ nghịch với nhau.
Bài 2. Cho biết hai đại lượng x và y tỉ lệ nghịch với nhau. Điền số thích hợp vào ô trống:
|
x |
1 |
-8 |
10 |
|||
|
y |
8 |
-4 |
1,6 |
Hướng dẫn giải:
Nhìn vào bảng ta thấy khi x = 10 thì y = 1,6. Do đó hệ số tỉ lệ a = 10 . 1,6 = 16.
Vậy x . y = 16.
Do đó:
Khi x = 1 thì y = 16 : 1 = 16
Khi y = 8 thì x = 16 : 8 = 2
Khi y = -4 thì x = 16: (-4) = -4
Khi y = 223⇒x=16:223=16:83=16.38=6
Khi x = -8 thì y = 16 : (-8) = -2.
Từ đó ta có bảng sau :
|
x |
1 |
2 |
-4 |
6 |
-8 |
10 |
|
y |
16 |
8 |
-4 |
-2 |
1,6 |
Bài 3. Cho biết 3 người làm cỏ một cánh đồng hết 6 giờ. Hỏi 12 người (có cùng năng suất) làm cỏ cánh đồng đó hết bao nhiêu thời gian?
Hướng dẫn giải:
Với cùng một cánh đồng nên số người làm cỏ hết cánh đồng đó và số giờ là hai đại lượng tỉ lệ nghịch.
Hệ số tỉ lệ bằng 3 . 6 = 18.
Gọi số giờ để 12 người làm cỏ hết cánh đồng là x (giờ) (x > 0)
Theo tính chất của đại lượng tỉ lệ nghịch ta có x . 12 = 18 suy ra x = 18 : 12 = 1,5.
Vậy 12 người làm cỏ cánh đồng hết 1,5 giờ (1 giờ 30 phút).
Bài 4. Với cùng số tiền để mua 51 mét vải loại I có thể mua được bao nhiêu mét vải loại II, biết rằng giá tiền 1 mét vải loại II chỉ bằng 85% giá tiền vải loại I?
Hướng dẫn giải:
Gọi giá tiền 1 mét vải loại I là x1; giá tiền 1m vải loại II là x2.
Với cùng một số tiền, số mét vải loại I và loại II mua được tương ứng là y1; y2 (m).
Theo đề bài có: y1 = 51; x2 = 85%.x1 = 0,85.x1.
Với cùng một số tiền thì giá tiền 1 mét vải và số vải mua được là hai đại lượng tỉ lệ nghịch nên ta có:
x1.y1=x2.y2⇒x1x2=y2y1
Mà x1x2=x10,85.x1=10,85=2017;y1=51⇒y2=51.2017=60(m)
Vậy với cùng số tiền đó ta có thể mua được 60m vải loại II.
B. Trắc nghiệm Đại lượng tỉ lệ nghịch (Kết nối tri thức 2023) có đáp án
Câu 1. Cho biết đại lượng y tỉ lệ nghịch với đại lượng x theo hệ số tỉ lệ a ( a khác 0) . Hãy biểu diễn y theo x.
A. y = xa;
B. y = –ax;
C. y = ax;
D. y = ax.
Hướng dẫn giải
Đáp án: D
Giải thích:
Đại lượng y tỉ lệ nghịch với đại lượng x theo hệ số tỉ lệ a nên y liên hệ với x theo công thức y = ax với a khác 0.
Vậy đáp án đúng là D.
Câu 2. Chọn câu đúng. Nếu y = ax ( a khác 0 ) thì ta nói
A. y tỉ lệ nghịch với x theo hệ số tỉ lệ a;
B. y tỉ lệ thuận với x theo hệ số tỉ lệ a;
C. x tỉ lệ thuận với y theo hệ số tỉ lệ a;
D. Cả 3 đáp án trên đều sai.
Hướng dẫn giải
Đáp án: A
Giải thích:
Nếu đại lượng y liên hệ với đại lượng x theo công thức y = ax với a khác 0 thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ a ( nhận biết đại lượng tỉ lệ nghịch).
Vậy đáp án đúng là A.
Câu 3. Chọn câu đúng. Nếu y = 5x thì ta nói
A. y tỉ lệ nghịch với x theo hệ số tỉ lệ 5;
B. y tỉ lệ thuận với x theo hệ số tỉ lệ 5;
C. y tỉ lệ nghịch với x theo hệ số tỉ lệ 15;
D. Không kết luận được điều gì về x và y.
Hướng dẫn giải
Đáp án: A
Giải thích:
Nếu đại lượng y liên hệ với đại lượng x theo công thức y = ax với a khác 0 thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ a ( nhận biết đại lượng tỉ lệ nghịch).
Như vậy nếu đại lượng y liên hệ với đại lượng x theo công thức y = 5x thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ 5.
Vậy chọn đáp án A.
Câu 4. Cho biết đại lượng x tỉ lệ nghịch với đại lượng y theo hệ số tỉ lệ –3. Hãy biểu diễn y theo x.
A. y = –3x;
B. y = −3x;
C. y = 3x;
D. y = 13x.
Hướng dẫn giải
Đáp án: B
Giải thích:
Nếu đại lượng y liên hệ với đại lượng x theo công thức y = ax với a khác 0 thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ a ( nhận biết đại lượng tỉ lệ nghịch).
Như vậy nếu đại lượng y liên hệ với đại lượng x theo công thức y = -3x thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ –3.
Vậy chọn đáp án B.
Câu 5. Chọn câu đúng. Nếu y = −2x thì ta nói:
A. y tỉ lệ nghịch với x theo hệ số tỉ lệ –2;
B. y tỉ lệ nghịch với x theo hệ số tỉ lệ –12;
C. y tỉ lệ thuận với x theo hệ số tỉ lệ –12;
D. y tỉ lệ thuận với x theo hệ số tỉ lệ –2.
Hướng dẫn giải
Đáp án: A
Giải thích:
Nếu đại lượng y liên hệ với đại lượng x theo công thức y = ax với a khác 0 thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ a ( nhận biết đại lượng tỉ lệ nghịch).
Như vậy nếu đại lượng y liên hệ với đại lượng x theo công thức y = -2x thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ –2.
Vậy chọn đáp án A.
II. Thông hiểu
Câu 1. Biết rằng x và y tỉ lệ nghịch với nhau và khi x = 2 thì y = 4. Tìm hệ số tỉ lệ.
A. 2;
B. 8;
C. 4;
D. 1.
Hướng dẫn giải
Đáp án: B
Giải thích:
Do x và y tỉ lệ nghịch với nhau nên đại lượng y liên hệ với đại lượng x qua công thức
y = ax với a khác 0.
Theo đề bài khi x = 2 thì y = 4 nên thay vào công thức ta có 4 = a2 hay a = 8.
Vậy x và y tỉ lệ nghịch với nhau với hệ số tỉ lệ là 8.
Câu 2. Biết rằng x và y tỉ lệ nghịch với nhau và khi x = 5 thì y = 4. Tìm giá trị tương ứng của y khi x = 4.
A. 8;
B. 6;
C. 3;
D. 5.
Hướng dẫn giải
Đáp án: D
Giải thích:
Do x và y tỉ lệ nghịch với nhau nên đại lượng y liên hệ với đại lượng x qua công thức
y = ax với a khác 0.
Theo đề bài khi x = 5 thì y = 4 nên thay vào công thức ta có 4 = a5 hay a = 20.
Ta được công thức y = 20x. Khi x = 4 thì y = 204 = 5.
Vậy khi x = 4 thì y = 5. Chọn đáp án D.
Câu 3. Cho x và y là hai đại lượng tỉ lệ nghịch. Gọi x1 , x2 là hai giá trị của x, gọi y1, y2 là hai giá trị của y. Biết 2x1 – 3y2 = 22 và y1 = 5, x2 = 2. Biểu diễn y theo x.
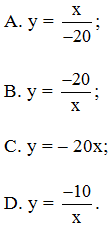
Hướng dẫn giải
Đáp án: B
Giải thích:
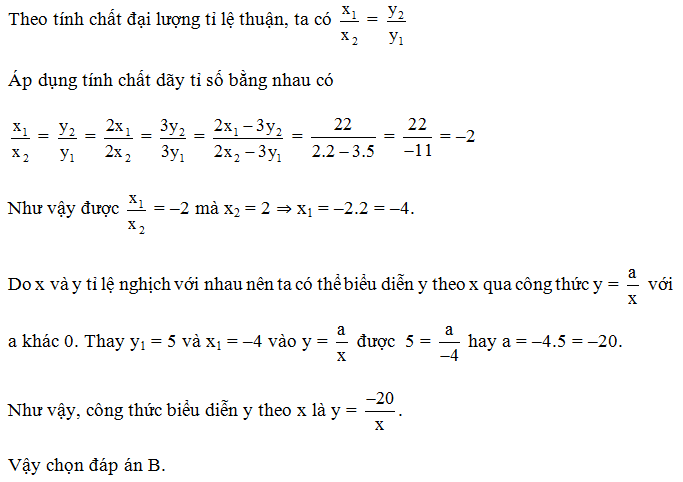
Câu 4. Cho x và y tỉ lệ nghịch và khi x = 3 thì y = 7. Biểu diễn y theo x.
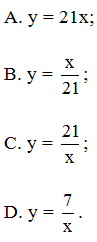
Hướng dẫn giải
Đáp án: C
Giải thích:
Do x và y tỉ lệ nghịch với nhau nên ta có thể biểu diễn y theo x qua công thức y = ax với a khác 0. Thay y = 7 và x = 3 vào y = ax được 7 = a3 hay a = 3.7 = 21.
Như vậy, công thức biểu diễn y theo x là y = 21x.
Chọn đáp án C.
Câu 5. Cho biết y tỉ lệ nghịch với x theo hệ số tỉ lệ 4 và x tỉ lệ nghịch với z theo hệ số tỉ lệ 74. Chọn câu đúng
A. y tỉ lệ thuận với z theo hệ số tỉ lệ 716;
B. y tỉ lệ thuận với z theo hệ số tỉ lệ 167;
C. y tỉ lệ nghịch với z theo hệ số tỉ lệ 716;
D. y tỉ lệ nghịch với z theo hệ số tỉ lệ 167 .
Hướng dẫn giải
Đáp án: B
Giải thích:
Do y tỉ lệ nghịch với x theo hệ số tỉ lệ 4 nên y = 4x.
Do x tỉ lệ nghịch với z theo hệ số 74 nên x = 74z.
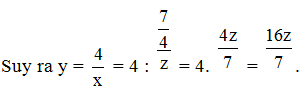
Như vậy y = 16z7. Ta nói y tỉ lệ thuận với z theo hệ số tỉ lệ 167.
Chọn đáp án B.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.