Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Bài tập về hàm số, đồ thị và các vấn đề liên quan (HAY NHẤT 2024) gồm đầy đủ các phần ý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh nắm vững lý thuyết, biết cách giải các dạng bài tập Bài tập về hàm số, đồ thị và các vấn đề liên quan từ đó có kế hoạch ôn tập hiệu quả để đạt kết quả cao trong các bài thi môn Toán.
Phương pháp giải Bài tập về hàm số, đồ thị và các vấn đề liên quan (HAY NHẤT 2024)
I. Hàm số
Định nghĩa:
Giả sử x và y là hai đại lượng biến thiên,
Nếu với mỗi , ta xác định được y duy nhất () thì ta có một hàm số.
Tên gọi:
x là biến số, y là hàm số của x
D là tập xác định
là tập giá trị của hàm số.
+) Ta thường kí hiệu là giá trị y tương ứng với x, nên hàm số thường viết là
Chú ý:
a. Hàm số cho bởi công thức mà không chỉ rõ tập xác định thì
TXĐ của hàm số là tập hợp tất cả các sao cho có nghĩa.
b. Một hàm số có thể được cho bởi hay nhiều công thức.
Hệ thống bài tập tự luận
Dạng 1. Tìm tập xác định của hàm số
Phương pháp: Để tìm tập xác định D của hàm số y = f(x) ta tìm điều kiện của x để f(x) có nghĩa.
Chú ý: Thông thường y = f(x) cho bởi biểu thức đại số, ta xét một số trường hợp sau:
+ Hàm số y = f(x) = có nghĩa khi u(x), v(x) có nghĩa và v(x)
+ Hàm số y = f(x) = có nghĩa khi u(x) có nghĩa và u(x)
+ Hàm số y = f(x) = có nghĩa khi u(x), v(x) có nghĩa và v(x) > 0
Bài tập: Tìm tập xác định của hàm số y =
Lời giải:
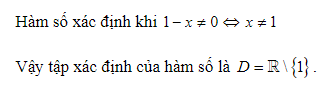
Dạng 2. Tìm điều kiện để hàm số xác định trên một tập K cho trước
Phương pháp:
Bài toán: Cho hàm y = f(x, m). Tìm tất cả các giá trị của m để hàm số xác định trên tập K.
Bước 1: Tìm điều kiện xác định của hàm số (theo m). Gọi D là tập xác định của hàm số.
Bước 2: Hàm số xác định trên tập K khi và chỉ khi KD.
Một số lưu ý:
+ Hàm số y = (A là biểu thức luôn có nghĩa) xác định trên tập K khi và chỉ khi phương trình f(x, m) = 0 vô nghiệm trên K.
+ Hàm số y = xác định trên tập K khi và chỉ khi bất phương trình f(x, m)0 nghiệm đúng với mọi x K.
+ Hàm số y = (A là biểu thức luôn có nghĩa) xác định trên tập K khi và chỉ khi bất phương trình f(x, m) > 0 nghiệm đúng với mọi x K.
+ K (D1D2)<=>
Bài tập: Cho hàm số y = . Tìm tất cả các giá trị của m để hàm số xác định trên .
Lời giải:
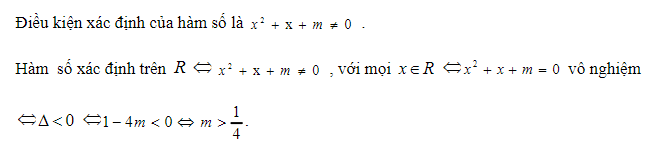
Dạng 3. Tập giá trị của hàm số
Phương pháp: Cho hàm số y = f(x) có tập xác định D.
Tập hợp T = {y = f(x)x D} gọi là tập giá trị của hàm số y = f(x).
Bài tập: Tìm tập giá trị của hàm số y = 5x - 4
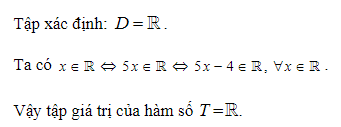
Dạng 4. Tính đồng biến, nghịch biến của hàm số
Phương pháp 1:
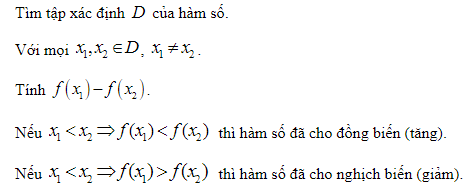
Phương pháp 2:

Bài tập: Xét tính đồng biến và nghịch biến của hàm số f(x) = x2 - 7 trên khoảng (-;0) và trên khoảng (0;+)
Lời giải:

Dạng 5. Tìm điều kiện của tham số để hàm số đồng biến (nghịch biến) trên một tập hợp cho trước
Phương pháp:
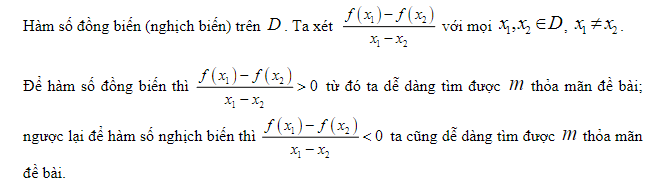
Bài tập: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-3; 3] để hàm số f(x) = (m + 1)x + m - 2 đồng biến trên ?
Lời giải:
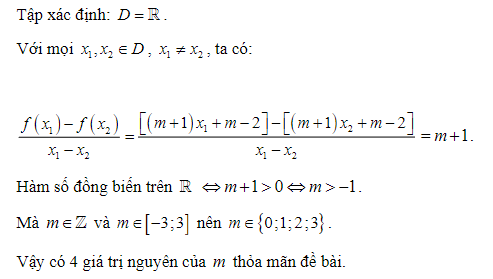
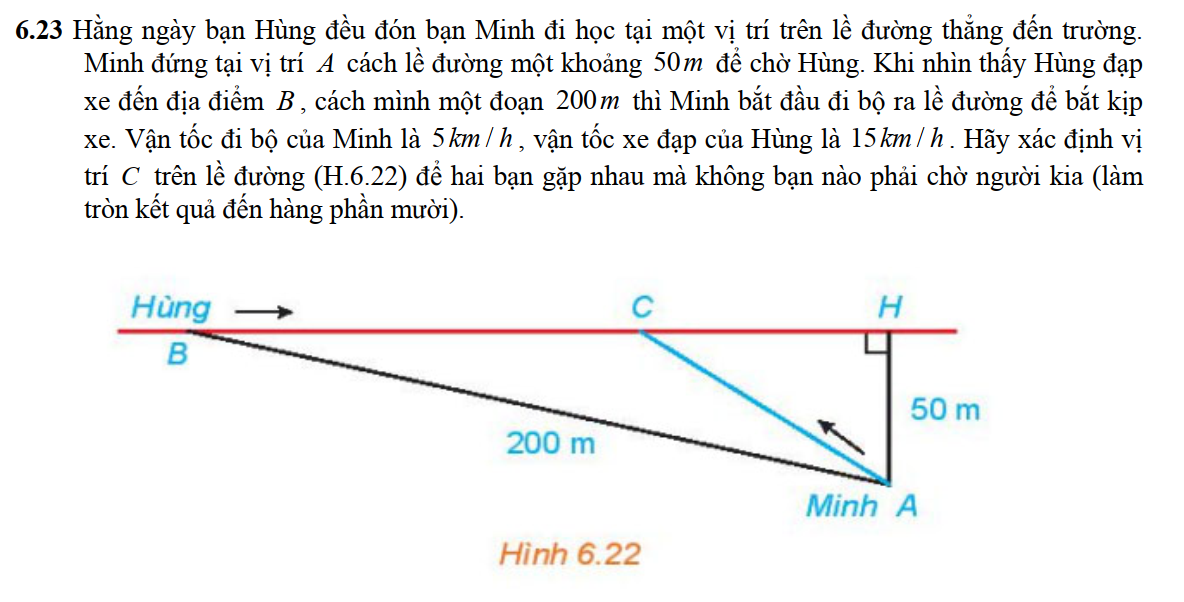
Dạng 6. Bài toán thực tế
Phương pháp:
Bước 1: Lập biểu thức theo yêu cầu bài toán (nếu cần)
Bước 2: Khai thác giả thiết để xử lí bài toán phù hợp
Bước 3: Kết luận
Bài tập: Cho rằng diện tích rừng nhiệt đới trên trái đất được xác định bởi hàm số S = 718,3 - 4,6t, trong đó S được tính bằng triệu hec-ta, t tính bằng số năm kể từ năm 1990. Hãy tính diện tích rừng nhiệt đới vào các năm 1990 và 2018.
Lời giải:

Hệ thống bài tập trắc nghiệm
Dạng 1. Tập xác định của hàm số

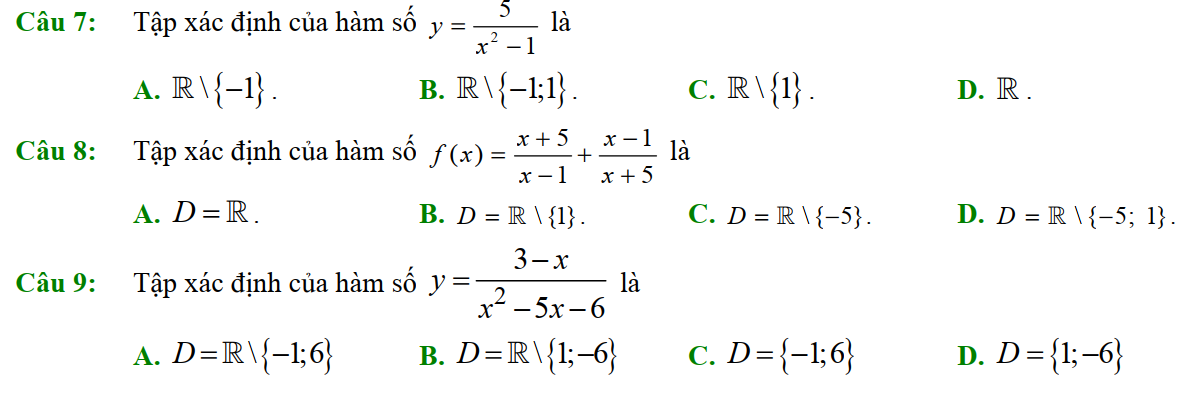
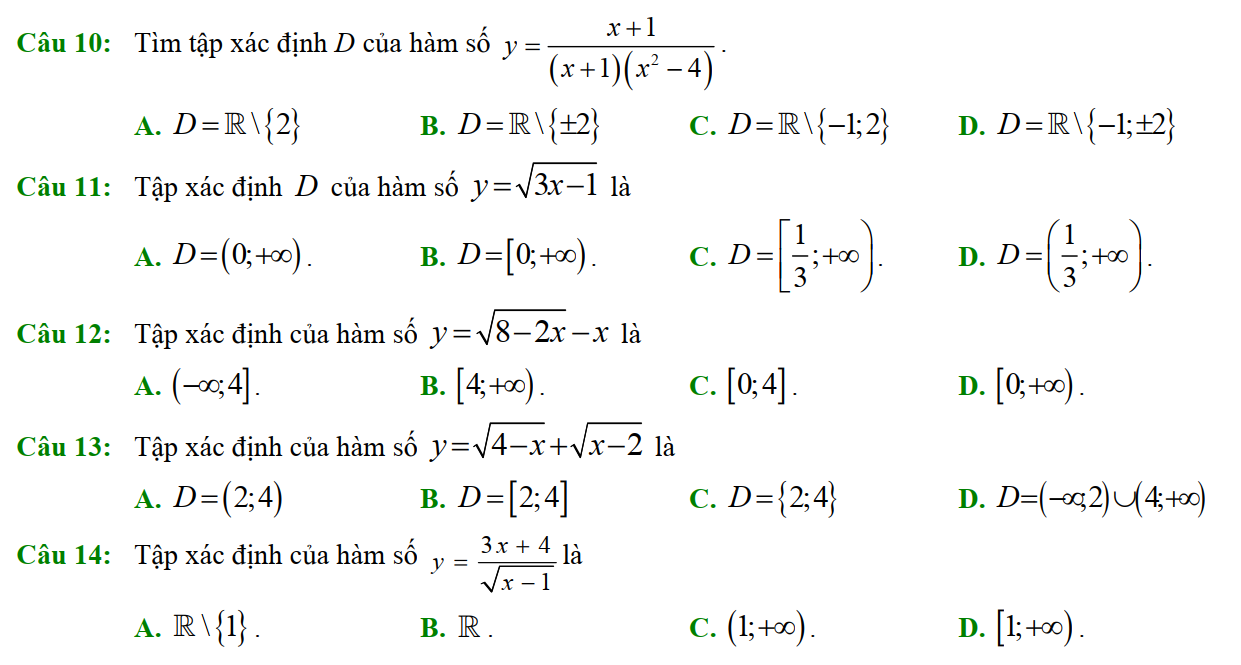

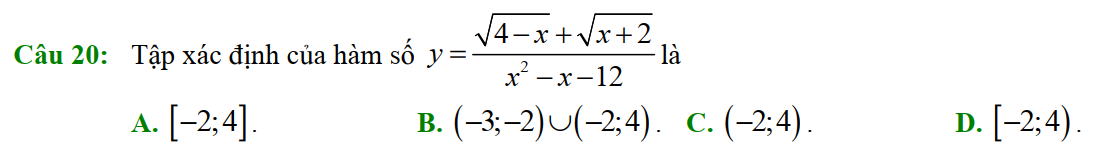
Dạng 2. Xác định sự biến thiên của hàm số cho trước


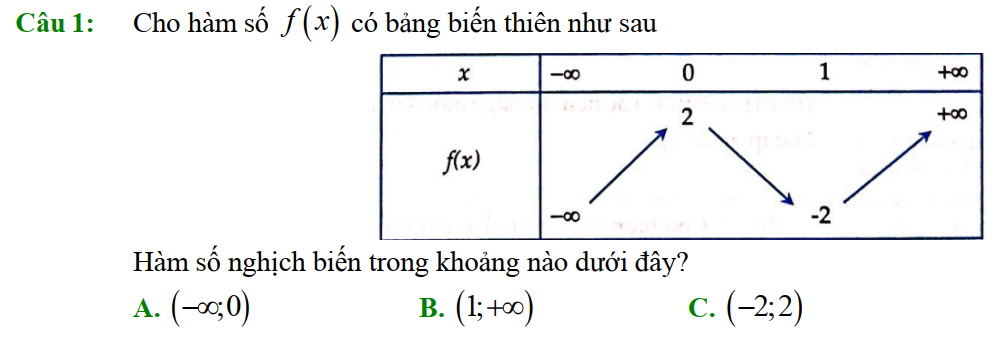
Dạng 3. Xác định sự biến thiên thông qua đồ thị của hàm số



Dạng 4. Một số bài toán liên quan đến đồ thị của hàm số

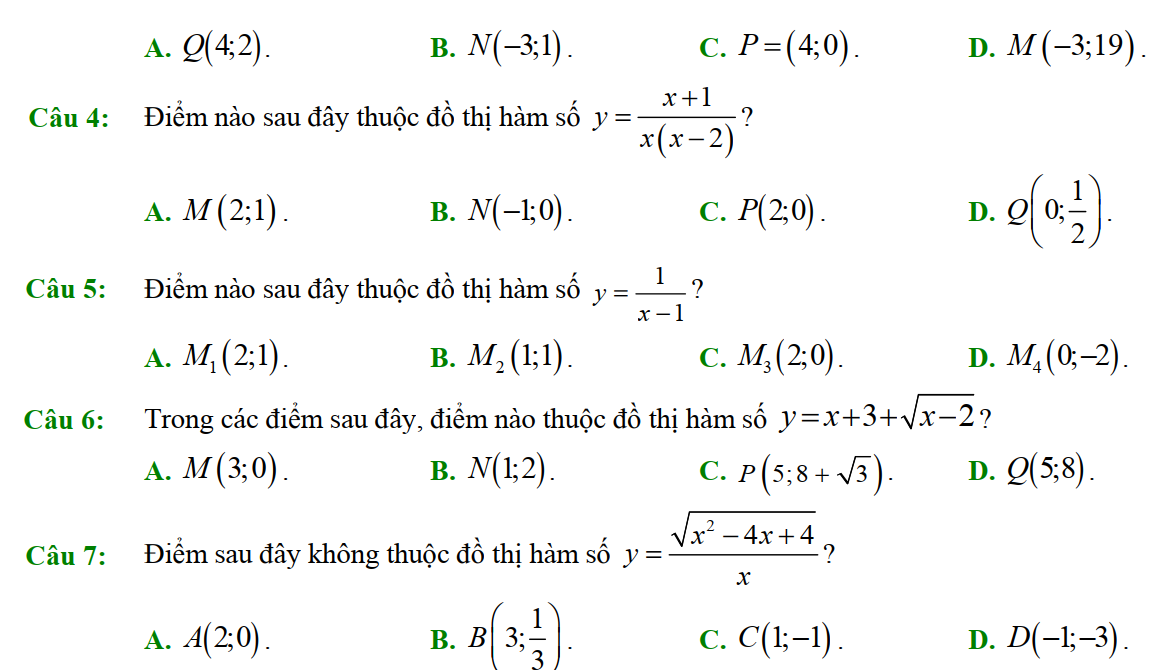
II. Hàm số bậc hai
Định nghĩa:
Hàm số bậc hai được cho bởi công thức:
có tập xác định và biệt thức
Chiều biến thiên:
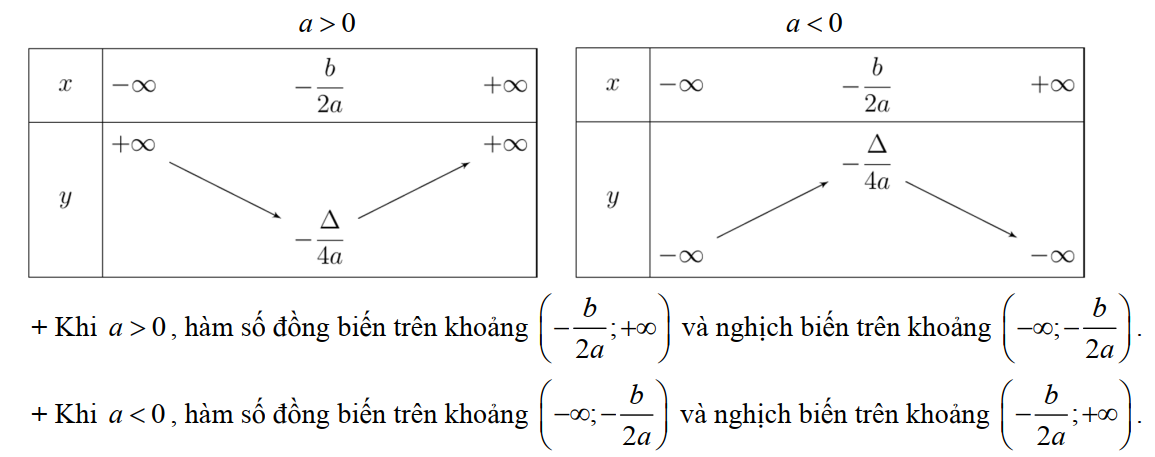
Nếu thì hàm số :
+) Nghịch biến trên khoảng
+) Đồng biến trên khoảng
Hàm số đạt có điểm cực tiểu là
Nếu thì hàm số :
+) Đồng biến trên khoảng
+) Nghịch biến trên khoảng
Hàm số đạt có điểm cực đại là
Đồ thị của hàm số bậc hai:

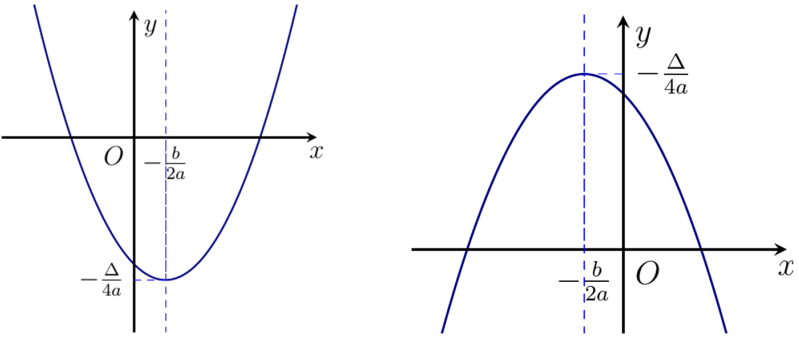
Bảng biến thiên:

Hệ thống bài tập tự luận
Vấn đề 1. Tìm điều kiện để hàm số y = ax2 + bx + c đồng biến trên khoảng (a;b)
Phương pháp:
+ Trường hợp a = 0 : Yêu cầu bài toán
+ Trường hợp a > 0 : Yêu cầu bài toán
+ Trường hợp a < 0 : Yêu cầu bài toán
Bài tập:
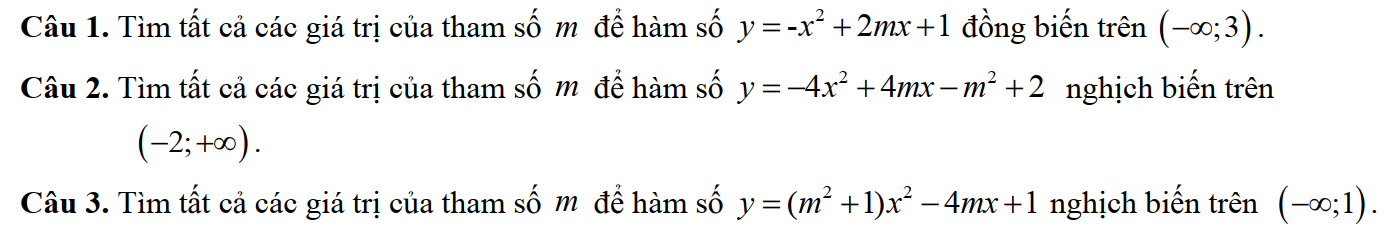
Vấn đề 2. Xác định hàm số bậc hai
Phương pháp:

Bài tập:
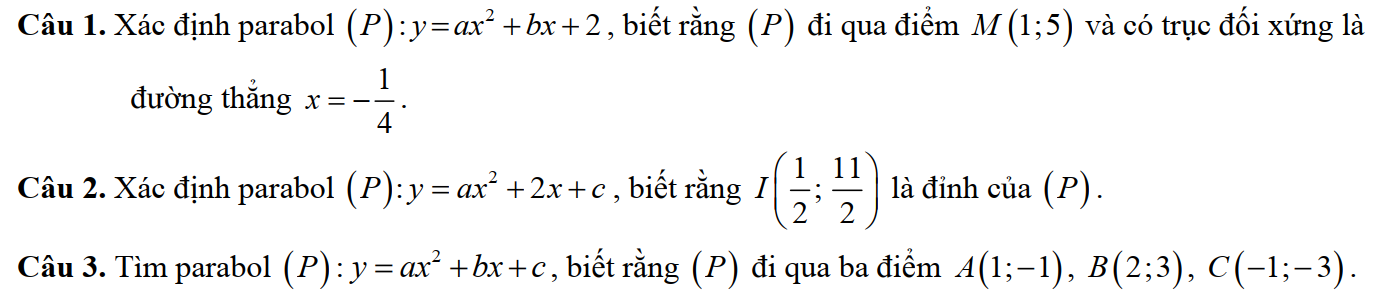
Vấn đề 3. Đồ thị hàm số bậc hai
Dạng 1: Cho parabol (P) : y = ax2 + bx + c
+ Xác định trục đối xứng, tọa độ đỉnh của (P)
+ Tương giao của (P) với trục Ox
+ Tìm điều kiện để các giao điểm của (P) và trục Ox thỏa mãn điều kiện nào đó
Phương pháp:

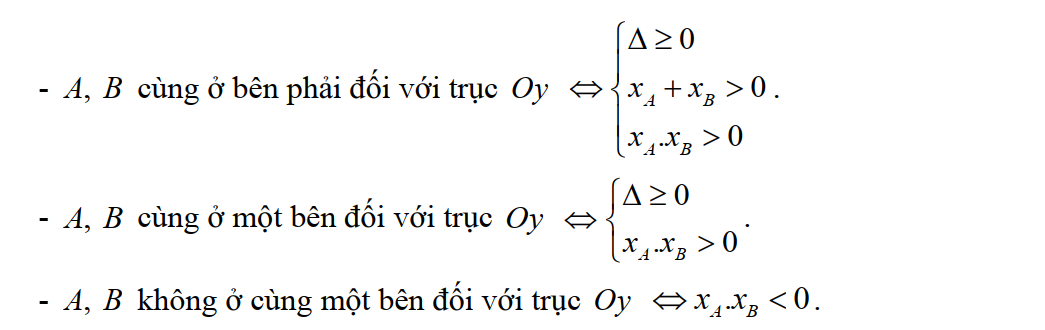
Bài tập:

Dạng 2: Cho parabol (P) : y = ax2 + bx + c và đường thẳng d : y = mx + n
+ Biện luận số điểm chung của (P) và trục hoành
+ Tìm điều kiện để đường thẳng d tiếp xúc với (P)
Phương pháp:

Bài tập:
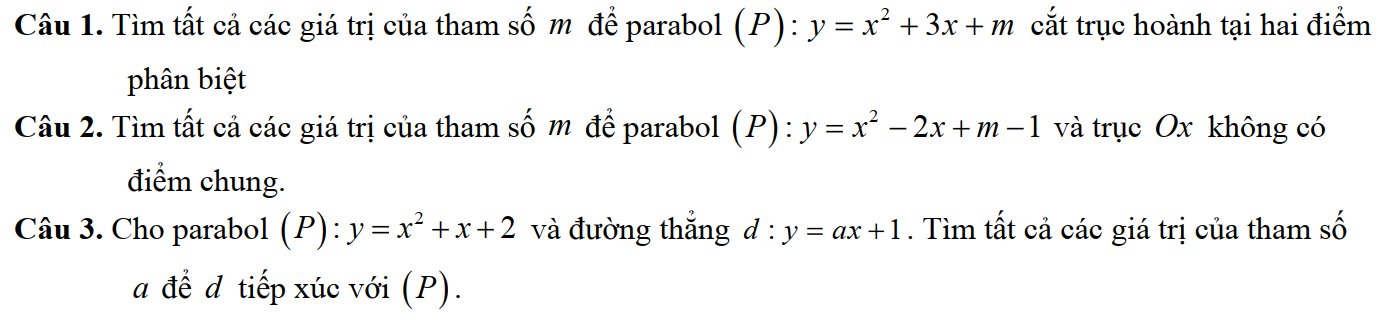
Vấn đề 4. Tương giao đồ thị
Dạng 1: Dựa vào đồ thị hàm số f(x) để biện luận theo tham số m số nghiệm của phương trình f(x) =g(m)
Phương pháp:

Bài tập:
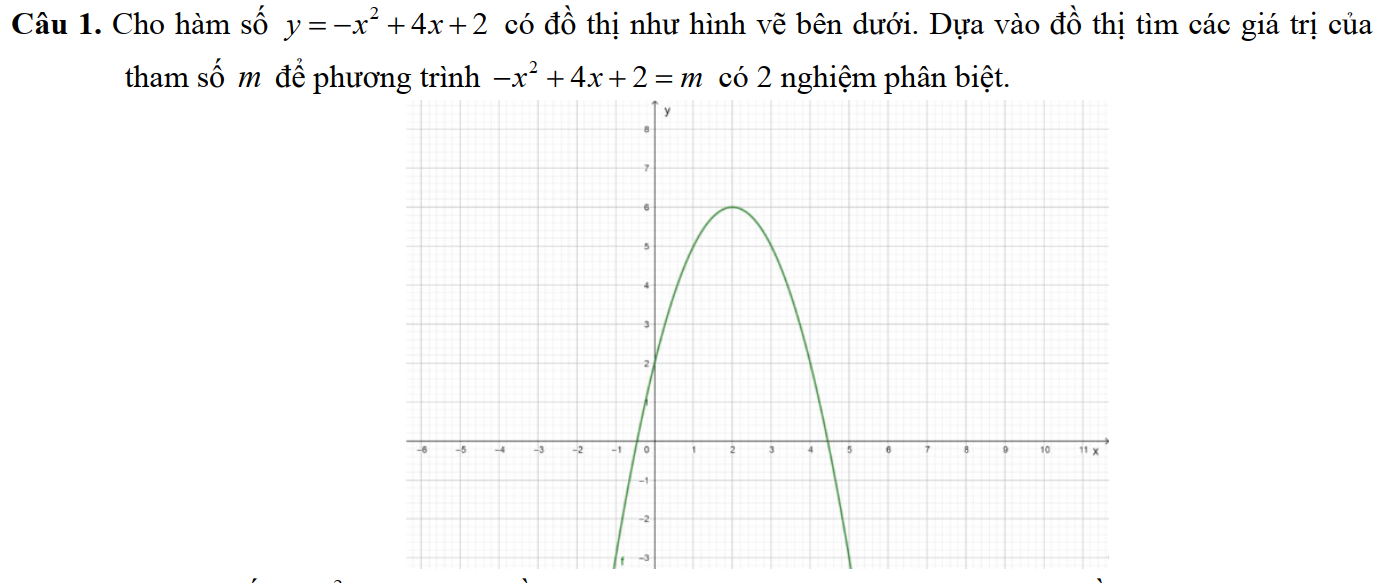
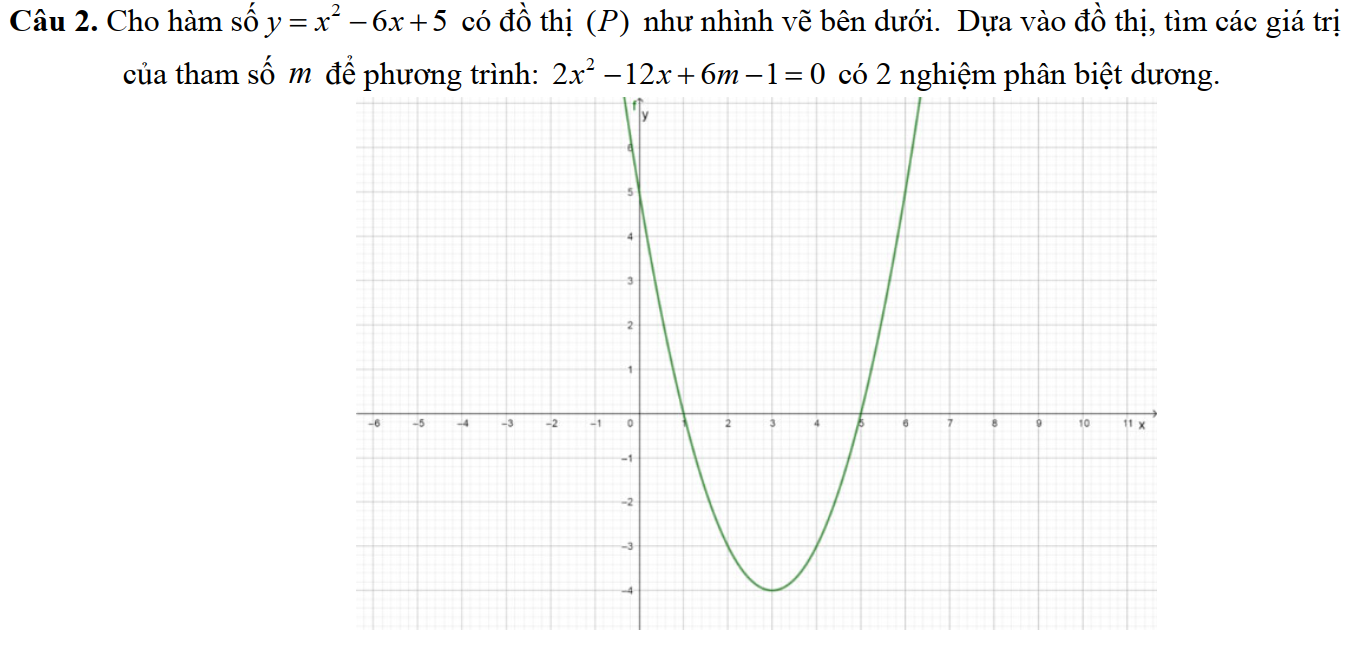
Dạng 2: Sự tương giao của đồ thị hàm số bậc nhất và bậc hai
Phương pháp:

Nhận xét:
+ Số giao điểm của (P) và d bằng số nghiệm của hệ phương trình (1) và cũng bằng số nghiệm của phương trình (2)
+ Nếu phương trình (2) vô nghiệm thì ta nói d và (P) không giao nhau
+ Nếu phương trình (2) có nghiệm kép thì ta nói d và (P) tiếp xúc với nhau. Lúc này ta nói d là tiếp tuyến của (P)
+ Nếu phương trình (2) có 2 nghiệm phân biệt thì ta nói d và (P) cắt nhau
Bài tập:
![]()

Dạng 3: Sự tương giao của hai đồ thị hàm số bậc hai
Phương pháp:

Bài tập:

Vấn đề 5. Điểm cố định của đồ thị hàm số
Phương pháp:

Bài tập:
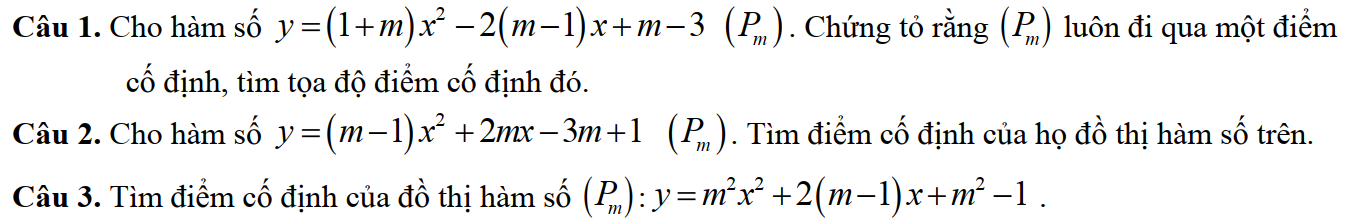
Vấn đề 6. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số bậc hai
Dạng 1: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên 1 tập cho trước
Phương pháp:

Bài tập:

Dạng 2: Tìm điều kiện của tham số để hàm số bậc hai đạt giá trị lớn nhất, giá trị nhỏ nhất
Phương pháp:
Cho hàm số bậc hai: y = ax2 + bx + c (a0)
- Nếu a > 0 thì min y = đạt tại hoành độ đỉnh xI =
- Nếu a < 0 thì y = đạt tại hoành độ đỉnh xI =
Trường hợp tập xác định khác R, ta kẻ bảng biến thiên của hàm số trên tập đó để có được giá trị lớn nhất, giá trị nhỏ nhất.
Bài tập:

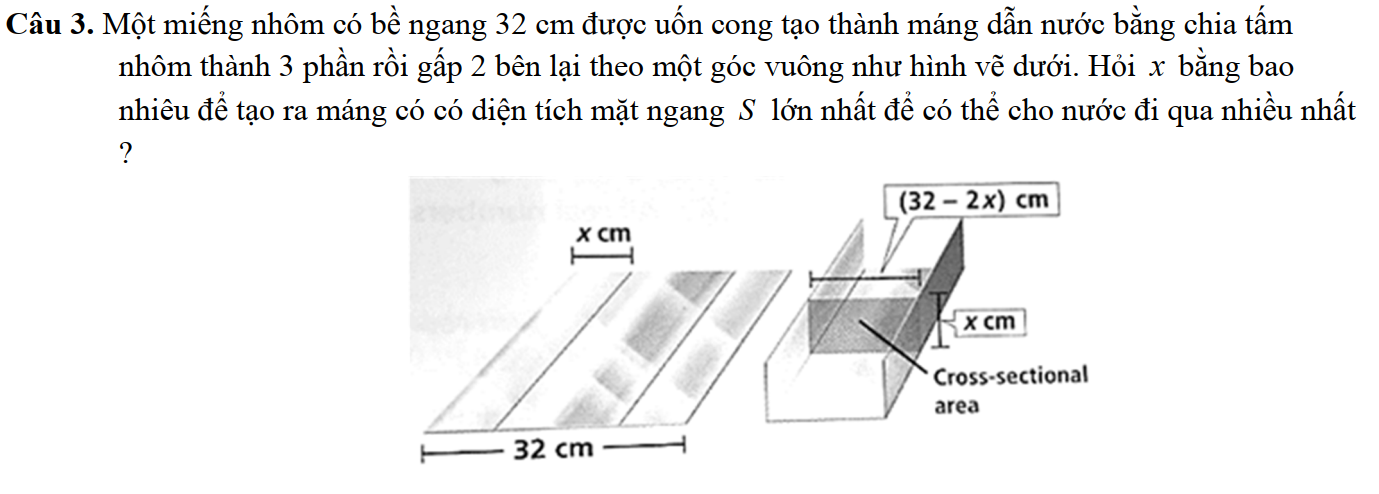
Vấn đề 7: Bài toán thực tế
Phương pháp:

Bài tập:

Hệ thống bài tập trắc nghiệm
Dạng 1. Sự biến thiên



Dạng 2. Xác định toạ độ đỉnh, trục đối xứng, hàm số bậc hai thỏa mãn điều kiện cho trước


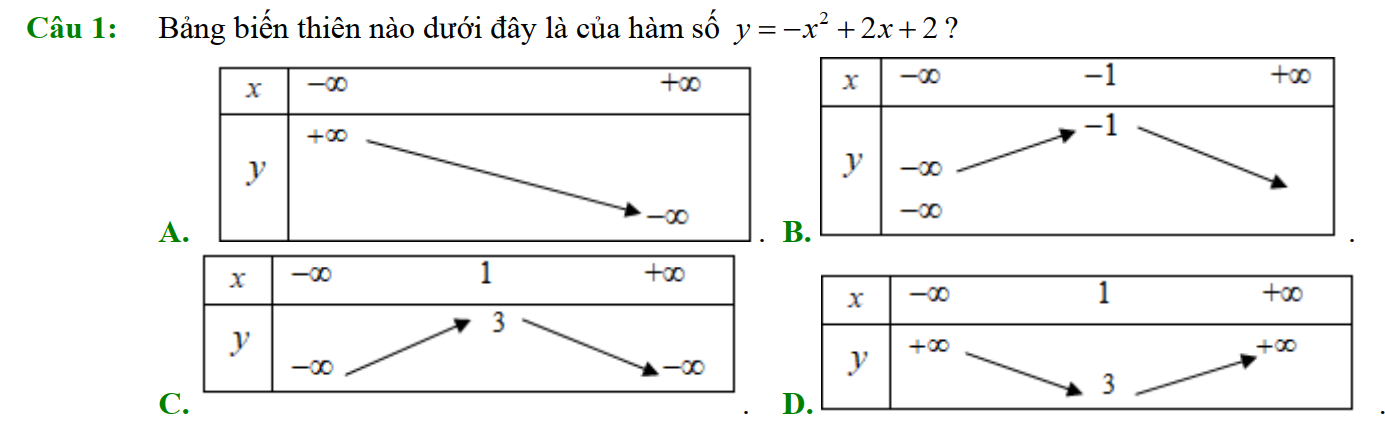
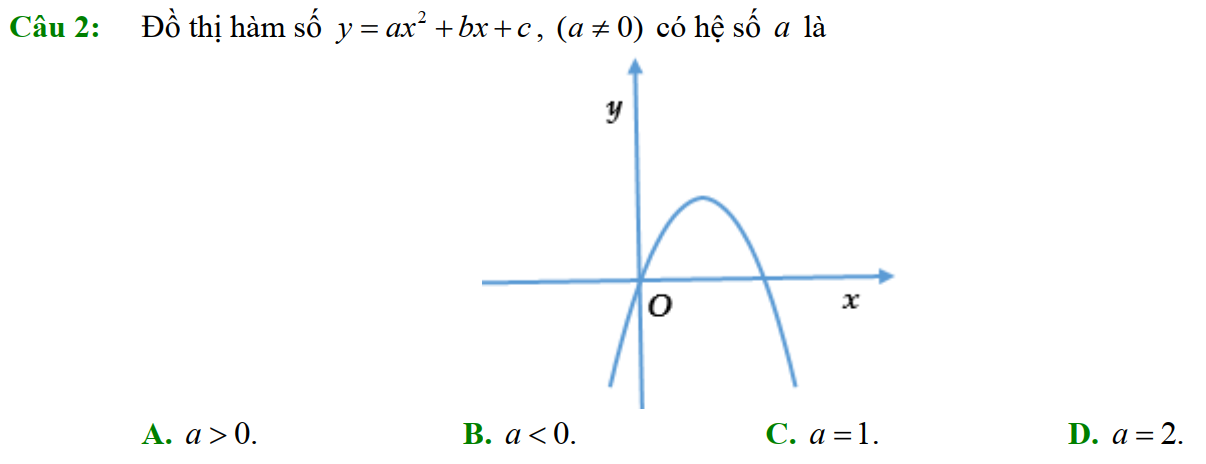
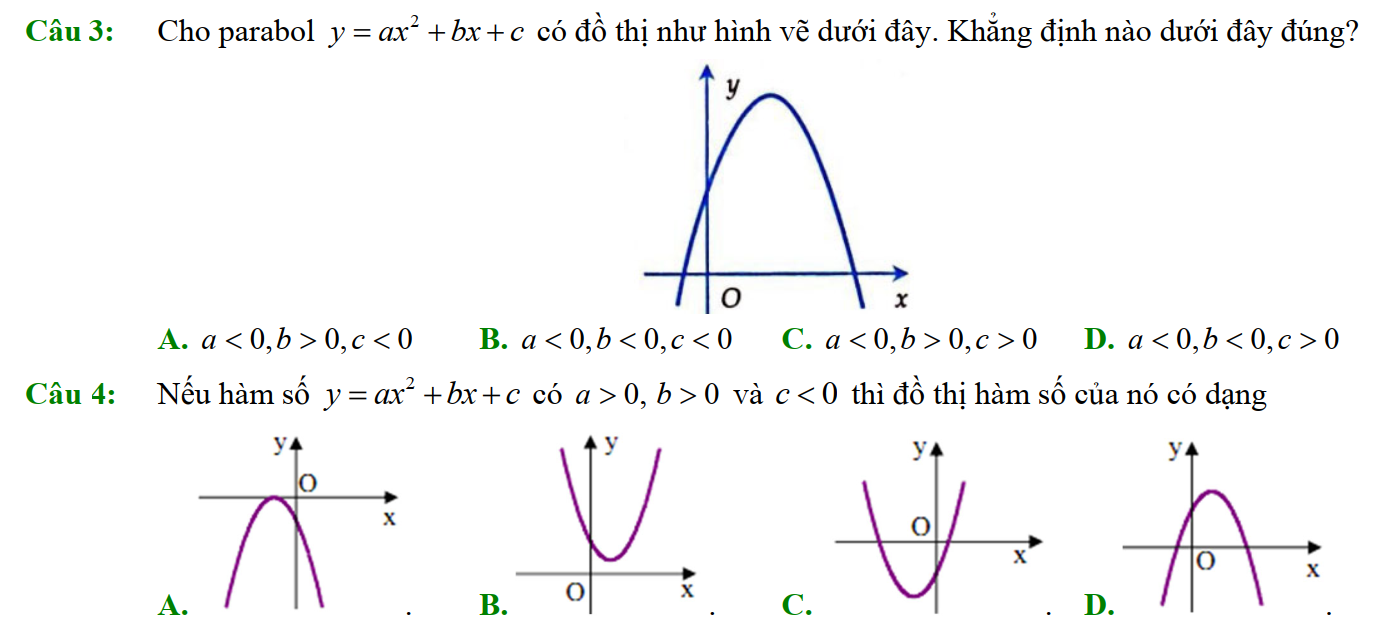
Dạng 3. Đọc đồ thị, bảng biến thiên của hàm số bậc hai
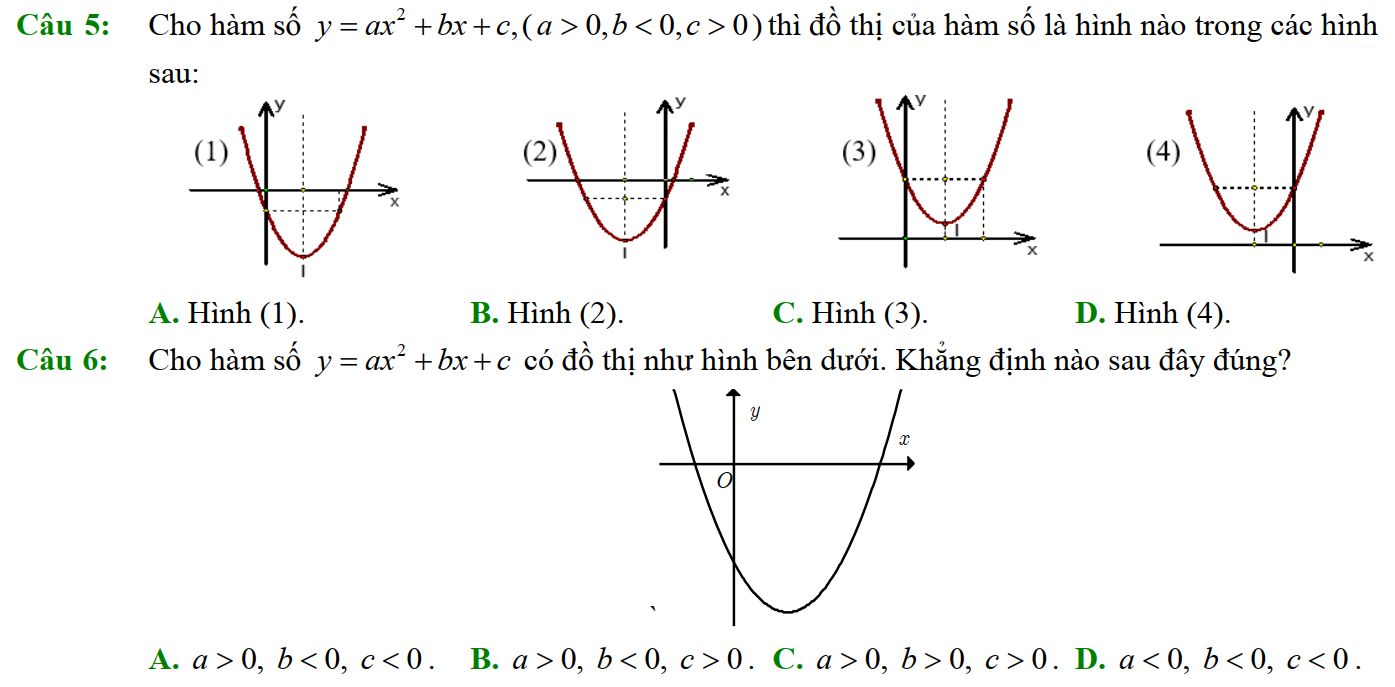
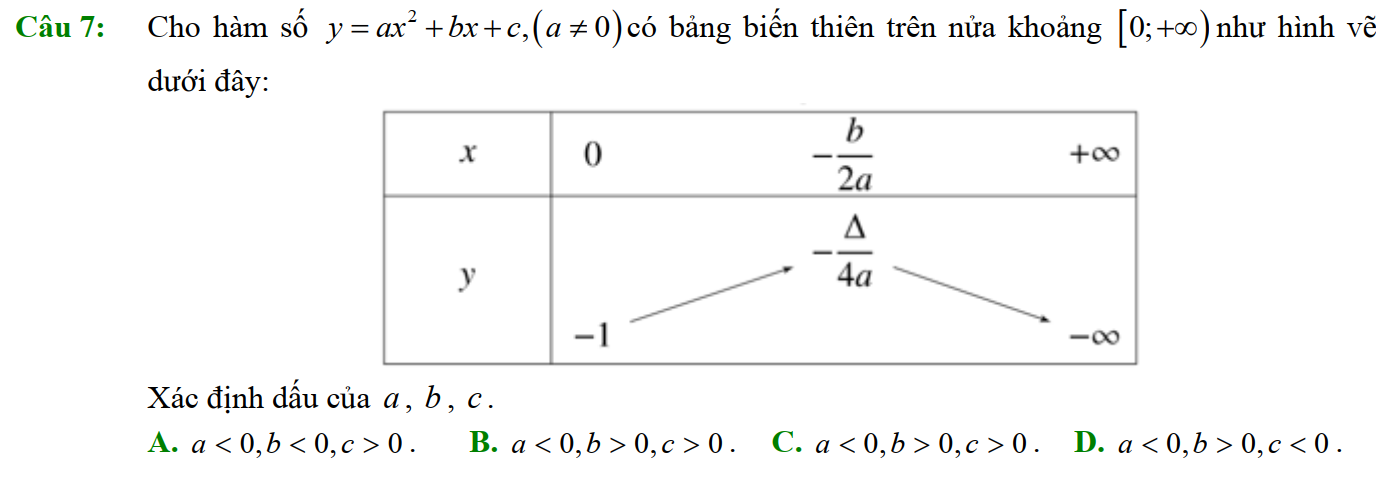
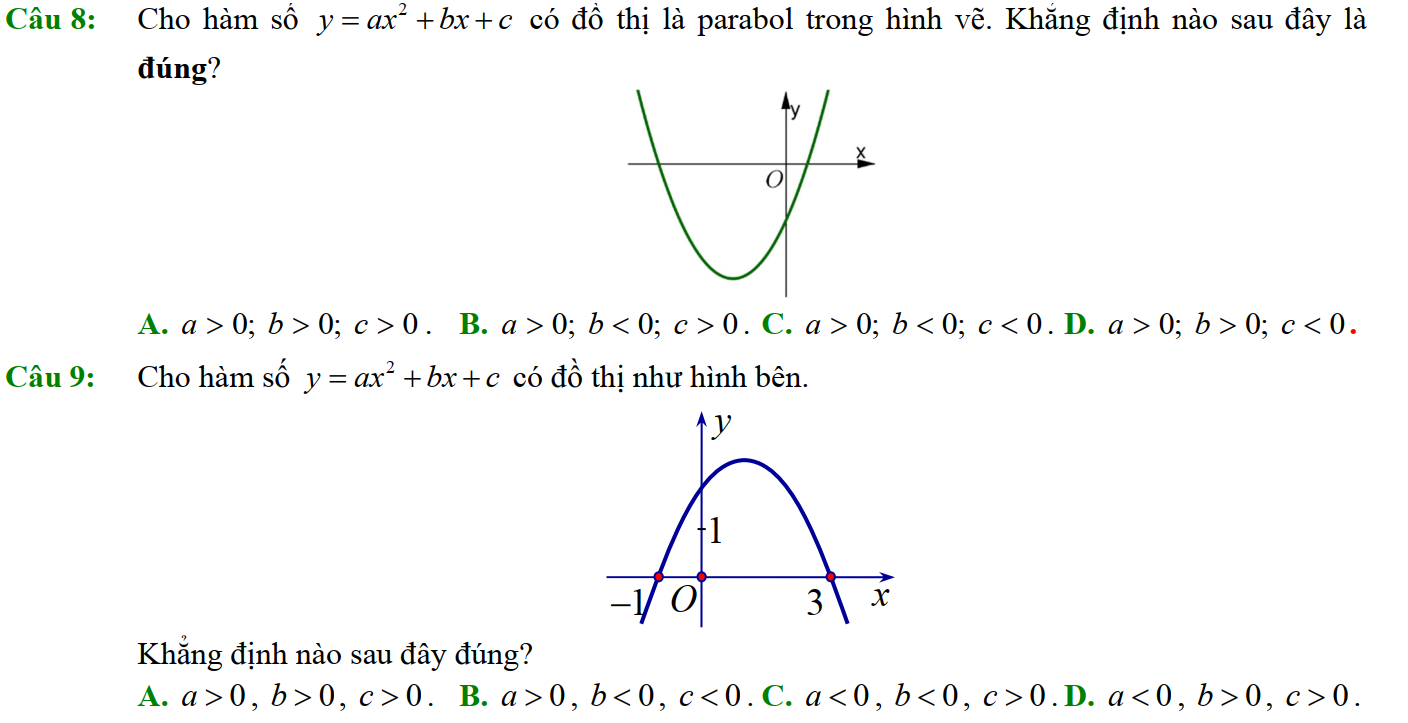
Dạng 4. Giá trị lớn nhất, giá trị nhỏ nhất
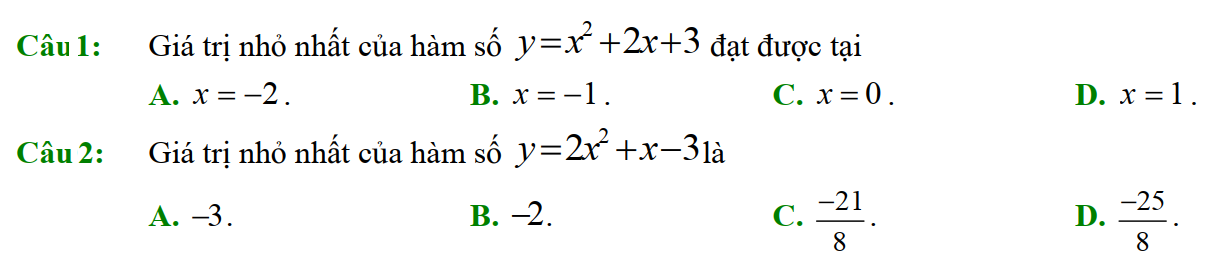


Dạng 5. Sự tương giao giữa parabol với đồ thị các hàm số

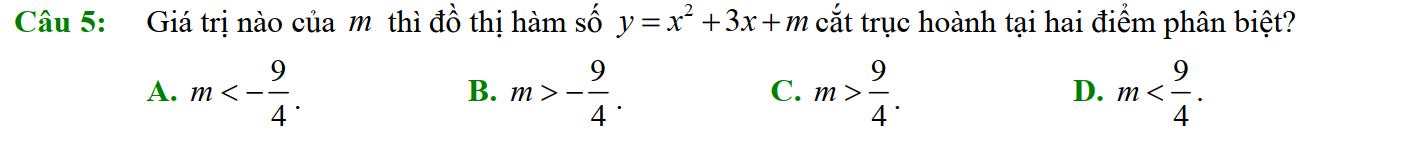

Dạng 6. Ứng dụng thực tế liên quan đến hàm số bậc hai


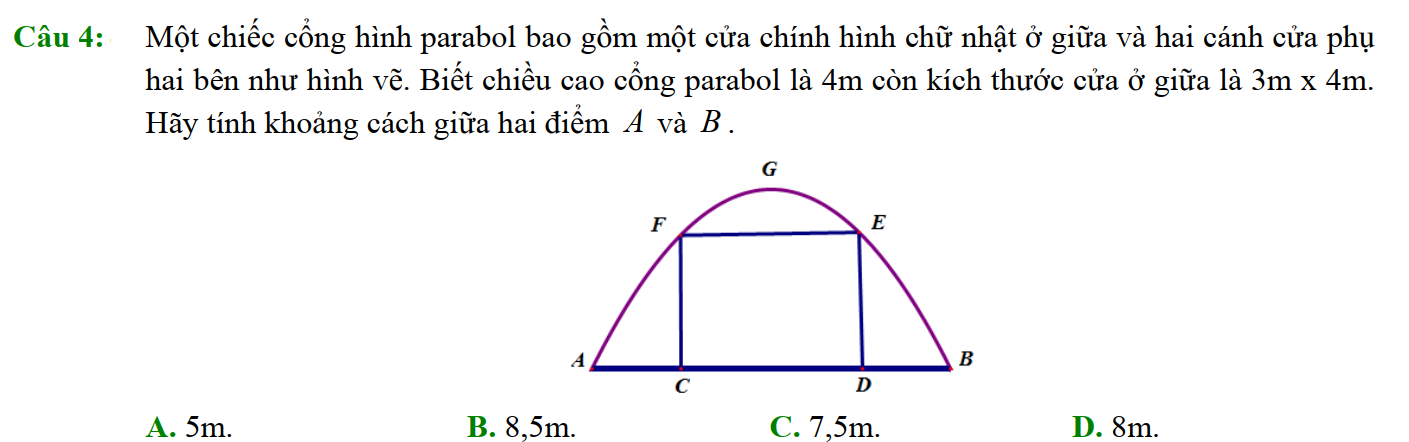
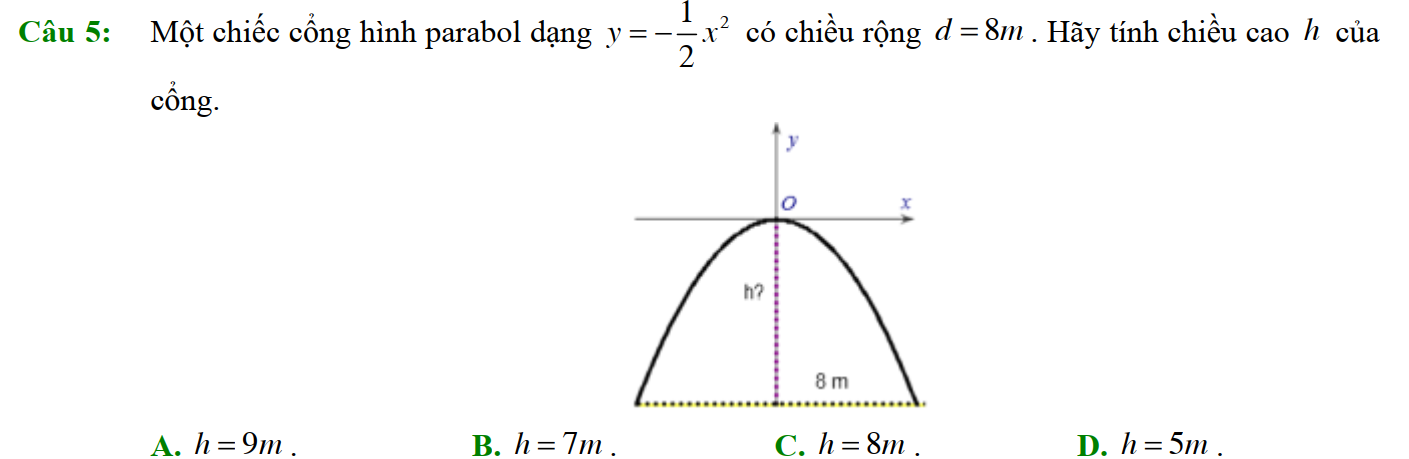
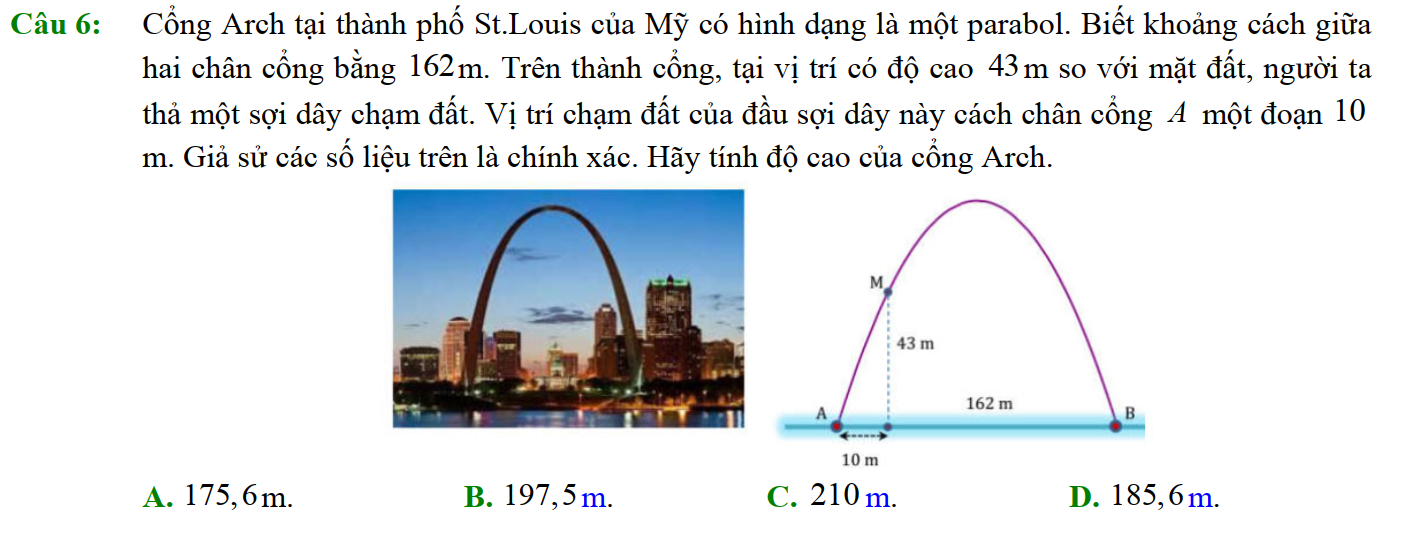


III. Dấu của tam thức bậc hai
Định lí:
Cho tam thức bậc hai có biệt thức .
- Nếu thì luôn cùng dấu với hệ số với mọi .
- Nếu thì có nghiệm kép .
Khi đó có cùng dấu với hệ số với mọi .
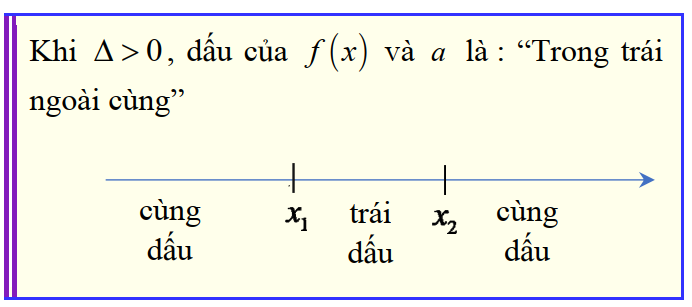
- Nếu có nghiệm và luôn cùng dấu với hệ số với mọi và luôn trái dấu với hệ số với mọi
Bài tập sách giáo khoa

Hệ thống bài tập tự luận
Dạng 1. Xét dấu biểu thức
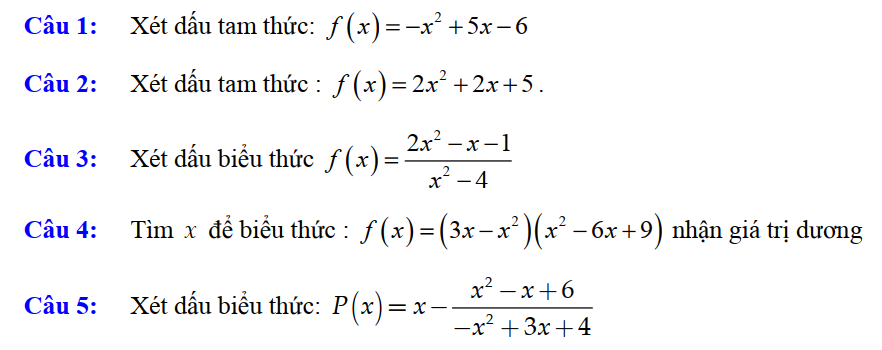
Dạng 2. Giải bất phương trình

Dạng 3. Giải hệ bất phương trình

Dạng 4. Điều kiện về dấu của tam thức bậc hai

Dạng 5. Điều kiện về nghiệm của tam thức bậc hai

Hệ thống bài tập trắc nghiệm
Dạng 1. Xét dấu tam thức bậc hai – bất phương trình bậc hai

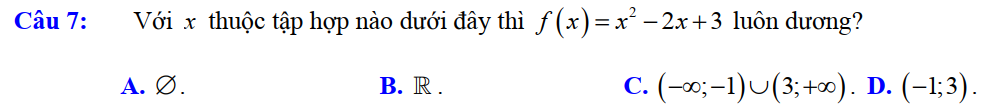

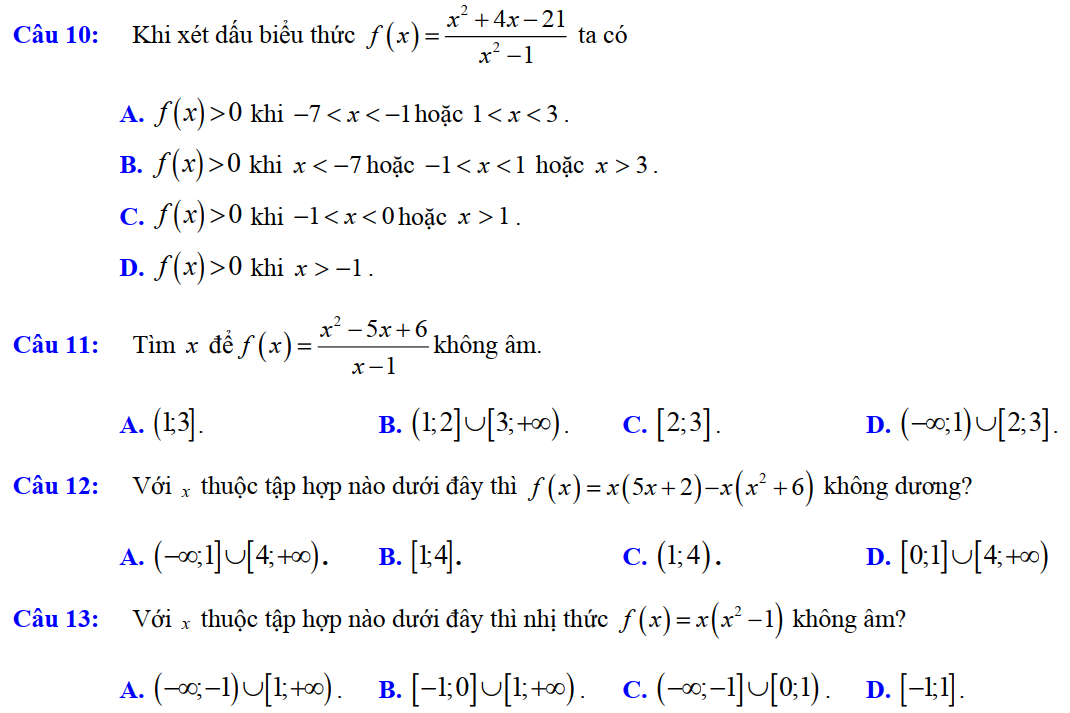

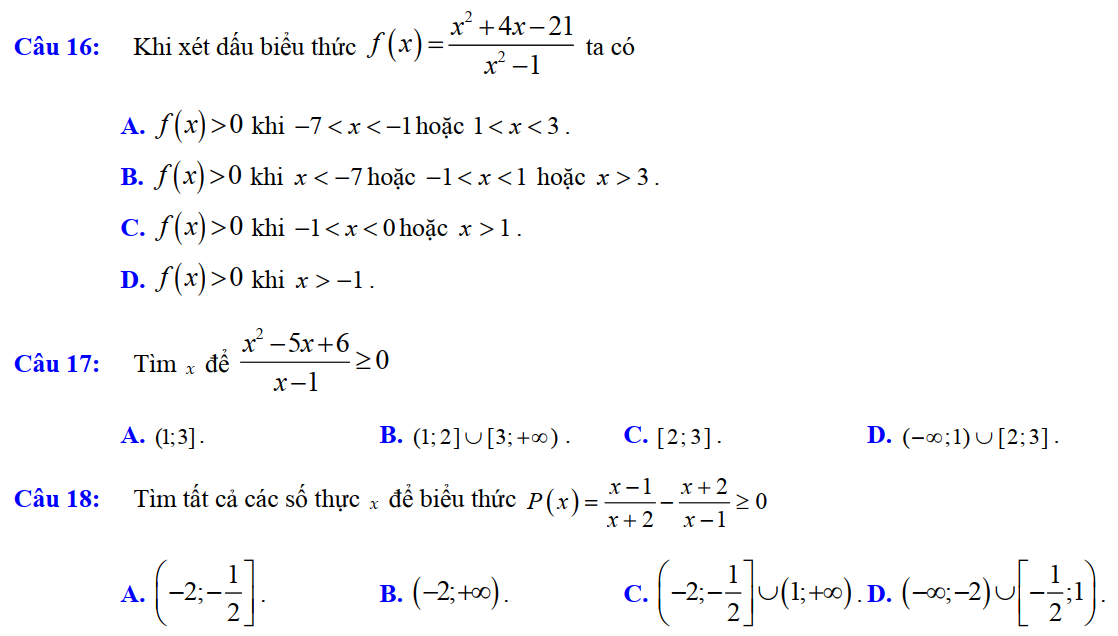

Dạng 2. Giải bất phương trình bậc hai và một số bài toán liên quan




Dạng 3. Bất phương trình tích



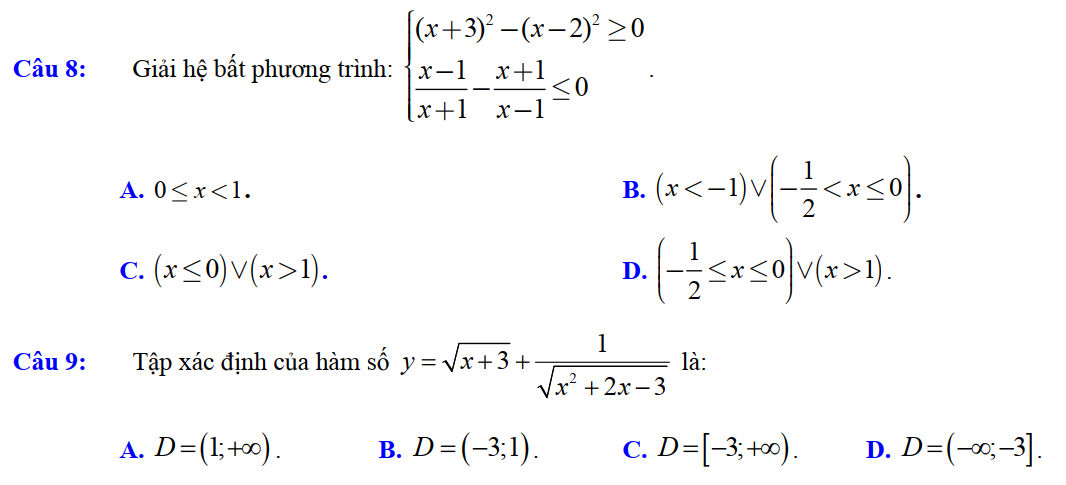
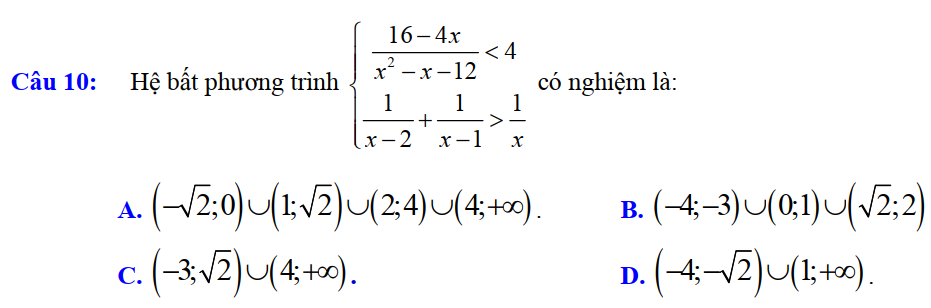
Dạng 4. Bất phương trình chứa ẩn ở mẫu


Dạng 5. Hệ bất phương trình bậc hai và các bài toán liên quan



Dạng 6. Bài toán chứa tham số
Dạng 6.1. Tìm m để phương trình có n nghiệm



Dạng 6.2. Tìm m để phương trình bậc 2 có nghiệm thỏa mãn điều kiện cho trước


Dạng 6.3. Tìm m để bất phương trình thỏa mãn điều kiện cho trước


Dạng 7. Tìm m để hệ bất phương trình bậc hai thỏa mãn điều kiện cho trước


Dạng 8. Bất phương trình chứa dấu giá trị tuyệt đối và một số bài toán liên quan

Dạng 9. Bất phương trình chứa căn và một số bài toán liên quan

IV. Phương trình quy về phương trình bậc hai
a. Phương trình trùng phương
+) Phương trình trùng phương là phương trình có dạng
+) Cách giải: Đặt ẩn phụ để đưa phương trình về phương trình bậc hai:
b. Phương trình chứa ẩn ở mẫu thức
Để giải phương trình chứa ẩn ở mẫu thức, ta có các bước giải như sau:
Bước 1. Tìm điều kiện xác định của ẩn của phương trình.
Bước 2. Quy đồng mẫu thức hai vế rồi khử mẫu.
Bước 3. Giải phương trình vừa nhận được ở bước 2.
Bước 4. So sánh các nghiệm tìm được ở bước 3 với điều kiện xác định và kết luận.
c. Phương trình đưa về dạng phương trình tích
Để giải phương trình đưa về dạng tích, ta có các bước giải như sau:
Bước 1. Phân tích vế trái thành nhân tử, vế phải bằng .
Bước 2. Xét từng nhân tử bằng để tìm nghiệm.
d) Sự tương giao giữa đường thẳng và parabol
Sự tương giao giữa đường thẳng và parabol
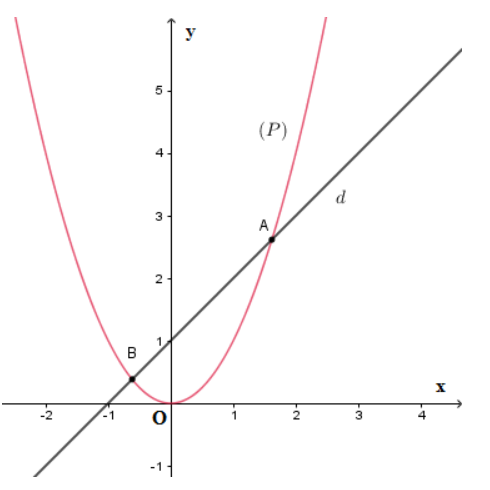
Số giao điểm của đường thẳng và parabol là số nghiệm của phương trình hoành độ giao điểm
(*)
+) Phương trình (*) có hai nghiệm phân biệt thì cắt tại hai điểm phân biệt
+) Phương trình (*) có nghiệm kép thì tiếp xúc với .
+) Phương trình (*) vô nghiệm thì không cắt
Bài tập sách giáo khoa

Hệ thống bài tập tự luận
V. Đồ thị hàm số
Đồ thị hàm số u = f(x) xác định trên tập D là tập hợp tất cả các điểm M(x; f(x)) trên mặt phẳng tọa độ với mọi x thuộc D. Hay có thể diễn tả bằng: M(x0; y0)(G) <=> y0 = f(x0) với x0D
VI. Bài tập vận dụng
Bài 1: Viết phương trình tiếp tuyến với đồ thị (C) của hàm số y = x3 - 3x2 + 1, biết tiếp tuyến đi qua điểm A(2;-3)
Lời giải:
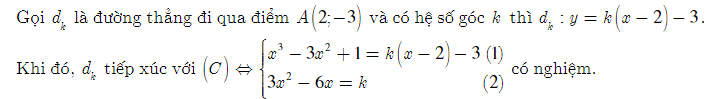
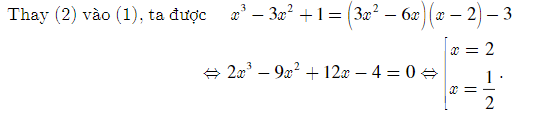
+) Với x = 2, thay vào (2) được k = 0, ta có tiếp tuyến dk: y = -3
+) Với x = , thay vào (2) được k = , ta có tiếp tuyến dk: y = x +
Bài 2: Tìm các giá trị của m để hàm số y = x3 + (2m - 1)x2 + (m + 1)x + 2m - 1
a. đồng biến trên
b. đồng biến trên [1;+)
Lời giải:
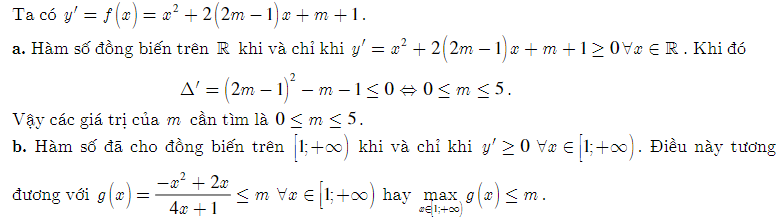
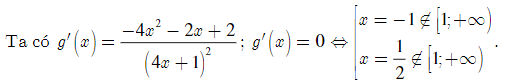
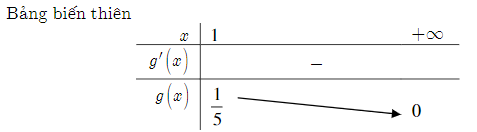
Ta thấy g(x) = g(1) = . Do đó ta có m . Vậy các giá trị m cần tìm là m .
Bài 3: Tìm các giá trị của m để hàm số y = x4 + (1 - m)x2 + 2m +1 có ba cực trị.
Lời giải:
Hàm số có ba cực trị
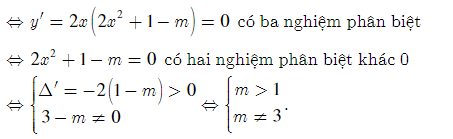
Bài 4: Tìm các giá trị của m để đồ thị hàm số y = x4 + mx2 + 6 - có ba điểm cực trị A, B, C (trong đó điểm A thuộc trục tung) sao cho tứ giác ABOC là hình bình hành.
Lời giải:
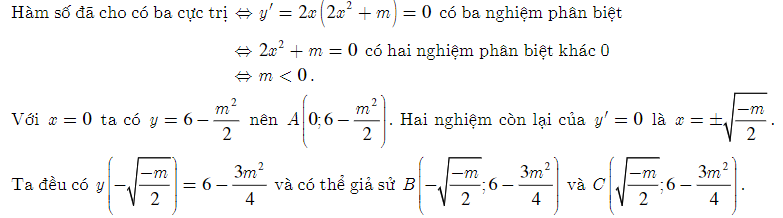
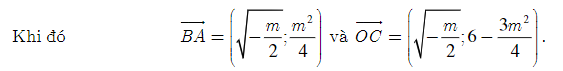
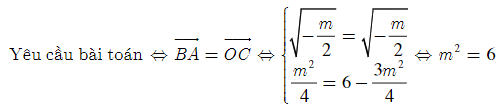
<=> m = (vì <=> m < 0)
Bài 5: Tìm các giá trị của m để đồ thị hàm số y = x3 + 3(m - 1)x2 + 3(m - 1)x + 1 có hai điểm cực trị, đồng thời đường thẳng nối hai điểm cực trị đi qua điểm A(0; -3)
Lời giải:

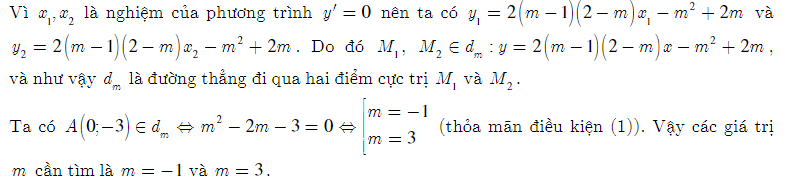
Bài 6: Tìm các giá trị của m để hàm số y = x3 + x2 + mx + m có cực đại và cực tiểu, đồng thời khoảng cách giữa hai điểm cực trị bằng
Lời giải:

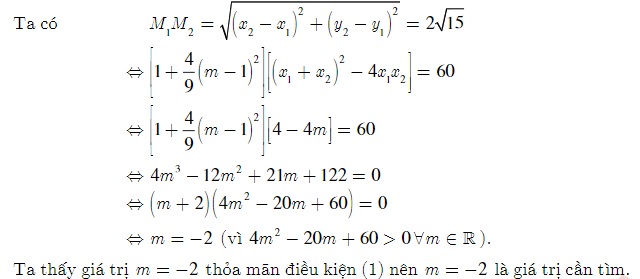
Bài 7: Cho hàm số y = (C). Viết phương trình tiếp tuyến của (C) biết tiếp tuyến đó cắt 2 trục tọa độ tại A, B sao cho tam giác OAB cân tại O.
Lời giải:
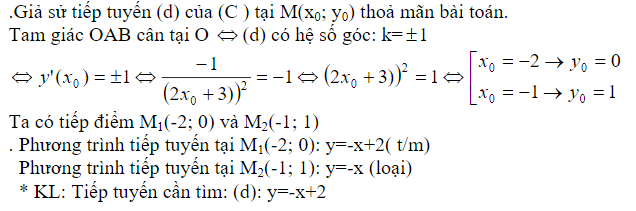
Xem các Phương pháp giải bài tập hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.