Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Bài tập phương trình nghiệm nguyên (HAY NHẤT 2024) gồm đầy đủ các phần ý thuyết, phương pháp giải, bài tập minh họa có lời giải chi tiết giúp học sinh nắm vững lý thuyết, biết cách giải các dạng Bài tập phương trình nghiệm nguyên từ đó có kế hoạch ôn tập hiệu quả để đạt kết quả cao trong các bài thi môn Toán.
Phương pháp giải Bài tập phương trình nghiệm nguyên (HAY NHẤT 2024)
A. Kiến thức cần nhớ
I. Giải phương trình nghiệm nguyên
Giải phương trình f(x,y,z,...) = 0 chứa các ẩn x, y, z,... với nghiệm nguyên là tìm tất cả các bộ số nguyên (x, y, z,...) thỏa mãn phương trình đó.
II. Một số lưu ý khi giải phương trình nghiệm nguyên
Khi giải các phương trình nghiệm nguyên cần vận dụng linh hoạt các tính chất về chia hết, đồng dư, tính chẵn lẻ … để tìm ra điểm đặc biệt của các ẩn số cũng như các biểu thức chứa ẩn trong phương trình, từ đó đưa phương trình về các dạng mà ta đã biết cách giải hoặc đưa về những phương trình đơn giản hơn. Các phương pháp thường dùng để giải phương trình nghiệm nguyên là: Phương pháp dùng tính chất chia hết; Phương pháp xét số dư từng vế; Phương pháp sử dụng bất đẳng thức; Phương pháp dùng tính chất của số chính phương; Phương pháp lùi vô hạn, nguyên tắc cực hạn.
B. Một số phương pháp giải phương trình nghiệm nguyên
I. Phương pháp dùng tính chia hết
Dạng 1: Phát hiện tính chia hết của một ẩn
Bài tập: Giải phương trình nghiệm nguyên 3x + 17y = 159 (1)
Lời giải:

Dạng 2: Phương pháp đưa về phương trình ước số
Phương pháp:
Ta tìm cách đưa phương trình đã cho thành phương trình có một vế là tích các biểu thức có giá trị nguyên, vế phải là hằng số nguyên.
Thực chất là biến đổi phương trình về dạng: A(x;y).B(x;y) = c trong đó A(x;y), B(x;y) là các biểu thức số nguyên, c là một số nguyên.
Xét các trường hợp A(x;y), B(x;y) theo ước của c.
Bài tập: Tìm nghiệm nguyên của phương trình: 5x - 3y = 2xy - 11
Lời giải:

Dạng 3: Phương pháp tách ra các giá trị nguyên
Phương pháp:
Trong nhiều bài toán phương trình nghiệm nguyên ta tách phương trình ban đầu thành các phần có giá trị nguyên để dễ dàng đánh giá tìm ra nghiệm, đa số các bài toán sử dụng phương pháp này thường rút một ẩn (có bậc nhất) theo ẩn còn lại.
Bài tập: Tìm nghiệm nguyên dương của phương trình sau: xy - 2y - 3y + 1 = 0
Lời giải:
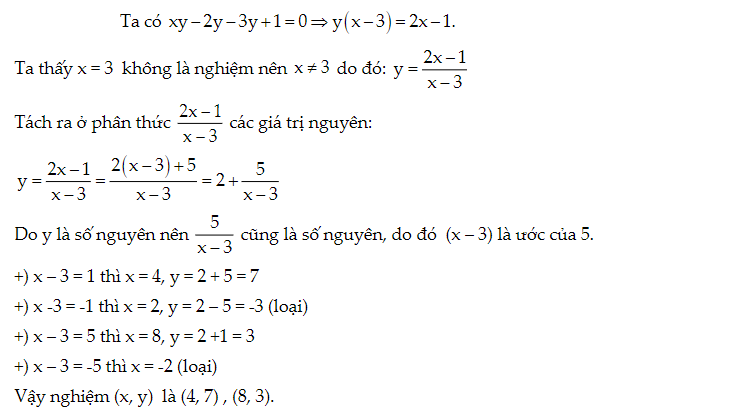
II. Phương pháp sử dụng tính chẵn lẻ của ẩn hoặc xét số dư từng vế
Dạng 1: Sử dụng tính chẵn lẻ
Phương pháp:
Dựa vào tính chẵn lẻ của ẩn hoặc xét số dư hai vế của phương trình nghiệm nguyên với một số nguyên nào đó rồi luận để giải bài toán.
Bài tập: Tìm x, y nguyên tố thỏa mãn y2 - 2x2 = 1
Lời giải:

Dạng 2: Xét tính chẵn lẻ và xét số dư từng vế
Bài tập: Tìm nghiệm nguyên của phương trình: 9x + 2 = y2 + y
Lời giải:

III. Phương pháp dùng bất đẳng thức
Dạng 1: Sử dụng bất đẳng thức cổ điển
Phương pháp:

Bài tập: Tìm các số nguyên dương x, y thỏa mãn phương trình: (x2 + 1)(x2 + y2) = 4x2y
Lời giải:
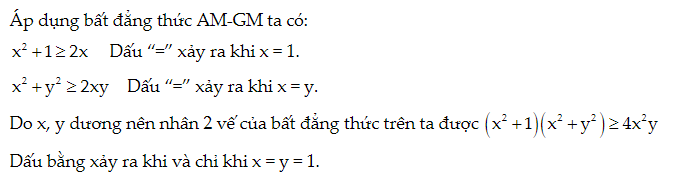
Dạng 2: Sắp xếp thứ tự các ẩn
Phương pháp:
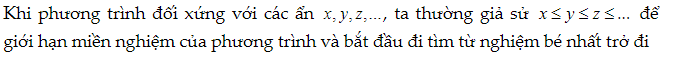
Bài tập: Giải phương trình nghiệm nguyên dương:
Lời giải:

Dạng 3: Chỉ ra nghiệm nguyên
Phương pháp:
Chúng ta xét từng khoảng giá trị của ẩn còn được thể hiện dưới dạng: chỉ ra một vài số là nghiệm của phương trình, rồi chứng minh phương trình không còn nghiệm nào khác.
Bài tập: Tìm nghiệm nguyên dương của phương trình sau: 3x + 4x = 5x
Lời giải:

Dạng 4: Sử dụng điều kiện ∆ ≥ 0 để phương trình bậc hai có nghiệm
Phương pháp:

Bài tập: Tìm nghiệm nguyên dương của phương trình sau: x2 + y2 - 2x + y = 9
Lời giải:

IV. Phương pháp dùng tính chất của số chính phương
Dạng 1: Dùng tính chất về chia hết của số chính phương
Phương pháp:

Bài tập: Tìm nghiệm nguyên của phương trình: 9x + 5 = y(y + 1)
Lời giải:

Dạng 2: Biến đổi phương trình về dạng trong đó là các đa thức hệ số nguyên là số nguyên dương, k là số tự nhiên
Phương pháp:

Bài tập: Tìm nghiệm nguyên của phương trình: x2 + y2 - x - y = 8
Lời giải:

Dạng 3: Xét các số chính phương liên tiếp
Phương pháp:
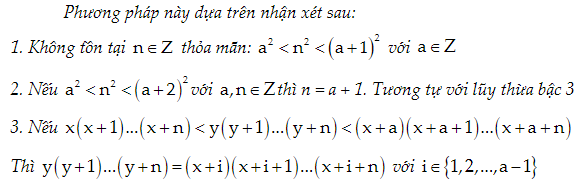
Bài tập: Tìm nghiệm nguyên của phương trình: 1 + x + x2 + x3 = y3 (1)
Lời giải:

Dạng 4: Sử dụng điều kiện ∆ là số chính phương
Phương pháp:

Bài tập: Giải phương trình có nghiệm nguyên: 3x2 + y2 + 4xy + 4x + 2y + 5 = 0
Lời giải:

Dạng 5: Sử dụng tính chất: Nếu hai số nguyên liên tiếp có tích là một số chính phương thì một trong hai số nguyên liên tiếp đó bằng 0
Phương pháp:
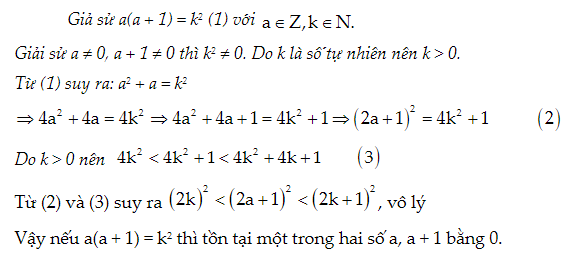
Bài tập: Tìm nghiệm nguyên của phương trình: x2 + 2xy = 5y + 6 (1)
Lời giải:

Dạng 6: Sử dụng tính chất: Nếu hai số nguyên dương nguyên tố cùng nhau có tích là một số chính phương thì mỗi số đều là số chính phương
Phương pháp:

Bài tập: Tìm nghiệm nguyên dương của phương trình: xy = z2
Lời giải:

V. Phương pháp lùi vô hạn, nguyên tắc cực hạn
Dạng 1: Phương pháp lùi vô hạn
Phương pháp:

Bài tập: Giải phương trình nghiệm nguyên sau: x2 + y2 = 3z2
Lời giải:

Dạng 2: Nguyên tắc cực hạn
Phương pháp:

Bài tập: Giải phương trình nghiệm nguyên sau: 8x4 + 4y4 + 2y4 = t4 (1)
Lời giải:

C. Bài tập vận dụng
Bài 1. Tìm số nguyên x, y, z thỏa mãn đồng thời: x2 + 4y2 + z2 + 2xz + 4(x + z) = 396 và x2 + y2 = 3z.
Lời giải

Bài 2. Tìm tất cả các cặp số nguyên (x;y) thỏa mãn 2x2 + 5y2 = 41 + 2xy
Lời giải
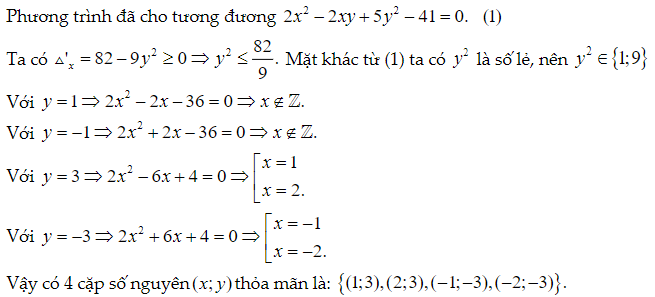
Bài 3. Tìm nghiệm nguyên của phương trình: 3x2 - 2xy + y - 5x + 2 = 0
Lời giải

Bài 4. Tìm tất cả các cặp số nguyên (x;y) thỏa mãn
Lời giải
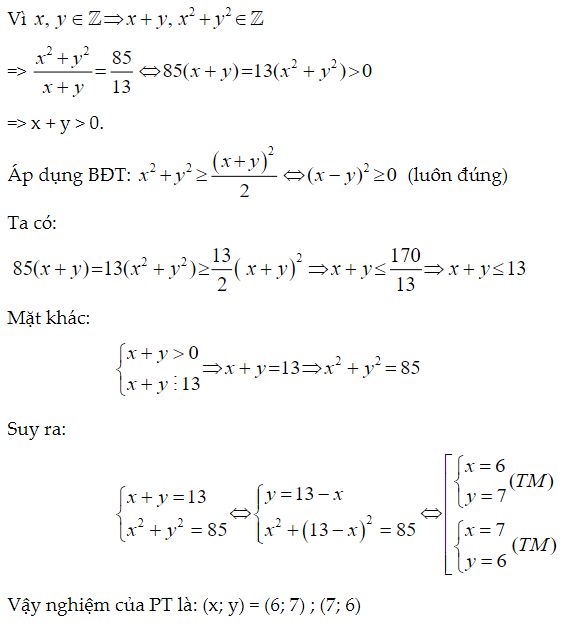
Bài 5. Tìm x, y thỏa mãn:
Lời giải
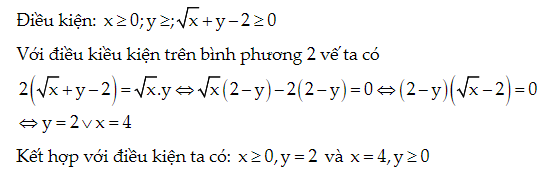
Bài 6. Tìm tất cả các nghiệm nguyên dương của phương trình: xy2 + 2xy - 243y + x = 0
Lời giải

Bài 7. Tìm các số nguyên không âm a, b, n thỏa mãn:
Lời giải
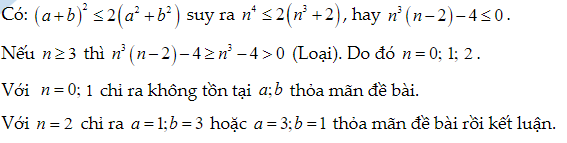
Bài 8. Tìm nghiệm nguyên của phương trình: y2 - 5y + 62 = (y - 2)x2 + (y2 - 6y +8)x
Lời giải
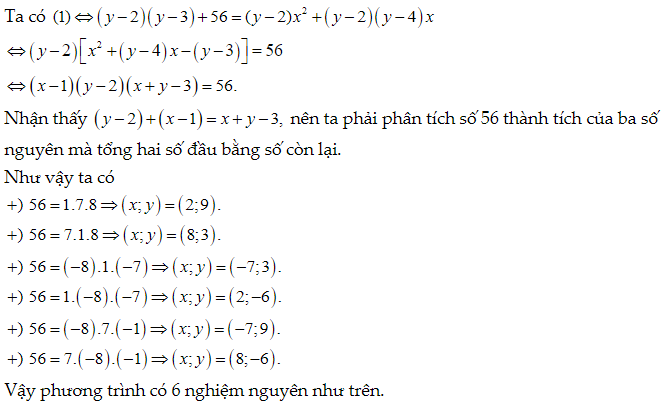
Bài 9. Tìm tất cả các cặp số nguyên (x;y) thỏa mãn: x(x2 + x + 1) = 4y - 1
Lời giải

Bài 10. Tìm các số nguyên x, y thỏa mãn: 4x = 1 + 3y
Lời giải
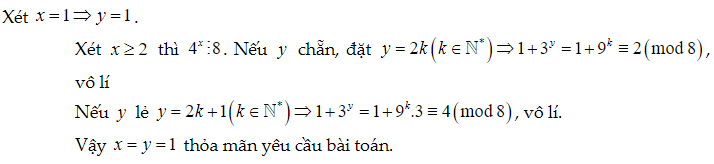
Xem các Phương pháp giải bài tập hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.