Lưu ý:

+ Nếu có  đối tượng khác nhau xếp vào  vị trí thì có:  cách sắp xếp.

+ Nếu  đối tượng giống nhau xếp vào  vị trí thì có:  cách sắp xếp.

+ Một số bài toán chứa điều kiện thì có thể chia nhỏ thành các trường hợp để khi sắp xếp không bị lặp lại.

II. Bài tập vận dụng

Bài 1: Có bao nhiêu cách sắp xếp năm bạn học sinh A, B, C, D, E vào một chiếc ghế dài sao cho:

1. Bạn C ngồi chính giữa.

2. Hai bạn A và E ngồi ở hai đầu ghế.

Lời giải:

1. Xếp C ngồi chính giữa có một cách xếp.

Xếp 4 học sinh A, B, D, E vào 4 vị trí còn lại có  cách xếp.

Vậy có:  cách xếp.

2. Xếp A và E ngồi ở hai đầu ghế có  cách xếp là A ngồi đầu này, E ngồi đầu kia của ghế và ngược lại.

Xếp 3 học sinh B, C, D vào 3 vị trí còn lại có  cách xếp có  cách xếp.

Bài 2: Một nhóm gồm 10 học sinh, trong đó có 7 nam và 3 nữ. Hỏi có bao nhiêu cách sắp xếp 10 học sinh trên thành một hàng dài sao cho 7 học sinh nam phải đứng liền nhau.

Lời giải:

Coi 7 học sinh nam đứng liền nhau như một vị trí, đặt a là vị trí của 7 học sinh nam thì số cách để bố trí a đứng liền nhau xen kẽ với 3 học sinh nữ bằng  Nhưng để xếp 7 học sinh nam đứng liền nhau thì lại có  cách.

Vậy tất cả có:  cách.

Bài 3: Có 12 đội bóng tham gia tranh giải vô địch quốc gia. Trong vòng đấu loại các đối thủ đấu với nhau theo thể thức vòng tròn, hai đội bóng bất kỳ gặp nhau hai trận, một trận lượt đi và một trận lượt về. Hỏi có bao nhiêu trận đấu trong vòng loại?

Lời giải:

Mỗi đội bóng bất kỳ thì 11 trận đấu với 11 đội bóng còn lại.

Suy ra số trận đấu là:  trận.

Bài 4: Có bao nhiêu cách chọn 4 cầu thủ khác nhau trong 10 cầu thủ của đội bóng quần vợt để chơi bốn trận đấu đơn, các trận đấu là có thứ tự?

Lời giải

Mỗi cách chọn bốn cầu thủ của đội bóng là một chỉnh hợp chập 4 của 10 phần tử.

Ta có:  cách chọn.

Bài 5. Có bao nhiêu cách sắp xếp chỗ ngồi cho 10 bạn trong đó có An và Bình vào 10 ghế kê thành hàng ngang sao cho 

a) Hai bạn An và Bình ngồi cạnh nhau

b) Hai bạn An và Bình không ngồi cạnh nhau

Lời giải

a) Hai bạn An và Bình ngồi cạnh nhau

Ghép 2 bạn An và Bình ngồi gần nhau: Số cách sắp xếp của 2 bạn 2!

An, Bình và 8 bạn còn lại được tính là 9 phần tử: 9!

Số cách thực hiện là: 2!.9!

b) Hai bạn An và Bình không ngồi cạnh nhau

Sắp xếp chỗ ngồi cho 10 bạn bất kì là: 10!

Số cách sắp xếp chỗ  để An và Bình không ngồi cạnh nhau là : 10! – 9!.2! = 8.9!

Bài 6. Một học sinh có  cuốn sách đôi một khác nhau, trong đó có  cuốn sách Toán,  cuốn sách Văn và  cuốn sách Anh. Hỏi có bao nhiêu cách xếp tất cả các cuốn sách lên một kệ sách dài, nếu các cuốn sách cùng môn được xếp kề nhau?

Lời giải:

Có  cách xếp  nhóm sách (nhóm sách Toán, nhóm sách Văn, nhóm sách Anh) lên một kệ dài.

Mỗi cách xếp đó có  cách xếp  cuốn sách toán,  cách xếp  cuốn sách Văn và  cách xếp cuốn sách Anh.

Vậy theo quy tắc nhân có:  cách xếp tất cả các cuốn sách lên một kệ sách dài, và các cuốn sách cùng môn được xếp kề nhau.

Bài 7. Một bàn dài có hai dãy ghế đối diện nhau, mỗi dãy có  ghế. Người ta muốn xếp chỗ ngồi cho  học sinh trường A và  học sinh trường B vào bàn nói trên. Hỏi có bao nhiêu cách xếp trong mỗi trường hợp sau:

1. Bất cứ  học sinh nào ngồi cạnh nhau hoặc đối diện nhau thì khác trường với nhau.

2. Bất cứ  học sinh nào ngồi đối diện nhau thì khác trường với nhau.

Lời giải:

1) Có hai sơ đồ xếp chỗ ngồi sao cho cứ  học sinh nào ngồi cạnh nhau hoặc đối diện nhau thì khác trường với nhau là:

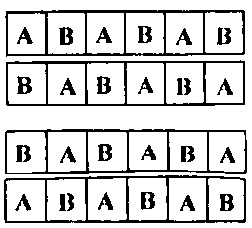
Mỗi sơ đồ có  cách sắp xếp  học sinh trường A và  cách sắp xếp  học sinh trường B.

Vậy theo quy tắc nhân có:  cách sắp xếp.

2) Học sinh thứ nhất trường A ngồi trước: có  cách chọn ghế để ngồi.

Sau đó, chọn học sinh trường B ngồi đối diện với học sinh thứ nhất trường A: có  cách chọn học sinh trường B.

Học sinh thứ hai của trường A còn  chỗ để chọn, chọn học sinh trường B ngồi đối diện với học sinh thứ hai trường A: có  cách chọn ..v.v..

Vậy có   cách.

Bài 8. Có  thẻ trắng và  thẻ đen, đánh dấu mỗi loại theo các số , , , ,  Có bao nhiêu cách sắp xếp tất cả các thẻ này thành một hàng sao cho hai thẻ cùng màu không nằm liền nhau.

Lời giải:
Có  trường hợp xảy ra:

Trường hợp 1: Các thẻ trắng ở vị trí lẻ, các thẻ đen ở vị trí chẵn.

Có  cách sắp xếp  thẻ trắng và  cách sắp xếp  thẻ đen.

Suy ra có:  cách sắp xếp.

Trường hợp 2: Các thẻ trắng ở vị trí chẵn, các thẻ đen ở vị trí lẻ.

Có  cách sắp xếp  thẻ trắng và  cách sắp xếp  thẻ đen.

Suy ra có  cách sắp xếp.

Vậy có:  cách sắp xếp.

Bài 9. Một thầy giáo có  cuốn sách đôi một khác nhau trong đó có  cuốn sách Văn,  cuốn sách Nhạc và  cuốn sách Họa. Ông muốn lấy ra  cuốn và tặng cho  học sinh A, B, C, D, E, F mỗi em một cuốn.

1. Giả sử thầy giáo chỉ muốn tặng cho các học sinh trên những cuốn sách thuộc  thể loại Văn và Nhạc. Hỏi có bao nhiêu cách tặng?

2. Giả sử thầy giáo muốn rằng sau khi tặng sách xong, mỗi một trong ba loại sách trên đều còn lại ít nhất một cuốn. Hỏi có bao nhiêu cách chọn?

Lời giải:

1. Số cách tặng là số cách chọn  cuốn sách từ  cuốn có kể thứ tự, tức là mỗi cách chọn là một chỉnh hợp chập  của 

Vậy số cách tặng là 

2. Nhận xét: không thể chọn sao cho cùng hết  loại sách.

Số cách chọn  cuốn sách từ  cuốn sách là: 

Số cách chọn sao cho không còn sách Văn là: 

Số cách chọn sao cho không còn sách Nhạc là: 

Số cách chọn sao cho không còn sách Hoạ là: 

Số cách chọn cần tìm là: 

Bài 10. Có  nam và  nữ ngồi vào hai dãy ghế đối diện nhau, mỗi dãy có  ghế. Hỏi:

a) Có bao nhiêu cách sắp xếp sao cho hai người đối diện khác phái?

b) Có bao nhiêu cách sắp xếp mà nam nữ ngồi xen kẽ và đối diện?

Lời giải:
a) Học sinh nam thứ nhất có  cách chọn chỗ ngồi, sau đó chọn  học sinh nữ ngồi đối diện với học sinh nam đã chọn có  cách.

Học sinh nam thứ hai có  cách chọn chỗ ngồi, chọn  học sinh nữ ngồi đối diện có  cách.

Học sinh nam thứ ba có  cách chọn chỗ ngồi, chọn  học sinh nữ ngồi đối diện có  cách.

Học sinh nam thứ tư có  cách chọn chỗ ngồi, chọn  học sinh nữ ngồi đối diện có  cách.

Học sinh nam thứ hai có  cách chọn chỗ ngồi, chọn  học sinh nữ ngồi đối diện có  cách.

Vậy có  cách sắp xếp để hai người đối diện khác phái.

Cách khác:

Chọn cặp nam, nữ thứ nhất và xếp vào  ghế đối diện đã chọn có  cách chọn (có thể nam_nữ hoặc nữ_nam).

Chọn cặp nam, nữ thứ hai và xếp vào  ghế đối diện đã chọn có  cách chọn (có thể nam_nữ hoặc nữ_nam).

Chọn cặp nam, nữ thứ ba và xếp vào  ghế đối diện đã chọn có  cách chọn (có thể nam_nữ hoặc nữ_nam).

Chọn cặp nam, nữ thứ tư và xếp vào  ghế đối diện đã chọn có  cách chọn (có thể nam_nữ hoặc nữ_nam).

Chọn cặp nam, nữ thứ năm và xếp vào  ghế đối diện đã chọn có  cách chọn (có thể nam_nữ hoặc nữ_nam).

Vậy có  cách.

b) Có  sơ đồ để sắp xếp nam nữ đối diện và xen kẽ là: (ký hiệu B: nam và G: nữ).

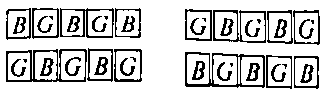
Mỗi sơ đồ có  cách sắp xếp  nam và  cách sắp xếp  nữ.

Vậy có  cách sắp xếp nam nữ ngồi xen kẽ và đối diện.

Bài 11: Cần xếp  nam và  nữ vào  hàng ghế có  chỗ ngồi sao cho  nam ngồi kề nhau và  nữ ngồi kề nhau. Hỏi có bao nhiêu cách.

Lời giải:

Giả sử ghế có  chỗ ngồi như sau: ▯▯▯▯▯▯▯.

Đầu tiên ta coi  nam là một khối thống nhất là a và  nữ là một khối thống nhất là b và c là 2 ghế trống còn lại.

+ Hoán vị  khối a, b và c có  cách.

+ Có  cách sắp xếp  nam của khối a và  cách xếp  nữ của khối b

+ c gồm  ghế không phân biệt nên chỉ có  cách.

Vậy có  cách sắp xếp.

Bài 12: Có bao nhiêu cách chọn  cầu thủ khác nhau trong  cầu thủ của đội bóng quần vợt để chơi bốn trận đấu đơn, các trận đấu là có thứ tự?

Lời giải:

Mỗi cách chọn bốn cầu thủ của đội bóng là một chỉnh hợp chập  của  phần tử.

Ta có:  cách chọn.

Bài 12: Người ta xếp ngẫu nhiên  lá phiếu từ  đến  cạnh nhau.

a) Có bao nhiêu cách sắp xếp để các phiếu số chẵn luôn ở cạnh nhau .

b) Có bao nhiêu cách xếp để các phiếu phân thành các nhóm chẵn lẻ riêng biệt.

Lời giải:

Giả sử  lá phiếu chẵn đứng cạnh nhau là một khối thống nhất A

Xếp khối A và  lá phiếu còn lại có  cách xếp.

Xếp  lá phiếu trong khối A có  cách xếp.

Vậy có  cách xếp.

b) Có  trường hợp để xếp  lá phiếu thành hai nhóm riêng biệt đó là các phiếu chẵn ở bên trái và

các phiếu lẻ ở phía bên phải và ngược lại.

Mỗi trường hợp có  cách xếp  phiếu lẻ và  cách xếp  phiếu chẵn.

Vậy có  cách xếp.

Bài 13: Một tổ gồm  nam và  nữ. Có bao nhiêu cách xếp hàng sao cho các bạn nữ đứng thành  2 cặp và  cặp này không đứng cạnh nhau?

Lời giải:

Chọn nhóm A gồm  nữ là  cách chọn.

 nữ còn lại là nhóm B có  cách chọn.

Suy ra có  cách chia  nữ thành  nhóm A và B (mỗi nhóm  nữ).

Mỗi cách chia trên có  cách xếp nhóm A, B và  bạn nam. Và có  cách xếp  nữ trong nhóm A,  cách xếp  nữ trong nhóm B.

Vậy có  cách sắp xếp  nam và  nữ theo một hàng sao cho nữ đứng thành 2 cặp.

Mặt khác khi hoán đổi vị trí cho nhau thì số nữ sẽ được tính lặp lại  lần do đó số cách sắp xếp là:
 cách.

Trong các cách trên ta xét trường hợp  nữ đứng cạnh nhau.

Gọi C là khối thống nhất của  nữ đứng cạnh nhau.

Có  cách xếp C và  bạn nam.

Mỗi cách xếp như trên có  cách xếp  bạn nữ trong khối C.

Suy ra có:  cách xếp để  nữ đứng cạnh nhau.

Vậy có  cách xếp thỏa mãn yêu cầu bài toán.

Cách khác:

Giả sử xếp  nam và  nữ thành hàng theo số thứ tự:

Ta tính số trường hợp xảy ra như sau:

+ Nếu  nữ xếp vào vị trí  thì  nữ còn lại có  cách chọn vị trí (; ; ; ; ; ; ).

+ Nếu  nữ xếp vào vị trí  thì  nữ còn lại có  cách xếp vào  vị trí liền nhau mà không trùng với trường hợp trên.

+ Nếu  nữ xếp vào vị trí  thì  nữ còn lại có  cách xếp vào  vị trí liền nhau mà không trùng  trường hợp trên.
… … …

+ Nếu  nữ xếp vào vị trí  thì  nữ còn lại có  cách xếp vào vị trí 
Suy ra có tất cả  trường hợp để nữ xếp thành  cặp và  cặp này không đứng cạnh nhau.

Mỗi trường hợp có  cách xếp  nữ và  cách xếp  nam.

Vậy có  cách xếp thỏa mãn yêu cầu bài toán.

Xem các Phương pháp giải bài tập hay, chi tiết khác: 

• Phương pháp giải Bài tập phương trình nghiệm nguyên (HAY NHẤT 2024)
• Phương pháp giải Bài tập tính khoảng cách trong hình học không gian (HAY NHẤT 2024)
• Phương pháp Áp dụng bất đẳng thức Cô - si, tìm GTLN - GTNN của biểu thức (HAY NHẤT 2024)
• Phương pháp giải Bài tập về điều kiện để hai đường thẳng tiếp xúc (HAY NHẤT 2024)
• Phương pháp giải Bài tập về hàm số, đồ thị và các vấn đề liên quan (HAY NHẤT 2024)