Toptailieu biên soạn và giới thiệu giải Sách bài tập Toán 8 Bài 14: Hình thoi và hình vuông sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập trong SBT Toán 8 Bài 14.

SBT Toán 8 (Kết nối tri thức) Bài 14: Hình thoi và hình vuông

Bài 3.23 trang 42 sách bài tập Toán 8 Tập 1: Chứng minh hình bình hành có hai đường cao xuất phát từ một đỉnh bằng nhau là một hình thoi.

Lời giải:

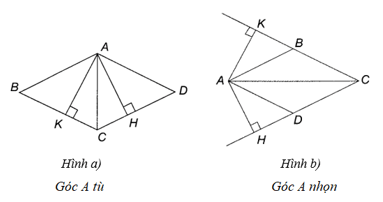
Xét hình bình hành ABCD có đường cao AH (H thuộc đường thẳng CD), và đường cao AK (K thuộc đường thẳng BC), AH = AK.

Xét DACH vuông tại H và DACK vuông tại K có:

Cạnh AC chung, AH = AK

Do đó ∆ACH = ∆ACK (cạnh huyền – một cạnh góc vuông)

Suy ra $\widehat{ACK}=\widehat{ACH}$(hai góc tương ứng)

Nên CA là tia phân giác của $\widehat{C}$.

Hình bình hành ABCD có CA là phân giác $\widehat{C}$ nên là hình thoi.

Bài 3.24 trang 42 sách bài tập Toán 8 Tập 1: Gọi O là giao điểm hai đường chéo của hình bình hành ABCD. Với mỗi tam giác OAB, OBC, OCD, ODA, xét giao điểm ba đường phân giác của tam giác đó. Tại sao bốn điểm vừa vẽ là bốn đỉnh của một hình thoi?

Lời giải:

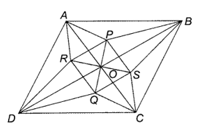
Gọi P, Q lần lượt là giao điểm ba đường phân giác của tam giác OAB, OCD thì O, P, Q thẳng hàng trên đường phân giác của góc AOB .

Do ABCD là hình bình hành nên AB // CD, AD // BC

Suy ra $\widehat{ODC}=\widehat{OBA};\widehat{OCD}=\widehat{OAB}$ (các cặp góc ở vị trí so le trong)

Mà DQ, BP lần lượt là tia phân giác của $\widehat{ODC};\widehat{OBA}$ nên $\widehat{OBP}=\widehat{ODQ}$

Xét ∆OBP và ∆ODQ có:

$\widehat{OBP}=\widehat{ODQ}$; OB = OD; $\widehat{BOP}=\widehat{QOD}$(đối đỉnh)

Do đó ∆OBP = ∆ODQ (g.c.g)

Suy ra OP = OQ, hay O là trung điểm của PQ

Gọi R, S lần lượt là giao điểm ba đường phân giác của tam giác OAD, OBC thì tương tự như trên, ta cũng chứng minh được O là trung điểm của RS và đường thẳng RS là đường phân giác của góc $\widehat{AOD}.$

Do góc AOB và góc AOD là hai góc kề bù nên hai đường phân giác PQ, RS vuông góc với nhau.

Tứ giác PSQR có hai đường chéo cắt nhau tại trung điểm của mỗi đường và vuông góc với nhau nên là hình thoi.

Bài 3.25 trang 42 sách bài tập Toán 8 Tập 1: Cho hình vuông ABCD. Với điểm M nằm giữa C và D, kẻ tia phân giác của góc DAM; nó cắt CD ở N. Đường thẳng qua N vuông góc với AM cắt BC ở P. Tính số đo của góc NAP.

Lời giải:

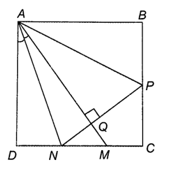
Đường thẳng NP ⊥ AM cắt AM ở Q.

Do ABCD là hình vuông nên ND ⊥ AD.

Xét ∆ADN vuông tại D và ∆AQN vuông tại Q có:

AN là cạnh chung, $\widehat{NAD}=\widehat{NAQ}$ (do AN là tia phân giác của )

Do đó ∆ADN = ∆AQN (cạnh huyền – góc nhọn)

Suy ra AD = AQ;

Mà AD = AB nên AQ = AB

Xét DAQP vuông tại Q và DABP vuông tại B có:

Cạnh AP chung; AQ = AB

Do đó ∆AQP = ∆ABP (cạnh huyền – cạnh góc vuông)

Suy ra $\widehat{QAP}=\widehat{BAP}$.

Ta có: $\widehat{BAD}=\widehat{DAN}+\widehat{NAQ}+\widehat{QAP}+\widehat{BAP}$

Mà $\widehat{NAD}=\widehat{NAQ};$ $\widehat{QAP}=\widehat{BAP}$ nên ta có:

$\widehat{BAD}=2\left(\widehat{NAQ}+\widehat{PAQ}\right)=2\widehat{NAP}$

Suy ra $\widehat{NAP}=\frac{1}{2}\widehat{DAB}=\frac{1}{2}\cdot 90°=45°.$

Bài 3.26 trang 42 sách bài tập Toán 8 Tập 1: Cho hình vuông ABCD với tâm O và có cạnh bằng 2 cm. Hai tia Ox, Oy tạo thành góc vuông. Tính diện tích của phần hình vuông nằm bên trong góc xOy.

Lời giải:

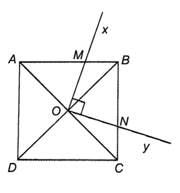
Tia Ox phải cắt một cạnh của hình vuông, giả sử Ox cắt cạnh AB tại M.

• Khi M trùng với A hay B thì tia Oy phải qua một đỉnh của hình vuông và dễ thấy phần hình vuông nằm trong góc xOy là một phần tư của hình vuông.

• Khi M nằm giữa A và B thì tia Oy phải cắt cạnh BC hoặc cạnh AD; giả sử Oy cắt BC tại N thì N nằm giữa B và C.

Do ABCD là hình vuông nên AC và BD là các đường phân giác các góc của hình vuông, BD ⊥ AC.

Suy ra $\widehat{MAO}=\widehat{NBO}$ (cùng phụ với $\widehat{MBO}$)

Ta có: $\widehat{MOA}+\widehat{MOB}=90°$, $\widehat{NOB}+\widehat{MOB}=90°$

Suy ra $\widehat{MOA}=\widehat{NOB}$

Xét ∆OAM và ∆OBN có:

$\widehat{MAO}=\widehat{NBO}$ ; OA = OB; $\widehat{MOA}=\widehat{NOB}$

Do đó ∆OAM = ∆OBN (g.c.g), nên hai tam giác này có cùng diện tích.

Ta có: diện tích phần hình vuông nằm trong góc xOy là diện tích tứ giác OMBN

Mà S_OMBN = S_OBM + S_OBN; S_OAB = S_OAM + S_OBM

Suy ra S_OMBN = S_OAB

Tức diện tích phần hình vuông nằm trong góc xOy bằng $\frac{1}{4}$ diện tích hình vuông.

• Cũng lập luận tương tự khi N nằm giữa A và D.

Vậy trong mọi trường hợp diện tích cần tìm bằng $\frac{1}{4}\cdot 2^2=1 \left({\text{cm}}^2\right)$.

Bài 3.27 trang 42 sách bài tập Toán 8 Tập 1: Xét tam giác ABC vuông cân tại A. Lấy trên cạnh BC hai điểm D, E sao cho BD = DE = EC. Lấy các điểm F, G lần lượt thuộc cạnh AC, AB sao cho FE, GD vuông góc với BC. Chứng minh tứ giác DEFG là một hình vuông.

Lời giải:

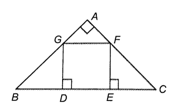
Do ∆ABC vuông cân tại A nên $\widehat{B}=\widehat{C}=45°$.

Xét ∆GBD vuông tại D và ∆EFC vuông tại E có:

BD = EC; $\widehat{B}=\widehat{C}$

Do đó ∆GBD = ∆FCE (cạnh góc vuông – góc nhọn kề)

Suy ra $\widehat{DGB}=\widehat{EFC}$

Mà $\widehat{B}+\widehat{DGB}=90°$ nên $\widehat{DGB}=90°-\widehat{B}=90°-45°=45°$

Do đó $\widehat{DGB}=\widehat{EFC}=45°$

Suy ra ∆GBD vuông cân tại D và ∆EFC vuông cân tại E.

Vì vậy GD = BD, EF = EC.

Mà $BD=DE=EC=\frac{1}{3}BC$

Suy ra GD = DE = EF.

Do GD ⊥ BC, EF ⊥ BC nên GD // EF

Tứ giác GDEF có GD // EF, GD = EF nên GDEF là hình chữ nhật.

Lại có GD và DE là hai cạnh kề của hình chữ nhật GDEF bằng nhau nên GDEF là hình vuông.

Xem thêm các bài giải sách bài tậpToán lớp 8 Kết nối tri thức hay, chi tiết khác:

SBT Toán 8 (Kết nối tri thức) Bài 13: Hình chữ nhật

SBT Toán 8 (Kết nối tri thức) Bài tập cuối chương 3

SBT Toán 8 (Kết nối tri thức) Bài 15: Định lí Thalès trong tam giác

SBT Toán 8 (Kết nối tri thức) Bài 16: Đường trung bình của tam giác

SBT Toán 8 (Kết nối tri thức) Bài 17: Tính chất đường phân giác của tam giác