a) Khảo sát sự biến thiên và vẽ đồ thị (H) của hàm số y = \(\frac{{2x - 1}}{{x - 1}}\). Tìm tọa độ tâm đối xứng I của đồ thị.
b) Tìm điều kiện của tham số m để đường thẳng d: y = −x + m cắt đồ thị (H) tại hai điểm phân biệt.
c) Chứng minh rằng tiếp tuyến của đồ thị (H) tại mọi điểm M thuộc (H) luôn cắt hai tiệm của (H) tại hai điểm A và B thuộc hai nhánh của đồ thị và đoạn AB ngắn nhất.
Giải bởi Vietjack
a) Tập xác định: D = ℝ\{1}.
Chiều biến thiên: y' = \(\frac{{ - 1}}{{{{\left( {x - 1} \right)}^2}}}\) < 0, ∀x ≠ 1.
Vậy hàm số nghịch biến trên mỗi khoảng xác định (−∞; 1) và (1; +∞).
Hàm số không có cực trị.
Giới hạn tại vô cực: \(\mathop {\lim }\limits_{x \to - \infty } y = 2\); \(\mathop {\lim }\limits_{x \to + \infty } y = 2\). Vậy đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số.
Giới hạn vô cực: \(\mathop {\lim }\limits_{x \to {1^ - }} y = - \infty \); \(\mathop {\lim }\limits_{x \to {1^ + }} y = + \infty \). Vậy đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.
Ta có bảng biến thiên:
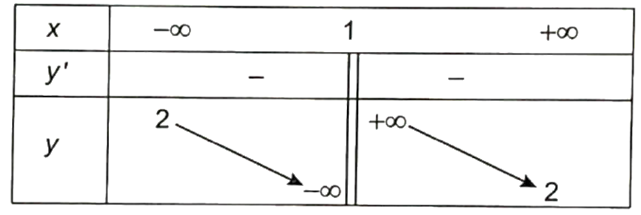
Đồ thị hàm số nhận giao điểm I(1; 2) của hai đường tiệm cận làm tâm đối xứng.
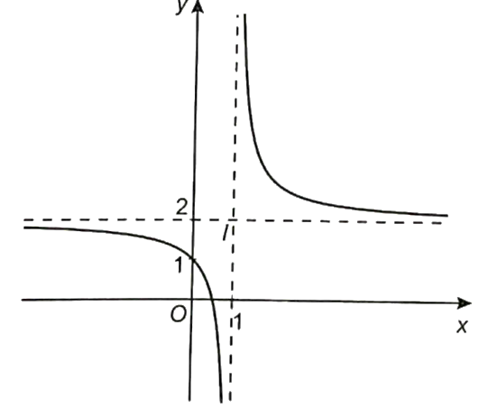
b) Đường thẳng thẳng d: y = −x + m cắt đồ thị (H): y = \(\frac{{2x - 1}}{{x - 1}}\) tại hai điểm phân biệt khi và chỉ khi phương trình \(\frac{{2x - 1}}{{x - 1}}\) = −x + m có hai nghiệm phân biệt khác 1.
Ta có: \(\frac{{2x - 1}}{{x - 1}}\) = −x + m
⇔ 2x − 1 = (x – 1)(−x + m).
⇔ x2 + (1 – m)x + m – 1 = 0 (x ≠ 1)
⇔ \(\left\{ \begin{array}{l}\Delta = {\left( {1 - m} \right)^2} - 4\left( {m - 1} \right) > 0\\1 + 1 - m + m - 1 \ne 0\end{array} \right.\) ⇔ m2 – 6m + 5 > 0 ⇔ m ∈ (−∞; 1) ∪ (5; +∞).
c)
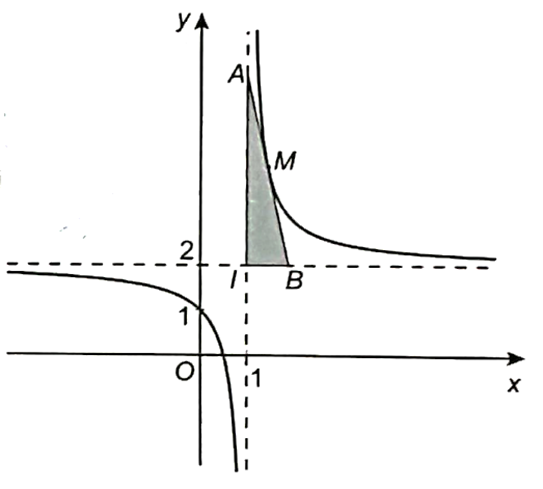
Lấy điểm M\(\left( {t;\frac{{2t - 1}}{{t - 1}}} \right)\) bất kì thuộc đồ thị (H) với t ≠ 1. Phương trình tiếp tuyến của đồ thị (H) tại tiếp điểm M là
∆: y = y'(t)(x – t) + y(t) hay y = \(\frac{{ - 1}}{{{{\left( {t - 1} \right)}^2}}}\left( {x - t} \right) + \frac{{2t - 1}}{{t - 1}}\).
Đường thẳng ∆ cắt tiệm cận đứng tại A\(\left( {1;\frac{{2t}}{{t - 1}}} \right)\). Ta có: IA = \(\frac{2}{{\left| {t - 1} \right|}}\).
Đường thẳng ∆ cắt tiệm cận ngang tại điểm B(2t – 1; 2). Ta có IB = 2\(\left| {t - 1} \right|\).
Vậy diện tích tam giác IAB là \({S_{\Delta IAB}} = \frac{1}{2}IA.IB = \frac{1}{2}.\frac{2}{{\left| {t - 1} \right|}}.2\left| {t - 1} \right| = 2\) (đvdt).
Giải SBT Toán 12 Tập 2 KNTT Bài tập ôn tập cuối năm có đáp án
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số y = \( - \frac{{{x^2} + x + 1}}{x}\).
b) Tìm các giá trị của tham số m để đường thẳng d: y = −2x + m cắt đồ thị (C) tại hai điểm A và B thuộc hai nhánh của đồ thị và đoạn AB ngắn nhất.
Giao hai con xúc xắc cân đối, đồng chất. Biết rằng số chấm trên hai con xúc xắc bé hơn 5. Xác suất để tổng số chấm bằng 6 là
A. \(\frac{3}{{17}}\).
B. \(\frac{4}{{17}}\).
C. \(\frac{5}{{19}}\).
D. \(\frac{3}{{16}}\).
Một hình chóp tứ giác đều ngoại tiếp hình cầu bán kính R.
a) Chứng minh rằng thể tích của khối chóp tương ứng và V = \(\frac{{4{R^2}{x^2}}}{{3\left( {x - 2R} \right)}}\), trong đó x là chiều cao của hình chóp.
b) Với giá trị nào của x để khối chóp tương ứng có thể tích nhỏ nhất?
Tính diện tích hình phẳng giới hạn bởi các đường y = \(\sqrt x \) − 2, trục hoành và các đường thẳng x = 4, x = 9.
Một ô tô đang chạy với vận tốc 15 m/s thì tăng tốc, chuyển động nhanh dần đều với gia tốc a = 3t – 8 (m/s2), trong đó t là khoảng thời gian tính bằng giây kể từ lúc tăng vận tốc.
a) Biết vận tốc của ô tô là v(t) = \(\frac{a}{2}\)t2 + bt + c, với a, b, c là các số nguyên.
Tính giá trị a + b + c.
b) Quãng đường ô tô đi được sau 10 giây kể từ lúc bắt đầu tăng tốc là bao nhiêu mét? (Làm tròn kết quả đến hàng đơn vị).
Cho f(x) là một hàm số liên tục trên đoạn [a; b] và F(x) là một nguyên hàm của f(x) trên [a; b]. Khi đó \(\int\limits_a^b {f\left( x \right)dx} \)có giá trị bằng
A. F(b) – F(a).
B. F(b) – F(a) + C; C là hằng số.
C. F(a) – F(b).
D. F(a) – F(b) + C; C là hằng số.
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC) và tam giác ABC vuông cân tại B, biết SA = AB = BC = a. Gọi M là trung điểm của cạnh AC. Tính tích vô hướng \(\overrightarrow {SM} .\overrightarrow {BC} \) bằng
A. \(\frac{{{a^2}}}{2}\).
B. a2.
C. −a2.
D. \( - \frac{{{a^2}}}{2}\).
Tính:
a) \(\int\limits_0^{\frac{\pi }{4}} {{{\sin }^2}\frac{x}{2}dx} \);
b) \(\int\limits_0^1 {\left( {3x - 4{x^3}} \right)dx - \int\limits_1^2 {\left( {4{x^3} - 3x} \right)dx} } \);
c) \(\int\limits_0^6 {\left( {\left| {2x - 2} \right| + 4{x^2}} \right)dx} \).
Chọn ngẫu nhiên gia đình có 2 con. Biết rằng người con đầu là con gái. Xác suất để gia đình đó có hai con gái là
A. 0,6.
B. 0,5.
C. 0,55.
D. 0,65.
Tính thể tích khối tròn xoay tạo thành khi quay quanh Ox hình phẳng giới hạn bởi đường parabol y = x2 – 3x + 2, trục hoành và các đường thẳng x = 1,x = 2.
a) Lập bảng biến thiên của hàm số y = \(\frac{{{x^2}}}{{x + 1}}\).
b) Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức M = \(\frac{{{{\cos }^2}\alpha }}{{\cos \alpha + 1}}\).
a) Khảo sát sự biến thiên và vẽ đồ thị hàm số y = −x3 + 3x2 – 2.
b) Tìm điều kiện của tham số m để phương trình x3 – 3x2 + 5 – m = 0 có ba nghiệm phân biệt.
c) Tìm điểm thuộc đồ thị hàm số mà tiếp tuyến với đồ thị tại điểm có hệ số góc lớn nhất.
Cho \(\int\limits_0^4 {f\left( x \right)dx = 5} \) và \(\int\limits_0^4 {g\left( x \right)dx = 6} \). Giá trị của \(\int\limits_0^4 {\left[ {f\left( x \right) + 2g\left( x \right)} \right]dx} \) là
A. 17.
B. 16.
C. 11.
D. 22.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.
