Cho hai đồ thị hàm số y=sin(x+π4) và y=sinx.
a) Phương trình hoành độ giao điểm của hai đồ thị hàm số: sin(x+π4)=sinx.
b) Hoành độ giao điểm của hai đồ thị là x=3π8+kπ(k∈Z).
c) Khi x∈[0;2π] thì hai đồ thị hàm số cắt nhau tại ba điểm.
d) Khi x∈[0;2π] thì toạ độ giao điểm của hai đồ thị hàm số là: (5π8;sin5π8),(7π8;sin7π8).
 Giải bởi Vietjack
Giải bởi Vietjack
Phương trình hoành độ giao điểm của hai đồ thị hàm số:
sin(x+π4)=sinx⇔[x+π4=x+k2πx+π4=π−x+k2π⇔x=3π8+kπ (k∈ℤ)
Vì x∈[0;2π]⇒x∈{3π8;11π8} .
Với x=3π8⇒y=sin3π8≈0,92 ; với x=11π8⇒y=sin11π8≈−0,92 .
Vậy toạ độ giao điểm của hai đồ thị hàm số là:(3π8;sin3π8),(11π8;sin11π8) .
Đáp án: a) Đúng, b) Đúng, c) Sai, d) Sai.
43 bài tập Phương trình và bất phương trình có lời giải
Cho phương trình sin(2x−π4)=sin(x+3π4) (*).
a) Phương trình có nghiệm: x=π+k2π và x=π6+k2π3(k∈Z).
b) Trong khoảng (0;π), phương trình có 2 nghiệm.
c) Tổng các nghiệm của phương trình trong khoảng (0;π) bằng 7π6.
d) Trong khoảng (0;π), phương trình có nghiệm lớn nhất bằng 5π6.
Cho phương trình lượng giác cot3x=−1√3 (*).
a) Phương trình (*) tương đương cot3x=cot(−π6).
b) Phương trình (*) có nghiệm x=π9+kπ3(k∈Z).
c) Tổng các nghiệm của phương trình trong khoảng (−π2;0) bằng −5π9.
d) Phương trình có nghiệm dương nhỏ nhất bằng 2π9.
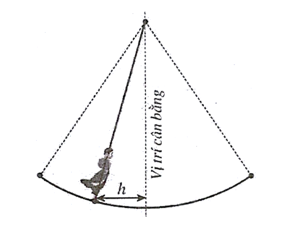
a) Vật ở xa vị trí cân bằng nhất nghĩa là h=1,5m.
b) Trong 10 giây đầu tiên, có hai thời điểm vật ở xa vị trí cân bằng nhất.
c) Khi vật ở vị trí cân bằng thì cos(tπ4)=0.
d) Trong khoảng từ 0 đến 20 giây thì vật đi qua vị trí cân bằng 4 lần.
Cho phương trình tan(2x−15∘)=1 (*).
a) Phương trình (*) có nghiệm x=30∘+k90∘(k∈Z).
b) Phương trình có nghiệm âm lớn nhất bằng −30∘.
c) Tổng các nghiệm của phương trình trong khoảng (−180∘;90∘) bằng 180∘.
d) Trong khoảng (−180∘;90∘), phương trình có nghiệm lớn nhất bằng 60∘.
Cho phương trình log3(x+6)=log3(x−1)+1 (*).
a) Điều kiện xác định của phương trình: x>1.
b) Phương trình (*) có chung tập nghiệm với phương trình x2−11x+9x−1=0.
c) Gọi x=a là nghiệm của phương trình (*), khi đó lim.
d) Nghiệm của phương trình (*) là hoành độ giao điểm của đường thẳng {d_1}:2x - y - 8 = 0 với đường thẳng {d_2}:y = 0.
Một cây cầu có dạng cung AB của đồ thị hàm số y = 4,8\cos \frac{x}{9} và được mô tả trong hệ trục toạ độ với đơn vị trục là mét như ở hình vẽ dưới đây.
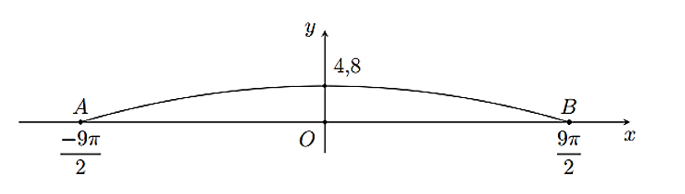
Một sà lan chở khối hàng hoá được xếp thành hình hộp chữ nhật với độ cao 3,6\,{\rm{m}} so với mực nước sông. Hỏi chiều rộng của khối hàng hoá đó lớn nhất là bao nhiêu mét để sà lan có thể đi qua được gầm cầu (làm tròn kết quả đến hàng đơn vị)?
Số nghiệm nguyên của bất phương trình {\log _{\frac{\pi }{4}}}\left( {3x + 1} \right) \ge {\log _{\frac{\pi }{4}}}\left( {2x + 5} \right) là
Phương trình \tan \left( {3x - 15^\circ } \right) = \sqrt 3 có các nghiệm là
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.