Cho phương trình lượng giác cot3x=−1√3 (*).
a) Phương trình (*) tương đương cot3x=cot(−π6).
b) Phương trình (*) có nghiệm x=π9+kπ3(k∈Z).
c) Tổng các nghiệm của phương trình trong khoảng (−π2;0) bằng −5π9.
d) Phương trình có nghiệm dương nhỏ nhất bằng 2π9.
 Giải bởi Vietjack
Giải bởi Vietjack
Ta có cot3x=−1√3⇔cot3x=cot(−π3)⇔3x=−π3+kπ⇔x=−π9+kπ3 (k∈ℤ).
−π2<−π9+kπ3<0 (k∈ℤ)⇔−76<k<13⇒k={−1;0}⇒[x=−π9x=−4π9.
Đáp án: a) Sai, b) Sai, c) Đúng, d) Đúng.
43 bài tập Phương trình và bất phương trình có lời giải
Cho phương trình log3(x+6)=log3(x−1)+1 (*).
a) Điều kiện xác định của phương trình: x>1.
b) Phương trình (*) có chung tập nghiệm với phương trình x2−11x+9x−1=0.
c) Gọi x=a là nghiệm của phương trình (*), khi đó limx→a(x−3)=52.
d) Nghiệm của phương trình (*) là hoành độ giao điểm của đường thẳng d1:2x−y−8=0 với đường thẳng d2:y=0.
Gọi x1,x2 là hai nghiệm của phương trình 7x+1=(17)x2−2x−3. Khi đó x21+x22 bằng
Cho phương trình sin(2x−π4)=sin(x+3π4) (*).
a) Phương trình có nghiệm: x=π+k2π và x=π6+k2π3(k∈Z).
b) Trong khoảng (0;π), phương trình có 2 nghiệm.
c) Tổng các nghiệm của phương trình trong khoảng (0;π) bằng 7π6.
d) Trong khoảng (0;π), phương trình có nghiệm lớn nhất bằng 5π6.
Cho hai đồ thị hàm số y=sin(x+π4) và y=sinx.
a) Phương trình hoành độ giao điểm của hai đồ thị hàm số: sin(x+π4)=sinx.
b) Hoành độ giao điểm của hai đồ thị là x=3π8+kπ(k∈Z).
c) Khi x∈[0;2π] thì hai đồ thị hàm số cắt nhau tại ba điểm.
d) Khi x∈[0;2π] thì toạ độ giao điểm của hai đồ thị hàm số là: (5π8;sin5π8),(7π8;sin7π8).
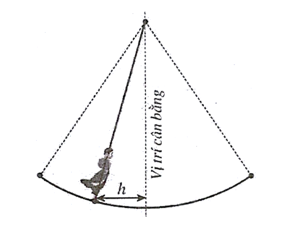
a) Vật ở xa vị trí cân bằng nhất nghĩa là h=1,5m.
b) Trong 10 giây đầu tiên, có hai thời điểm vật ở xa vị trí cân bằng nhất.
c) Khi vật ở vị trí cân bằng thì cos(tπ4)=0.
d) Trong khoảng từ 0 đến 20 giây thì vật đi qua vị trí cân bằng 4 lần.
Cho phương trình tan(2x−15∘)=1 (*).
a) Phương trình (*) có nghiệm x=30∘+k90∘(k∈Z).
b) Phương trình có nghiệm âm lớn nhất bằng −30∘.
c) Tổng các nghiệm của phương trình trong khoảng (−180∘;90∘) bằng 180∘.
d) Trong khoảng (−180∘;90∘), phương trình có nghiệm lớn nhất bằng 60∘.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.