Danh sách câu hỏi
Có 8,363 câu hỏi trên 210 trang
0
lượt xem
0
lượt xem
0
lượt xem
0
lượt xem
0
lượt xem
0
lượt xem
30
lượt xem
26
lượt xem
23
lượt xem
20
lượt xem
21
lượt xem
20
lượt xem
23
lượt xem
20
lượt xem
9
lượt xem
20
lượt xem
20
lượt xem
8
lượt xem
8
lượt xem
14
lượt xem
19
lượt xem
15
lượt xem
20
lượt xem
21
lượt xem
19
lượt xem
25
lượt xem
7
lượt xem
7
lượt xem
12
lượt xem
10
lượt xem
10
lượt xem
13
lượt xem
9
lượt xem
11
lượt xem
7
lượt xem



 độ cao của lần rơi trước. Giả sử quả bóng luôn chuyển động vuông góc với mặt đất. Tổng quãng đường bóng đã di chuyển (từ lúc bắt đầu thả đến lúc bóng không di chuyển nữa) gần nhất với kết quả nào sau đây?
độ cao của lần rơi trước. Giả sử quả bóng luôn chuyển động vuông góc với mặt đất. Tổng quãng đường bóng đã di chuyển (từ lúc bắt đầu thả đến lúc bóng không di chuyển nữa) gần nhất với kết quả nào sau đây? . Tính tổng
. Tính tổng 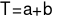
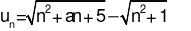 , trong đó a là tham số thực. Tìm a để
, trong đó a là tham số thực. Tìm a để 
 bằng:
bằng: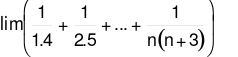 là:
là: là:
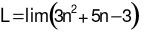
là: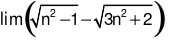 bằng
bằng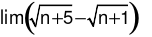 bằng
bằng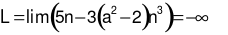
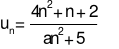 trong đó a là tham số thực. Để dãy số có giới hạn bằng 2, giá trị của a là
trong đó a là tham số thực. Để dãy số có giới hạn bằng 2, giá trị của a là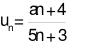 trong đó a là tham số thực. Để dãy số có giới hạn bằng 2, giá trị của a là
trong đó a là tham số thực. Để dãy số có giới hạn bằng 2, giá trị của a là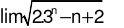 bằng:
bằng: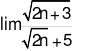 bằng:
bằng: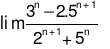 bằng:
bằng: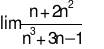 bằng:
bằng: