Toptailieu.vn biên soạn và giới thiệu giải Sách bài tập Toán 11 Bài 4: Khoảng cách trong không gian sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập trong SBT Toán 11 Bài 4.

SBT Toán 11 (Chân trời sáng tạo) Bài 4: Khoảng cách trong không gian

Bài 1 trang 68 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có đáy ABC là tam giác đều canh a, cạnh bên SA vuông góc với đáy. Tính khoảng cách từ điểm A đến mặt phẳng (SBC) theo a, biết SA = $\frac{a\sqrt{6}}{2}$ .

Lời giải:

Gọi E là trung điểm của BC thì BC ⊥ AE (vì ∆ABC đều).

Ta có BC ⊥ SA và BC ⊥ AE $\Rightarrow$ BC ⊥ (SAE).

$\Rightarrow$(SBC) ⊥ (SAE).

Trong mặt phẳng (SAE), vẽ AF ⊥ SE (F $\in$ SE).

Suy ra AF ⊥ (SBC) hay d(A, (SBC))=AF.

Xét ∆SAE vuông tại A, ta có:

$\frac{1}{A{F}^2}=\frac{1}{A{S}^2}+\frac{1}{A{E}^2}=\frac{2}{3a^2}+\frac{4}{3a^2}=\frac{2}{a^2}\Rightarrow AF=\frac{a\sqrt{2}}{2}$.

Vậy $d\left(S,\left(ABC\right)\right)=AF=\frac{a\sqrt{2}}{2}$ .

Bài 2 trang 68 SBT Toán 11 Tập 2: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Gọi G là trọng tâm của tam giác ABC, M là trung điểm của SC.

a) Tính khoảng cách từ S đến mặt phẳng (ABC).

b) Tính khoảng cách từ M đến mặt phẳng (SAG).

Lời giải:

a)Do S.ABC là hình chóp tam giác đều nên SG ⊥ (ABC) hay d(S, (ABC))=SG.

Tam giác ABC là tam giác đều cạnh 3a nên

$AG=\frac{2}{3}.\frac{3a\sqrt{3}}{2}=a\sqrt{3}$

Tam giác SAG vuông tại G nên

$SG=\sqrt{S{A}^2-A{G}^2}=\sqrt{4a^2-3a^2}=a$

Vậy d(S, (ABC)) = a.

b) Vì SC $\cap$ (SAG) = S nên $\frac{d(M,(SAG\left)\right)}{d(C,(SAG\left)\right)}=\frac{MS}{CS}=\frac{1}{2}$

$\Rightarrow d(M,(SAG\left)\right)=\frac{1}{2}d(C,(SAG\left)\right)$

Gọi I là trung điểm của BC.

Ta có: CB ⊥ AI và CB ⊥ SG

$\Rightarrow$ CB ⊥ (SAG) và CB $\cap$ (SAG) = I.

Do đó $d(C,(SAG\left)\right)=CI=\frac{1}{2}BC=\frac{3a}{2}$ .

Vậy $d(M,(SAG\left)\right)=\frac{3a}{4}$ .

Bài 3 trang 68 SBT Toán 11 Tập 2: Cho hình lập phương $ABCD.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$ cạnh a. Gọi M, N lần lượt là trung điểm của AC và $B^{\text{'}}{C}^{\text{'}}$ . Tính khoảng cách giữa hai đường thẳng MN và $B^{\text{'}}{D}^{\text{'}}$ .

Lời giải:

B'D' $\cap$ A'C' tại O.

Gọi P là trung điểm của OC'.

Vě OH ⊥ MP, HE // NP, EF // OH.

ABCD là hình lập phương, ta dễ dàng có được: B'D' ⊥ (A'C'CA).

Hay B'D' ⊥ OH, mà OH // EF

$\Rightarrow$ EF ⊥ B'D' (1).

NP // B'D' $\Rightarrow$ NP ⊥ (A'C'CA) hay NP ⊥ OH.

Đồng thời OH ⊥ MP.

$\Rightarrow$ OH ⊥ (MNP) hay OH ⊥ MN $\Rightarrow$ EF ⊥ MN (2)

Từ (1) và (2) ta có: d(MN, B'D') = EF = OH.

Xét tam giác vuông MOP, ta có OM = a, OP = $\frac{a\sqrt{2}}{4}$, suy ra OH = $\frac{a}{3}$ .

Vậy d(MN, B'D') = $\frac{a}{3}$ .

Bài 4 trang 68 SBT Toán 11 Tập 2: Cho hình tứ diện đều ABCD có cạnh bằng $\sqrt{11}$ . Gọi I là trung điểm của cạnh CD. Tính khoảng cách giữa hai đường thẳng AC và BI.

Lời giải:

Gọi O là trung điểm AC, J là trung điểm OD.

Vě OH ⊥ BJ, HE // AC, EF // OH.

Có IJ // AC nên AC // (BIJ).

$\Rightarrow$ d(AC, BI) = d(AC, (BIJ)) = d(O, (BIJ)).

Do ABCD là tứ diện đều nên ta dễ dàng nhận ra AC ⊥ (OBD).

$\Rightarrow$ AC ⊥ OH (OH $\subset$ OBD).

AC // IJ, $\Rightarrow$ OH ⊥ IJ.

Kết hợp giả thiết, suy ra OH ⊥ (BIJ) hay d(O, (BIJ)) = OH.

Xét tam giác OBD cân tại O, ta có

$\begin{array}{c}BD=\sqrt{11}.\\ OB=OD=BD.\frac{\sqrt{3}}{2}=\frac{\sqrt{33}}{2}\\ \Rightarrow BJ=\frac{\sqrt{11}}{4}\end{array}$.

Áp dụng công thức Heron, ta có:

$S_{OBD}=\frac{11\sqrt{2}}{4}\Rightarrow S_{OBJ}=\frac{11\sqrt{2}}{4}.$

Ta tính được OH = $\sqrt{2}$.

Vậy khoảng cách giữa hai đường thẳng AC và BI là $\sqrt{2}$ .

Bài 5 trang 68 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có tam giác vuông cân tại B, AC = $a\sqrt{2}$ , mặt phẳng (SAC) vuông góc với mặt đáy (ABC). Các mặt bên (SAB), (SBC) tạo với mặt đáy các góc bằng nhau và bằng 60°. Tính theo a thể tích V của khối chóp S.ABC.

Lời giải:

Ta có: (SAC) ⊥ (ABC) và (SAC) $\cap$ (ABC) = AC.

Trong mặt phẳng (SAC), vẽ SH ⊥ AC (H $\in$ AC) thì SH ⊥ (ABC).

Gọi I, K lần lượt là hình chiếu vuông góc của H lên cạnh AB và BC.

Khi đó, ta có $\left(\left(SAB\right),\left(ABC\right)\right)=\widehat{SIH},\left(\left(SBC\right),\left(ABC\right)\right)=\widehat{SKH}.$

Mà $\widehat{SIH}=\widehat{SKH}=60°$ nên HI = HK.

Suy ra tử giác BIHK là hình vuông nên H là trung điểm cạnh AC.

Khi đó tử giác BIHK là hình vuông cạnh $\frac{a}{2}$ .

SH = HI . tan 60° = $\frac{a\sqrt{3}}{2}$.

$\Rightarrow V_{S.BCD}=\frac{1}{3}.S_{BCD}.SA=\frac{1}{3}.\frac{a^2}{2}.a\sqrt{3}=\frac{a^2\sqrt{3}}{6}$.

Vậy thể tích V của khối chóp S.ABC là $\frac{a^2\sqrt{3}}{6}$.

Bài 6 trang 68 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD) và SA = $a\sqrt{3}$, đáy ABCD là hình thang vuông tại A và B có AB = a, AD = 3a, BC = a. Tính thể tích khối chóp S.BCD theo a.

Lời giải:

Ta có: $S_{ABCD}=\frac{1}{2}.AB.(AD+BC)=\frac{1}{2}.a.(3a+a)=2a^2$

Lại có: $S_{ABD}=\frac{1}{2}.AB.AD=\frac{1}{2}.a.3a=\frac{3a^2}{2}$

Suy ra $S_{BCD}=S_{ABCD}-S_{ABD}=\frac{a^2}{2}$ .

Vậy $V_{S.BCD}=\frac{1}{3}.S_{BCD}.SA=\frac{1}{3}.\frac{a^2}{2}.a\sqrt{3}=\frac{a^2\sqrt{3}}{6}$ .

Bài 7 trang 68 SBT Toán 11 Tập 2: Cho hình lăng trụ đều $ABC.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}$ có cạnh đáy bằng a. Biết $d\left(A\right(A^{\text{'}}B{C}^{\text{'}}\left)\right)=\frac{a\sqrt{57}}{12}$ . Tính $V_{ABC.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}$ .

Lời giải:

Gọi I là trung điểm của BC và H là hình chiếu của A trên A'I.

Ta có: BC ⊥ AI và BC ⊥ AA' $\Rightarrow$ BC ⊥ (A'AI) $\Rightarrow$ (A'BC) ⊥ (A'AI).

Mặt khác (AB'C) $\cap$ (A'AI) = A'I và AH ⊥ A'I.

Nên $d(A,(A\text{'}BC\left)\right)=AH=\frac{a\sqrt{57}}{12}$

∆ABC đều cạnh a $\Rightarrow AI=\frac{a\sqrt{3}}{2}$ và $S_{ABC}=\frac{a^2\sqrt{3}}{4}$

Xét tam giác A'AI vuông tại A, ta có:

$\frac{1}{A\text{'}{A}^2}=\frac{1}{A{H}^2}-\frac{1}{A{I}^2}=\frac{144}{57a^2}-\frac{4}{3a^2}=\frac{68}{57a^2}\Rightarrow AA\text{'}=\frac{a\sqrt{57}}{2\sqrt{17}}$.

Do đó $V_{ABC.A\text{'}B\text{'}C\text{'}}=S_{ABC}.AA\text{'}=\frac{a^2\sqrt{3}}{4}.\frac{a\sqrt{57}}{2\sqrt{17}}=\frac{a^3\sqrt{171}}{8\sqrt{17}}$

Vậy $V_{ABC.A\text{'}B\text{'}C\text{'}}=\frac{a^3\sqrt{171}}{8\sqrt{17}}$.

Bài 8 trang 68 SBT Toán 11 Tập 2: Một hình hộp chữ nhật $ABCD.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$ có ba kích thước là 2 cm, 3 cm và 6 cm. Tính thể tích của khối tứ diện $AC{B}^{\text{'}}{D}^{\text{'}}$ .

Lời giải:

Ta có:

$$\begin{gathered} V_{ABCD.A\text{'}B\text{'}C\text{'}D\text{'}}=V_{BAB\text{'}C}+V_{D.ACD\text{'}}+V_{A\text{'}B\text{'}AD\text{'}}+V_{C\text{'}B\text{'}CD\text{'}}+V_{ACB\text{'}D\text{'}} \\ =4.V_{BAB\text{'}C}+V_{ACB\text{'}D\text{'}} \end{gathered}$$

$$\begin{gathered} \Rightarrow V_{ACB\text{'}D\text{'}}=V_{ABCD.A\text{'}B\text{'}C\text{'}D\text{'}}-4.V_{BAB\text{'}C} \\ \Rightarrow V_{ACB\text{'}D\text{'}}=V_{ABCD.A\text{'}B\text{'}C\text{'}D\text{'}}-4.\frac{1}{6}.V_{ABCD.A\text{'}B\text{'}C\text{'}D\text{'}} \\ \Rightarrow V_{ACB\text{'}D\text{'}}=\frac{1}{3}{V}_{ABCD.A\text{'}B\text{'}C\text{'}D\text{'}} \end{gathered}$$

$\Rightarrow V_{ACB\text{'}D\text{'}}=\frac{1}{3}\mathrm{.2.3.6}=12\left(c{m}^3\right)$

Bài 9 trang 68 SBT Toán 11 Tập 2: Cho hình chóp cụt tam giác đều $ABC.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}$ có đường cao $H{H}^{\text{'}}=2a$ . Cho biết AB = 2a, $A^{\text{'}}{B}^{\text{'}}=a$ . Gọi B₁, C₁ lần lượt là trung điểm của AB, AC. Tính thể tích của:

a) Khối chóp cụt đều $ABC.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}$ .

b) Khối lăng trụ $A{B}_1{C}_1.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}$ .

Lời giải:

a)

Áp dụng công thức: $V=\frac{1}{3}h\left(S+\sqrt{SS\text{'}}+S\text{'}\right)$ ,

Do ABC, A¢B¢C¢ là các tam giác đều nên: 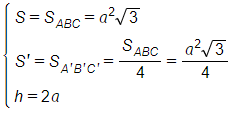 , thay vào công thức trên ta có:

$V=\frac{1}{3}.2a.\left(a^2\sqrt{3}+\sqrt{a^2\sqrt{3}.\frac{a^2\sqrt{3}}{4}}+\frac{a^2\sqrt{3}}{4}\right)$

$=\frac{2}{3}a.\left(\frac{5\sqrt{3}{a}^2}{4}+\sqrt{\frac{3a^4}{4}}\right)$$=\frac{2}{3}a.\left(\frac{5\sqrt{3}{a}^2}{4}+\frac{\sqrt{3}{a}^2}{2}\right)$

$=\frac{2}{3}a.\left(\frac{5\sqrt{3}{a}^2}{4}+\frac{\sqrt{3}{a}^2}{2}\right)=\frac{2}{3}a.\frac{7\sqrt{3}{a}^2}{4}=\frac{7a^3\sqrt{3}}{6}$.

b)Áp dụng công thức: $V\text{'}=S\text{'}.h\text{'}$ , với $S\text{'}=\frac{a^2\sqrt{3}}{4},h\text{'}=2a.$

Ta có: $V\text{'}=\frac{a^2\sqrt{3}}{4}.2a.=\frac{a^3\sqrt{3}}{2}$ .

Bài 10 trang 68 SBT Toán 11 Tập 2: Tính thể tích một cái sọt đựng đồ có dạng hình chóp cụt tứ giác đều, đáy lớn có cạnh bằng 80 cm, đáy nhỏ có cạnh bằng 40 cm và cạnh bên bằng 80 cm.

Lời giải:

Ta có: $OC=40\sqrt{2},O\text{'}C\text{'}=20\sqrt{2}$ , suy ra $CH=20\sqrt{2}$

Trong tam giác vuông C'CH có: $C\text{'}H=\sqrt{CC{\text{'}}^2-C{H}^2}=20\sqrt{14}$

Nên $OO\text{'}=C\text{'}H=20\sqrt{14}$

Thể tích của cái sọt đựng đồ là:

$V=\frac{1}{3}.20\sqrt{14}.(6400+\sqrt{6400.1600}+1600)\approx 279\mathrm{377,08}$ (cm³).