Trong mặt phẳng Oxy. Cho đường thẳng :ax+by+c=0(a2+b2>0)

Trong mặt phẳng Oxy. Cho đường thẳng :ax+by+c=0(a2+b2>0)

Hoàng Huyền Trang Ngày: 04-10-2022 Lớp 10

440

Với giải HĐ Khám phá 7 trang 56 Toán 10 Tập 2 Chân trời sáng tạo chi tiết trong Bài 2. Đường thẳng trong mặt phẳng tọa độ giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Trong mặt phẳng Oxy. Cho đường thẳng $∆$ :ax+by+c=0(a²+b²>0)

HĐ Khám phá 7 trang 56 Toán 10 Tập 2: Trong mặt phẳng Oxy. Cho đường thẳng $Δ : a x + b y + c = 0 (a^{2} + b^{2} > 0)$ có vectơ pháp tuyến $\vec{n}$ và cho điểm $M_{0} (x_{0}; y_{0})$ có hình chiếu vuông góc $H (x_{H}; y_{H})$ trên $Δ$ (hình 9).

a) Chứng minh rằng hai vectơ $\vec{n}$ và $\vec{H M_{0}}$ cùng phương và tìm tọa độ của chúng

b) Gọi p là tích vô hướng của hai vectơ $\vec{n}$ và $\vec{H M_{0}}$ .

Chứng minh rằng $p = a x_{0} + b y_{0} + c$

c) Giải thích công thức $| \vec{H M_{0}} | = \frac{| p |}{| \vec{n} |}$

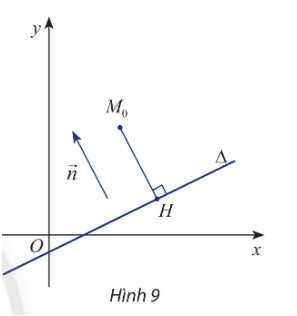
HĐ Khám phá 7 trang 56 Toán 10 Tập 2 Chân trời sáng tạo (ảnh 1)

Phương pháp giải:

a) So sánh phương với vectơ chỉ phương

b) Bước 1: Nhân tích vô hướng của hai vectơ

Bước 2: Thay tọa độ điẻm H vào đường thẳng tìm mối liên hệ

c) Thay vào công thức kết quả đã tìm được ở câu b)

Lời giải

a) Ta có: $\vec{n}$ và $\vec{H M_{0}} = (x_{0} - x_{H}; y_{0} - y_{H})$

Mà H là hình chiếu vuông góc của $M_{0}$ trên $Δ$ nên $H M_{0} ⊥ Δ$

Mặt khác vectơ pháp tuyến $\vec{n}$ cùng vuông góc với $Δ$

Suy ra $\vec{n}$ và $\vec{H M_{0}}$ cùng phương (đpcm)

b) Ta có: $\vec{n} = (a; b)$ và $\vec{H M_{0}} = (x_{0} - x_{H}; y_{0} - y_{H})$

Suy ra $p = \vec{n} . \vec{H M_{0}} = a (x_{0} - x_{H}) + b (y_{0} - y_{H}) = a x_{0} + b y_{0} - (a x_{H} + b y_{H})$ (1)

Mà H thuộc đường thẳng $Δ$ nên tọa độ điểm H thỏa mãn phương trình đường thẳng $Δ$

Thay tọa độ điểm H vào phương trình $Δ : a x + b y + c = 0 (a^{2} + b^{2} > 0)$ ta có:

$a x_{H} + b y_{H} + c = 0 \Leftrightarrow c = - (a x_{H} + b y_{H})$

Thay $c = - (a x_{H} + b y_{H})$ vào (1) ta có

$p = a x_{0} + b y_{0} + c$ (đpcm)

c) Ta có: $p = \vec{n} . \vec{H M_{0}} \Leftrightarrow \vec{H M_{0}} = \frac{p}{\vec{n}} \Rightarrow | \vec{H M_{0}} | = | \frac{p}{\vec{n}} | \Rightarrow | \vec{H M_{0}} | = \frac{| p |}{| \vec{n} |}$

Xem thêm các bài giải Toán 10 Chân trời sáng tạo hay, chi tiết khác:

HĐ Khởi động trang 46 Toán 10 Tập 2:...

HĐ Khám phá 1 trang 46 Toán 10 Tập 2: Trong mặt phẳng Oxy, cho hai đường thẳng $Δ$ đi qua điểm $M_{0} (x_{0}; y_{0})$ và vectơ $\vec{n} = (a; b)$ và $\vec{u} = (b; - a)$ khác vectơ 0. Cho biết $\vec{u}$ có giá song song hoặc trùng với $Δ$ ...

HĐ Khám phá 2 trang 47 Toán 10 Tập 2: Trong mặt phẳng Oxy, cho đường thẳng $Δ$ đi qua điểm $M_{0} (x_{0}; y_{0})$ và nhận $\vec{u} = (u_{1}; u_{2})$ là vectơ chỉ phương. Với mỗi điểm $M (x; y)$ thuộc $Δ$ , tìm tọa độ của điểm M theo tọa độ của $M_{0}$ và $\vec{u}$ ...

Thực hành 1 trang 47 Toán 10 Tập 2: a) Viết phương trình tham số của đường thẳng d đi qua điểm $B (- 9; 5)$ và nhận $\vec{v} = (8; - 4)$ là vectơ chỉ phương...

Vận dụng 1 trang 48 Toán 10 Tập 2: Một trò chơi đua xe ô tô vượt da mặt trên máy tính là xác định trước một hệ trục tọa độ Oxy. Cho biết một ô tô chuyển động thẳng đều từ điểm $M (1; 1)$ với Vectơ vận tốc $\vec{v} = (40; 30)$ ...

HĐ Khám phá 3 trang 48 Toán 10 Tập 2: Trong mặt phẳng Oxy, cho đường thẳng $Δ$ đi qua điểm $M_{0} (x_{0}; y_{0})$ và nhận $\vec{n} = (a; b)$ làm vectơ pháp tuyến. Với mỗi điểm $M (x; y)$ thuộc $Δ$ , chứng tỏ rằng điểm $M (x; y)$ có tọa độ thỏa mãn phương trình...

Thực hành 2 trang 49 Toán 10 Tập 2: Viết phương trình tham số và phương trình tổng quát của đường thẳng $Δ$ trong các trường hợp sau...

Vận dụng 2 trang 49 Toán 10 Tập 2: Một người đã lập trình một trò chơi trên máy tính. Trên màn hình máy tính đã xác định trước một hệ trục tọa độ Oxy. Người đó viết lệnh để một điểm $M (x; y)$ từ vị trí $A (1; 2)$ chuyển động thẳng đều với Vectơ vận tốc $\vec{v} = (3; - 4)$ ...

Thực hành 3 trang 51 Toán 10 Tập 2: Tìm các hàm số bậc nhất có đồ thị là các đường thẳng trong thực hành 2...

Vận dụng 3 trang 51 Toán 10 Tập 2: Một người bắt đầu mở một vòi nước. Nước từ vòi chảy với vận tốc là 2 $m^{3} / h$ vào một cái bể đã chứa sẵn 5 $m^{3}$ nước...

HĐ Khám phá 4 trang 51 Toán 10 Tập 2: Cho hai đường thẳng $Δ_{1}$ và $Δ_{2}$ một vectơ pháp tuyến lần lượt là $\vec{n_{1}}$ và $\vec{n_{2}}$ ...

Thực hành 4 trang 53 Toán 10 Tập 2: Xét vị trí tương đối của các cặp đường thẳng $d_{1}$ và $d_{2}$ trong các trường hợp sau...

Vận dụng 4 trang 53 Toán 10 Tập 2: Viết phương trình đường thẳng $d_{1}$ ...

HĐ Khám phá 5 trang 54 Toán 10 Tập 2: Cho hai đường thẳng xy và zt cắt nhau tại O và cho biết $\hat{x O z} = 38^{\circ}$ (hình 6)...

HĐ Khám phá 6 trang 54 Toán 10 Tập 2: Cho hai đường thẳng...

Thực hành 5 trang 56 Toán 10 Tập 2: Tìm số đo của góc giữa hai đường thẳng $Δ_{1}$ và $Δ_{2}$ trong các trường hợp sau...

Vận dụng 5 trang 56 Toán 10 Tập 2: Tìm số đo của góc giữa hai đường thẳng là đồ thị của hai hàm số $y = x$ và $y = 2 x + 1$ ...

Thực hành 6 trang 57 Toán 10 Tập 2: Trong mặt phẳng Oxy, cho tam giác ABC có tọa độ các đỉnh là $A (1; 1), B (5; 2), C (4; 4)$ . Tính độ dài các đường cao của tam giác ABC...

Vận dụng 6 trang 57 Toán 10 Tập 2: Tính khoảng cách giữa hai đường thẳng $d_{1} : 4 x - 3 y + 2 = 0$ và $d_{2} : 4 x - 3 y + 12 = 0$ ...

Bài 1 trang 57 Toán 10 Tập 2: Lập phương trình tham số và phương trình tổng quát của đường thẳng d trong mỗi trường hợp sau...

Bài 2 trang 57 Toán 10 Tập 2: Cho tam giác ABC biết $A (2; 5), B (1; 2)$ và $C (5; 4)$ ...

Bài 3 trang 57 Toán 10 Tập 2: Lập phương trình tham số và phương trình tổng quát của đường thẳng $Δ$ trong mỗi trường hợp sau...

Bài 4 trang 57 Toán 10 Tập 2: Xét vị trí tương đối của cặp đường thẳng $d_{1}$ và $d_{2}$ sau đây...

Bài 5 trang 58 Toán 10 Tập 2: Cho đường thẳng d có phương trình tham số ${\begin{cases} x = 2 - t \\ y = 5 + 3 t \end{cases}$ ...

Bài 6 trang 58 Toán 10 Tập 2: Tìm số đo của góc giữa hai đường thẳng $d_{1}$ và $d_{2}$ trong các trường hợp sau...

Bài 7 trang 58 Toán 10 Tập 2: Tính khoảng cách từ điểm M đến đường thẳng $Δ$ trong các trường hợp sau...

Bài 8 trang 58 Toán 10 Tập 2: Tính khoảng cách giữa hai đường thẳng $Δ : 3 x + 4 y - 10 = 0$ và $Δ^{'} : 6 x + 8 y - 1 = 0$ ...

Bài 9 trang 58 Toán 10 Tập 2: Trong mặt phẳng Oxy cho điểm $S (x; y)$ di động trên đường thẳng $d : 12 x - 5 y + 16 = 0$ . Tính khoảng cách ngắn nhất từ điểm $M (5; 10)$ đến điểm S...

Bài 10 trang 58 Toán 10 Tập 2: Một người đang viết chương trình cho trò chơi đá bóng robot. Gọi $A (- 1; 1), B (9; 6), C (5; - 3)$ là 3 vị trí trên màn hình...

Từ khóa :

Giải bài tập Toán 10

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

298

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

319

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

347

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

295

Tìm kiếm

Bài Viết Xem Nhiều

Bài Viết Cùng Lớp

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

2021 © All Rights Reserved.