Toptailieu biên soạn và giới thiệu lời giải Toán 11 (Cánh diều) Bài 1: Phép tính lũy thừa với số mũ thực hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi SGK Toán 11 Bài 1 từ đó học tốt môn Toán 11.
Nội dung bài viết
Toán 11 (Cánh diều) Bài 1: Phép tính lũy thừa với số mũ thực
Giải Toán 11 trang 27 Tập 2
Lời giải:
– Những khái niệm lũy thừa với số mũ nguyên, số mũ hữu tỉ và số mũ thực của một số thực được xây dựng dựa trên lũy thừa bậc n của a, kí hiệu là an, là tích của n thừa số a:
an = a.a.a...a (n thừa số a) với n là số nguyên dương.
Số a được gọi là cơ số, n được gọi là số mũ.
– Tính chất của lũy thừa mà ta đã học ở các lớp dưới:
⦁ am . an = am+n;
⦁ aman=am−n;
⦁ (am)n=am.n;
⦁ (a . b)m = am . bm;
⦁ (ab)m=ambm;
⦁ Với a > 1 thì am > an ⇔ m > n;
⦁Với 0 < a < 1 thì am > an ⇔ m < n.
I. Phép tính lũy thừa với số mũ hữu tỷ
Hoạt động 1 trang 27 Toán 11 Tập 2:
a) Cho n là một số nguyên dương. Với a là số thực tùy ý, nêu định nghĩa lũy thừa bậc n của a.
b) Với a là số thực tùy ý khác 0, nêu quy ước xác định lũy thừa bậc 0 của a.
Lời giải:
a) Lũy thừa bậc n của a, kí hiệu là an, là tích của n thừa số a: an = a.a.a...a (n thừa số a) với n là số nguyên dương.
Số a được gọi là cơ số, n được gọi là số mũ.
b) Quy ước xác định lũy thừa bậc 0 của a (với a khác 0) là: a0 =1.
Giải Toán 11 trang 28 Tập 2
Lời giải:
Ta có:
M=(13)12⋅(127)−5+(0,4)−4⋅25−2⋅(132)−1.
=(13)12⋅275+(25)−4⋅1252⋅321
=1312⋅(33)5+(52)4⋅1(52)2⋅25
=1312⋅315+5424⋅154⋅25
=33+2=27+2=29.
Hoạt động 2 trang 28 Toán 11 Tập 2:
a) Với a là số thực không ân, nêu định nghĩa căn bậc hai của a.
b) Với a là số thực tùy ý, nêu định nghĩa căn bậc ba của a.
Lời giải:
a) Căn bậc hai của một số thực a không âm, kí hiệu là √a là số x sao cho x2 = a.
b) Căn bậc ba của một số a tùy ý, kí hiệu là 3√a là số x sao cho x3 = a.
Luyện tập 2 trang 28 Toán 11 Tập 2: Các số 2 và –2 có phải là căn bậc 6 của 64 hay không?
Lời giải:
Ta thấy: 26 = 64 và (–2)6 = 64
Do đó, 2 và –2 là căn bậc 6 của 64.
Giải Toán 11 trang 29 Tập 2
Hoạt động 3 trang 29 Toán 11 Tập 2:
a) Với mỗi số thực a, so sánh: √a2 và |a|; 3√a3 và a.
b) Cho a, b là hai số thực dương. So sánh √a⋅b và √a⋅√b.
Lời giải:
a) ⦁Ta có: 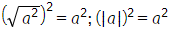
Do đó √a2 = |a|
⦁Ta có: (3√a3)3=a3; (a)3=a3, với mọi số thực a
Do đó 3√a3=a.
b) Với a, b là hai số thực dương, ta có: (√a⋅b)2=ab; (√a⋅√b)2=ab
Do đó √a⋅b=√a⋅√b.
Luyện tập 3 trang 29 Toán 11 Tập 2: Rút gọn mỗi biểu thức sau:
a) 3√12564.4√81; b) 5√98.5√3435√64.
Lời giải:
a) 3√12564⋅4√81=3√(54)3⋅4√34=54⋅3=154;
b) 5√98⋅5√3435√64=5√98⋅34364=5√2⋅72⋅7326=5√7525=5√(72)5=72.
Hoạt động 4 trang 29 Toán 11 Tập 2: Thực hiện các hoạt động sau:
a) So sánh 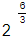
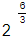
Lời giải:
a)Ta có: 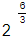
b) Ta có: 3√26=3√(22)3=22
Mà 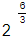
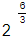
Giải Toán 11 trang 30 Tập 2
Luyện tập 4 trang 30 Toán 11 Tập 2: Rút gọn mỗi biểu thức: N=x43y+xy433√x+3√y(x>0,y>0).
Lời giải:
Với x > 0 và y > 0, ta có:
N=x43y+xy433√x+3√y=3√x4y+x3√y43√x+3√y
=3√x3⋅3√x⋅y+x⋅3√y3⋅3√y3√x+3√y
=3√x3⋅x⋅y+x⋅y⋅3√y3√x+3√y
=xy(3√x+3√y)3√x+3√y=xy.
II. Phép tính lũy thừa với số mũ thực
Hoạt động 5 trang 30 Toán 11 Tập 2: Xét số vô tỉ √2=1,414213562...
Nêu dự đoán về giá trị của số 3√2 (đến hàng phần trăm).
Lời giải:
Từ Bảng 1 ta thấy:
⦁r1 = 1 thì 3r1=3;
⦁r2 = 1,4 thì 3r2=4,655536722...≈4,66;
...
⦁r6 = 1,41421 thì 3r6=4,728785881...≈4,73;
…
Dự đoán: 3√2≈4,73.
Giải Toán 11 trang 31 Tập 2
Luyện tập 5 trang 31 Toán 11 Tập 2: So sánh 10√2 và 10.
Lời giải:
Vì 10√2≈25,95>10 nên 10√2>10.
Lời giải:
Tính chất của phép tính lũy thừa với số mũ nguyên của một số thực dương:
⦁ am . an = am+n;
⦁ aman=am−n;
⦁ (am)n=am⋅n;
⦁ (a . b)m = am . bm;
⦁ (ab)m=ambm;
⦁ Với a > 1 thì am > an ⇔ m > n;
⦁Với 0 < a < 1 thì am > an ⇔ m < n.
Giải Toán 11 trang 32 Tập 2
Luyện tập 6 trang 32 Toán 11 Tập 2: Không sử dụng máy tính cầm tay, hãy so sánh các số 22√3 và 23√2.
Lời giải:
Ta có: (2√3)2=12; (3√2)2=18
Vì 12 < 18, nên 2√3<3√2
Do cơ số 2 lớn hơn 1 nên 22√3<23√2.
Lời giải:
a) (−2,7)−4≈0,02;
b) (√3−1)3√4+1≈0,45.
Bài tập
Giải Toán 11 trang 33 Tập 2
Bài 1 trang 33 Toán 11 Tập 2: Tính:
Lời giải:
Ta có:
a) (1256)−0,75+(127)−43=(1256)−34+(127)−43
=25634+2743=4√2563+3√274
=4√(28)3+3√(33)4=4√224+3√312
=4√(26)4+3√(34)3=26+34=64+81=145.
b) (149)−1,5−(1256)−23=(149)−32−(1256)−23
=4932−25623=√493−3√2562
=√(72)3−3√(28)2=√76−3√216
=√(73)2−3√2⋅215=73−3√2⋅3√(25)3
=73−3√2⋅25=73−323√2.
c)
=(26+2√3−22√3−2)⋅2−2√3=26+2√3−2√3−22√3−2−2√3
=26−2−2=64−122=64−14=2554.
a) a13⋅√a; b) b12⋅b13⋅6√b; c) a43:3√a; d) 3√b:b16.
Lời giải:
a) a13⋅√a=a13.a12=a13+12=a56=6√a5;
b) b12⋅b13⋅6√b=b12⋅b13⋅b16=b12+13+16=b1;
c) a43:3√a=a43:a13=a43−13=a1;
d) 3√b:b16=b13:b16=b13−16=b16=6√b.
Bài 3 trang 33 Toán 11 Tập 2: Rút gọn mỗi biểu thức sau:
a) a73−a13a43−a13 (a>0;a≠1); b) 3√√a12b6(a>0,b>0).
Lời giải:
Ta có:
a) a73−a13a43−a13=a13(a2−1)a13(a−1)=(a−1)(a+1)a−1=a+1;
b) 3√√a12b6=3√(a12b6)12=(a12b6)12⋅13=(a12b6)16=a2b.
Bài 4 trang 33 Toán 11 Tập 2: Viết các số sau theo thứ tự tăng dần:
a) 11,5; 3−1; (12)−2; b) 20220; (45)−1; 512.
Lời giải:
a) Ta có: 11,5=132=√13=1; 3−1=13; (12)−2=22=4
Vì 13<1<4 nên 3−1<11,5<(12)−2.
b) Ta có: 20220=1; (45)−1=54; 512=√5>√4=2
Vì 1<54<2<√5 nên 20220<(45)−1<512.
Bài 5 trang 33 Toán 11 Tập 2: Không sử dụng máy tính cầm tay, hãy so sánh các số sau:
Lời giải:
a) Ta có 3 < 4 nên
Vì cơ số 6 lớn hơn 1 nên do đó
b) Ta có: 3 < 5 nên
Vì cơ số 0,2 thỏa mãn 0 < 0,2 < 1 nên
Lời giải:
Sao Hỏa quay quanh Mặt Trời thì mất số năm Trái Đất là:
.
Xem thêm Lời giải bài tập Toán 11 Cánh diều hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.