Toptailieu biên soạn và giới thiệu giải sách bài tập Toán 7 Bài 5: Làm quen với số thập phân vô hạn tuần hoànsách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập trong SBT Toán 7 Bài 5.
Nội dung bài viết
Giải SBT Toán 7 Bài 5(Kết nối tri thức): Làm quen với số thập phân vô hạn tuần hoàn
2160;−8125;28−63;37800
Lời giải:
*) 2160
Ta có:
2160=21:360:3=720.
Mẫu số: 20 = 2.2.5 nên 20 chỉ có ước nguyên tố là 2 và 5.
Do đó, phân số 720 hay 2160 viết được dưới dạng số thập phân hữu hạn.
*) −8125
Mẫu số 125 = 53 nên 125 chỉ có ước nguyên tố là 5.
Do đó, phân số −8125 viết được dưới dạng số thập phân hữu hạn.
*) 28−63
Ta có:
28−63=28:(−7)(−63):(−7)=−49
Mẫu số 9 = 3.3 nên 9 có ước nguyên tố là 3.
Do đó, phân số −49 hay 28−63 viết được dưới dạng số thập phân vô hạn tuần hoàn.
*) 37800
Mẫu số 800 = 25.52 nên 800 chỉ có ước nguyên tố là 2 và 5.
Do đó, phân số 37800viết được dưới dạng số thập phân hữu hạn.
Vậy phân số viết được thành số thập phân vô hạn tuấn hoàn là 28−63.
Bài 2.2 trang 24 sách bài tập Toán 7: Viết số thập phân 2,75 dưới dạng phân số tối giản.
Lời giải:
Ta có:
2,75 = 275100=275:25100:25=74.
Số thập phân 2,75 được viết dưới dạng phân số tối giản là 74
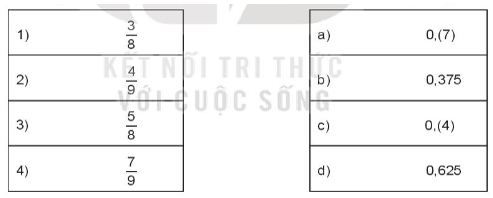 Lời giải:
Lời giải:
Ta có:
38=0,375
49=0,(4)
58=0,625
79=0,(7)
Ta có kết quả nối sau:
1 – b
2 – c
3 – d
4 – a
Lời giải:
1315 mẫu số là 15 có ước nguyên tố là 3 và 5 nên phân số được viết dưới dạng số thập phân vô hạn tuần hoàn.
134 mẫu số là 4 có ước nguyên tố là 2 nên phân số được viết dưới dạng số thập phân hữu hạn.
−118 mẫu số là 18 có ước nguyên tố là 3 và 2 nên phân số được viết dưới dạng số thập phân vô hạn tuần hoàn.
116 mẫu số là 6 có ước nguyên tố là 2 và 3 nên phân số được viết dưới dạng số thập phân vô hạn tuần hoàn.
720 mẫu số là 20 có ước nguyên tố là 2 và 5 nên phân số được viết dưới dạng số thập phân hữu hạn.
−1950 mẫu số là 50 có ước nguyên tố là 2 và 5 nên phân số được viết dưới dạng số thập phân hữu hạn.
Các phần tử của tập hợp A là 134; 720; −1950
Các phần tử của tập hợp B là 1315; 116; −118.
+ Ta đi so sánh các phần tử của tập hợp A.
−1950 là phân số âm và 134;720là phân số dương nên −1950 bé nhất.
Lại có 134 là phân số dương có tử số lớn hơn mẫu số nên 134 > 1
720 là phân số dương có tử số bé hơn mẫu số nên 720 < 1.
Tập hợp A gồn các phân số được viết thành số thập phân hữu hạn, khi liệt kê và viết các phần tử theo thứ tự từ bé đến lớn là:
A=(−1950;720;134)
+ Ta đi so sánh các phần tử của tập hợp B.
−118 là phân số âm và 1315; 116 là phân số dương nên −118 bé nhất.
Lại có 116 là phân số dương có tử số lớn hơn mẫu số nên 116 > 1
1315 là phân số dương có tử số bé hơn mẫu số nên 1315 < 1.
Tập hợp B gồm các phân số được viết thành số thập phân hữu hạn, khi liệt kê và viết các phần tử theo thứ tự từ bé đến lớn là:
B=(−118;1315;116)
Bài 2.5 trang 24 sách bài tập Toán 7: Viết số thập phân 3,(5) dưới dạng phân số.
Lời giải:
3,(5)=3+0,(5)=3+5.0,(1)=3+5.19=3+59=329
Lời giải:
Ta có:
17=0,(142857)
Chu kỳ phần thập phân có 6 chữ số.
Ta có: 105 : 6 = 17 dư 3.
Do đó, chữ số thập phân thứ 105 là 2.
Bài 2.7 trang 25 sách bài tập Toán 7: Kết quả của phép tính 1 : 1(3) bằng:
A. 0,(75);
B. 0,3;
C. 0,(3);
D. 0,75.
Hãy chọn câu trả lời đúng.
Lời giải:
1 : 1(3) = 1 : [1 + 0,(3)] = 1 : [1 + 3.0,(1)] = 1 : [1 + 3.19]
= 1 : [1 + 39] = 1 : 43 =34 = 0,74
Đáp án đúng là D
Bài 2.8 trang 25 sách bài tập Toán 7: Cho hai số a = 2,4798; b = 3,(8).
a) Gọi a’ và b’ lần lượt là kết quả làm tròn số a đến hàng phần mười và làm tròn số b với độ chính xác 0,5. Tính a’; b’ và so sánh a’ với a; b’ với b.
b) Sử dụng kết quả câu a) để giải thích kết luận sau đấy đúng:
2,4798 . 3,(8) = 10,2(3).
Lời giải:
a) Ta làm tròn số a = 2,4798 đến hàng phần mười ta được kết quả là a’ = 2,5.
Làm tròn số b với độ chính xác 0,5 nghĩa là làm tròn số b đến hàng đơn vị. Khi đó ta được kết quả là b’ = 4.
So sánh a’ với a ta thấy a’ lớn hơn a (2,5 > 2,4788)
So sán b’ với b ta thấy b’ lớn hơn b (4 > 3,(8))
Lời giải:
Số này là số thập phân vô hạn không tuần hoàn vì phần thập phân của số √2 cũng có phần thập phân vô hạn không tuần hoàn nên phần thập phân của số này cũng vô hạn không tuần hoàn.
Xem thêm các bài giải SBT Toán lớp 7 Kết nối với tri thức hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.