Toptailieu.vn giới thiệu Giải bài tập Toán lớp 10 Bài 1. Vẽ đồ thị hàm số bậc hai bằng phần mềm Geogebra sách Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10 Tập 2. Mời các bạn đón xem:
Nội dung bài viết
Toán 10 Chân trời sáng tạo Bài 2: Vẽ ba đường conic bằng phần mềm Geogebra
Thực hành 1 trang 92 Toán 10 Tập 2: Vẽ các elip sau
a) x210+y24=1
b) x212+y23=1
c) x2100+y236=1
Phương pháp giải:
Bước 1: Khởi động phần mềm Geogebra
Bước 2: Nhập phương trình elip x2a2+y2b2=1 theo cú pháp x^2/a^2 + y^2/b^2 = 1 vào vùng nhập lệnh
Bước 3: Quan sát hình vẽ xuất hiện trên vùng làm việc
Lời giải
Thực hiện các bước đã nêu ở phương pháp ta có
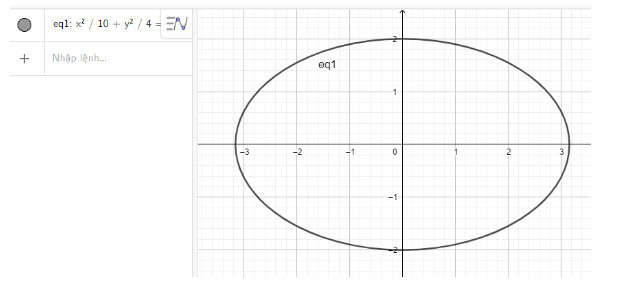
a) Nhập phương trình elip theo cú pháp x^2/10 + y^2/4 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:
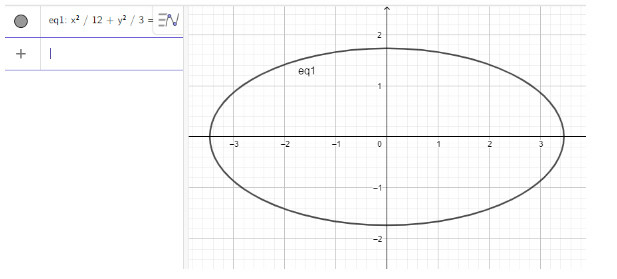
b) Nhập phương trình elip theo cú pháp x^2/12 + y^2/3 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:
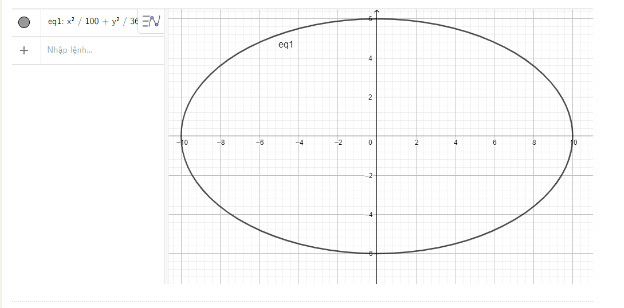
c) Nhập phương trình elip theo cú pháp x^2/100 + y^2/36 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:
Phương pháp giải:
Từ chiều rộng và chiều cao xác định a, b. Từ đó xác định công thức elip và hình dạng
Lời giải
Ta có: Chiều cao và chiều rộng của đường hầm là 4m, 10m nên ta có: a=5,b=4
Nên phương trình chính tắc của elip có dạng x225+y216=1
Nhập phương trình elip theo cú pháp x^2/25 + y^2/16 = 1 {y>=0} vào vùng nhập lệnh ta có hình vẽ mô phỏng đường hầm dưới đây
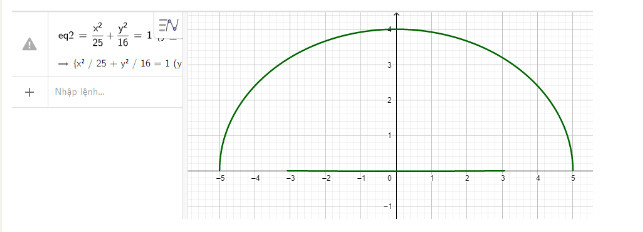
Vậy phương trình mô phỏng đường hầm là x225+y216=1 với y≥0
Và có hình mô phỏng thực tế như hình trên.
Thực hành 3 trang 94 Toán 10 Tập 2: Vẽ các hypebol sau:
a) x210−y26=1
b) x24−y23=1
c) x264−y236=1
Phương pháp giải
Bước 1: Khởi động phần mềm Geogebra
Bước 2: Nhập phương trình hypebol x2a2−y2b2=1 theo cú pháp
x^2/a^2 - y^2/b^2 = 1 vào vùng nhập lệnh
Bước 3: Quan sát hình vẽ xuất hiện trên vùng làm việc
Lời giải
Thực hiện các bước đã nêu ở phương pháp ta có
a) Nhập phương trình hypebol theo cú pháp x^2/10 - y^2/6 = 1 vào vùng nhập lệnh ta được hình hypebpl dưới đây:
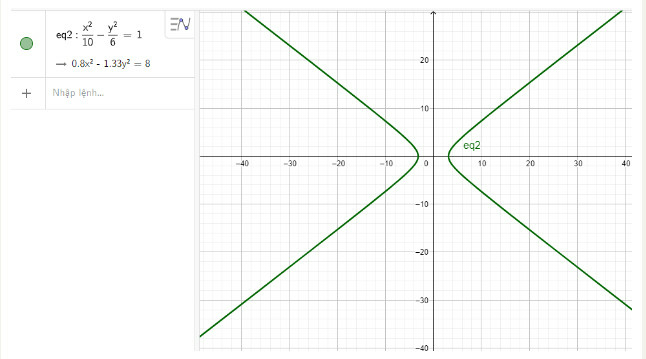
b) Nhập phương trình hypebol theo cú pháp x^2/4 - y^2/3 = 1 vào vùng nhập lệnh ta được hình hypebol dưới đây:
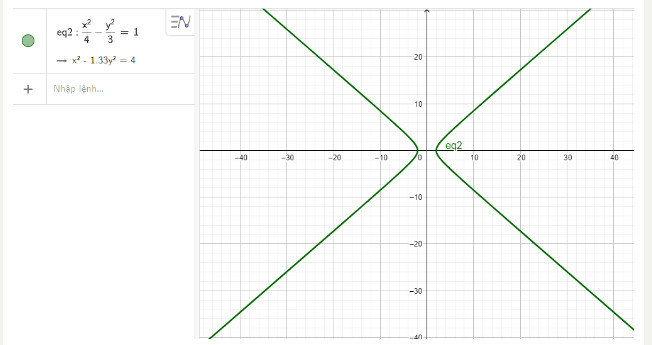
c) Nhập phương trình hypebol theo cú pháp x^2/64 - y^2/36 = 1 vào vùng nhập lệnh ta được hình hypebol dưới đây:
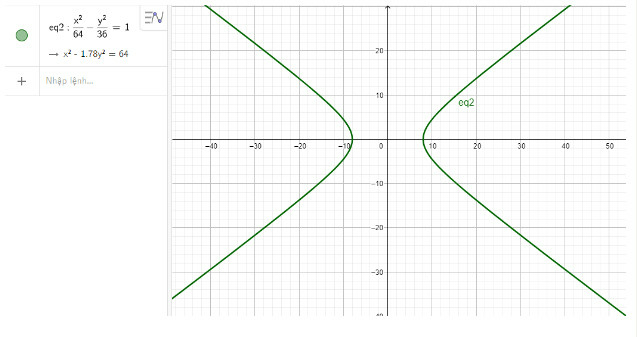
Thực hành 4 trang 96 Toán 10 Tập 2: Vẽ các parabol sau:
a) y2=16x
b) y2=x
c) y2=32x
Phương pháp giải:
Bước 1: Khởi động phần mềm Geogebra
Bước 2: Nhập phương trình parabol y2=2px theo cú pháp y^2 = 2px vào vùng nhập lệnh
Bước 3: Quan sát hình vẽ xuất hiện trên vùng làm việc
Lời giải
Thực hiện các bước đã nêu ở phương pháp ta có
a) Nhập phương trình parabol theo cú pháp y^2 = 16x vào vùng nhập lệnh ta được hình parabol dưới đây:
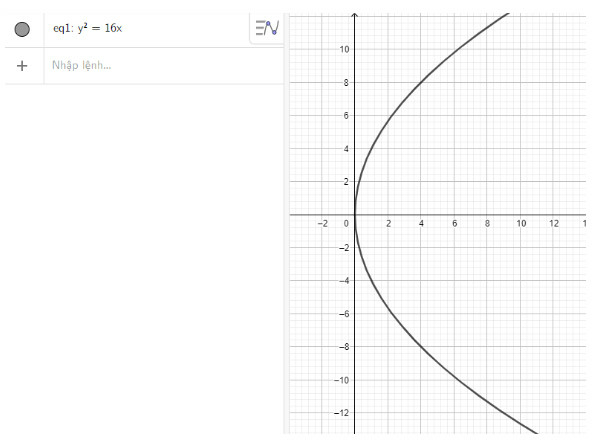
b) Nhập phương trình parabol theo cú pháp y^2 = x vào vùng nhập lệnh ta được hình parabol dưới đây:
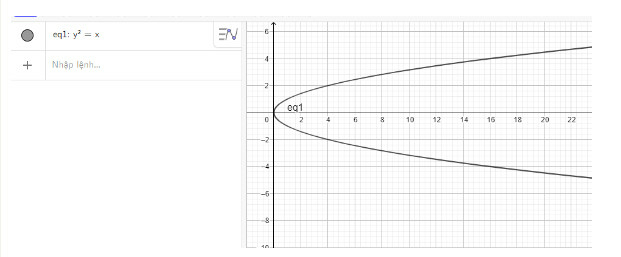
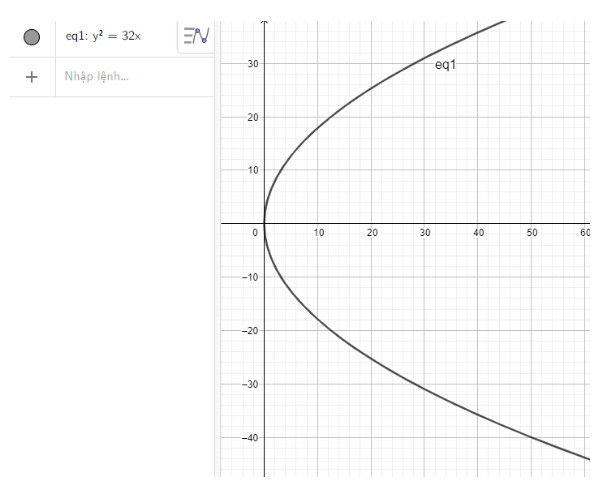
c) Nhập phương trình parabol theo cú pháp y^2 = 32x vào vùng nhập lệnh ta được hình parabol dưới đây:
Nội dung bài viết
Phương pháp giải:
Bước 1: Giả sử phương trình của parabol
Bước 2: Từ kích thước giả thiết cho, xác định điểm nằm trên phương trình
Bước 3: Xác định phương trình parabol
Bước 4: Sử dụng Geogebra vẽ hình dạng mô phỏng chóa đèn
Lời giải
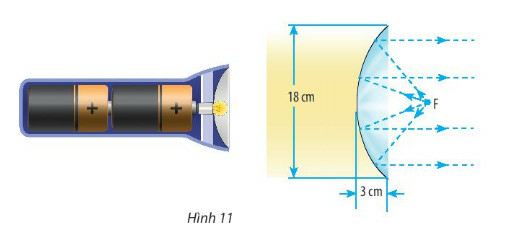
Chóa đèn có hình dạng parabol nên phương trình mô phỏng chóa đèn có dạng y2=2px
Gắn hệ tọa độ Oxy vào chóa đèn với gốc tọa độ tại đỉnh chóa đèn, suy ta phương trình đó đi qua điểm có tọa độ (3; 9)
Thay tọa độ điểm (3; 9) vào phương trình y2=2px, ta có 92=2p.3⇒p=272
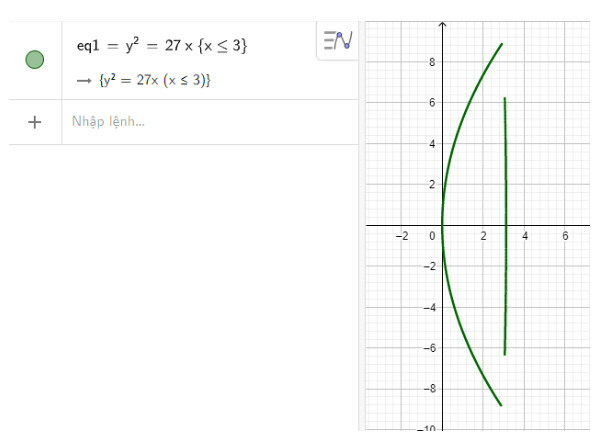
Suy ra phương trình mô tả chóa đèn là y2=27x với x≤3
Hình ảnh mô phỏng chóa đèn có dạng như hình dưới:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.