Toptailieu biên soạn và giới thiệu giải sách bài tập Toán 7 Bài 10: Tiên đề Eculid. Tính chất của hai đường thẳng song song sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập trong SBT Toán 7 Bài 10.

Giải SBT Toán 7 Bài 10 (Kết nối tri thức): Tiên đề Eculid. Tính chất của hai đường thẳng song song

Bài 3.18 trang 42 sách bài tập Toán 7: Cho Hình 3.19, biết a // b.Tính số đo góc A1.

b) So sánh góc A4 và B2.

c) Tính số đo góc A2.

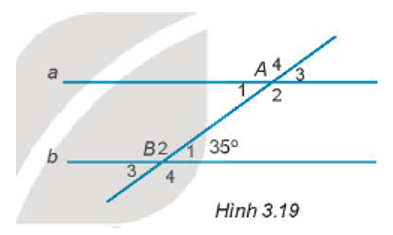Lời giải:

a) Vì a // b nên ${\hat{A}}_1$ và góc ${\hat{B}}_1$ là hai góc so le trong.

Do đó, ${\hat{A}}_1$ = ${\hat{B}}_1$ = 35o.

b) Vì a // b nên các cặp góc so le trong bằng nhau và các cặp góc đồng vị bằng nhau.

Ta có, ${\hat{A}}_4$ và ${\hat{B}}_2$ là hai góc đồng vị.

Do đó, ${\hat{A}}_4$ = ${\hat{B}}_2$.

c) Vì ${\hat{A}}_1$ và ${\hat{A}}_2$ là hai góc kề bù nên ${\hat{A}}_1$ + ${\hat{A}}_2$ = 180o

Thay số: 35o + ${\hat{A}}_2$ = 180o

${\hat{A}}_2$ = 180o – 35o

${\hat{A}}_2$ = 145o.

Bài 3.19 trang 42 sách bài tập Toán 7: Vẽ lại Hình 3.20 vào vở: a) Giải thích tại sao Ax // By.

b) Tính số đo góc ABy’.

c) Tính số đo góc ABM.

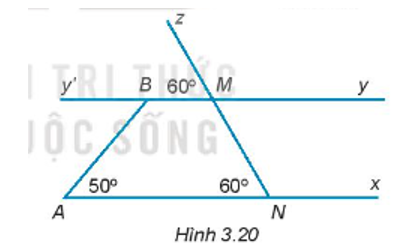
Lời giải:

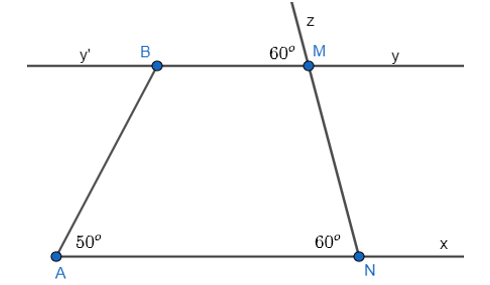
a) Ta có:

$\widehat{zMy}\text{'}$ = $\widehat{zNA}$ = $60°$ mà $\widehat{zMy\text{'}}$ và $\widehat{zNA}$ là hai góc đồng vị.

Do đó, Ax // By.

 b) Vì Ax // By nên các góc so le trong bằng nhau và các góc đồng vị bằng nhau.

Lại có: $\widehat{ABy\text{'}}$ và $\widehat{BAx}$ là hai góc so le trong.

Do đó, $\widehat{ABy\text{'}}$ = $\widehat{BAx}$ = 50^o.

c) Vì $\widehat{ABy\text{'}}$ và $\widehat{ABM}$ là hai góc kề bù nên:

 $\widehat{ABy\text{'}}$ + $\widehat{ABM}$ = 180^o

Thay số: 50^o + $\widehat{ABM}$ = 180^o

$\widehat{ABM}$ = 180^o – 50^o

$\widehat{ABM}$ = 130^o.

Bài 3.20 trang 42 sách bài tập Toán 7: Trong các phát biểu sau, phát biểu nào diễn đạt đúng nội dung của tiên đề Euclid?

a) Qua điểm A nằm ngoài đường thẳng d có ít nhất một đường thẳng song song với d.

b) Nếu qua điểm A nằm ngoài đường thẳng d có hai đường thẳng song song với d thì chúng trùng nhau.

c) Có duy nhất một đường thẳng song song với một đường thẳng cho trước.

d) Cho điểm A nằm ngoài đường thẳng d. Đường thẳng đi qua A và song song với đường thẳng d là duy nhất.

Lời giải:

Phát biểu diễn đạt đúng nội dung tiên đề Euclid là phát biểu b và phát biểu d.

Bài 3.21 trang 43 sách bài tập Toán 7: Cho đường thẳng xx’, điểm A thuộc xx’. Trên tia Ax’ lấy điểm B (điểm B khác điểm A). Vẽ tia By, trên tia By lấy điểm M. Hai điểm N và P thảo mãn: $\widehat{NMA}$ = $\widehat{MAB}$; $\widehat{PMy}= \widehat{MBx\text{'}}$(H.3.21) Giải thích tại sao ba điểm N; M; P thẳng hàng.

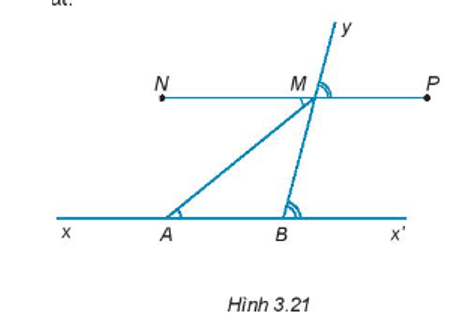Lời giải:

Theo đề bài ra ta có:

$\widehat{NMA}= \widehat{MAB}$, mà hai góc này ở vị trí so le trong, suy ra MN // xx;

$\widehat{PMy}=\widehat{MBx\text{'}}$, mà hai góc này ở vị trí đồng vị, suy ra MP // xx’

Theo tiên đề Euclid, qu điểm M chỉ có một đường thẳng song song với xx’. Mà MN và NP cùng song song với xx’ nên MN vag MP trùng nhau.

Do đó, ba điểm M, N, P thẳng hàng.

Bài 3.22 trang 43 sách bài tập Toán 7: Vẽ lại Hình 3.22 vào vở: a) Giải thích tại sao a//b

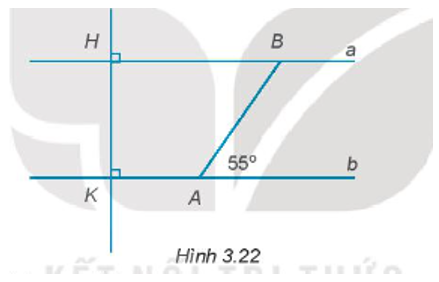
a) Giải thích tại sao a // b.

b) Tính số đo góc ABH.

Lời giải:

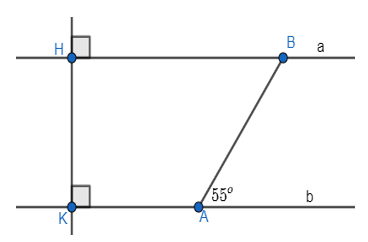a) Vì HK vuông góc với a tại H; HK vuông góc với b tại K nên a // b (quan hệ từ vuông góc đến song song).

b) Vì a // b nên các góc so le trong bằng nhau và các góc đồng vị bằng nhau.

Lại có: $\widehat{ABH}$ và $\widehat{BAb}$ là hai góc so le trong.

Do đó, $\widehat{ABH}= \widehat{BAb}$ = 55o.

Bài 3.23 trang 43 sách bài tập Toán 7: Vẽ lại Hình 3.23 vào vở. Giải thích tại sao: a) xx’ // yy’.

b) xx’ a.

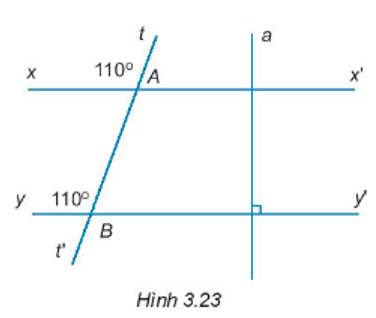Lời giải:

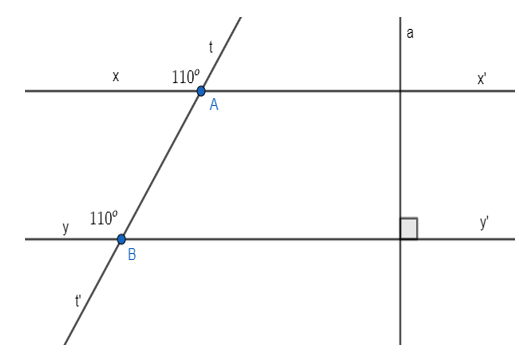a) Ta có: $\widehat{tAx}$ = 110o và $\widehat{yBt}$ = 110o nên $\widehat{tAx}$ = $\widehat{yBt}$ = 110o. Mà hai góc này ở vị trí đồng vị. Do đó, xx’ song song với yy’.

b) Vì a vuông góc với yy’ mà yy’ lại song song với xx’ nên a vuông góc với xx’.

Bài 3.24 trang 44 sách bài tập Toán 7: Cho Hình 3.24. a) Giải thích tại sao yy’ // zz’.

b) Tính số đo góc ABz.

c) Vẽ tia phân giác At của góc MAB, tia At cắt đường thẳng zz’ tại H. Tính số đo góc AHN.

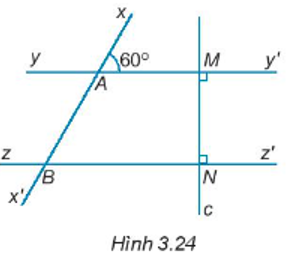Lời giải:

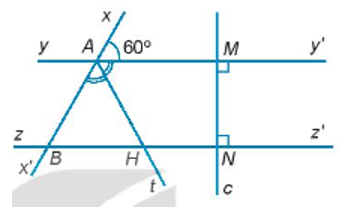a) Theo hình vẽ ta có:

MN$\perp$yy’ và MN $\perp$ zz’ nên yy’ // zz’.

b) Ta có:

$\widehat{xAy\text{'}}$ và $\widehat{ABz\text{'}}$ là hai góc đồng vị, mà yy’ // zz’ nên $\widehat{xAy\text{'}}$ = $\widehat{ABz\text{'}}$ = 60o.

Lại có $\widehat{ABz\text{'}}$ và $\widehat{ABz}$ là hai góc kề bù.

Do đó, $\widehat{ABz\text{'}}$ + $\widehat{ABz}$ = 180o.

Thay số: 60o + $\widehat{ABz}$ = 180o.

$\widehat{ABz}$ = 180o – 60o

$\widehat{ABz}$ = 120o.

c) Vì yy’ // zz’ mà hai góc $\widehat{ABz}$ và $\widehat{MAB}$ là hai góc so le trong nên $\widehat{ABz}$ = $\widehat{MAB}$ = 120o.

Vì At là tia phân giác của góc $\widehat{MAB}$ nên $\widehat{HAM}$ = $\widehat{HAB}=\frac{\widehat{MAB}}{2}=\frac{120°}{2}=60°$

Vì yy’ // xx’ và  $\widehat{HAM}$; $\widehat{AHB}$ là hai góc so le trong nên $\widehat{HAM}=\widehat{AHB}$ = 60o.

Lại có: $\widehat{AHB}$ và $\widehat{AHN}$ là hai góc kề bù nên $\widehat{AHB }+\widehat{AHN}$ = 180o.

Thay số: 60o + $\widehat{AHN}$= 180o

 $\widehat{AHN}$= 180o – 60o

$\widehat{AHN}$ = 120o.

Bài 3.25 trang 44 sách bài tập Toán 7: Cho Hình 3.25: a) Giải thích tại sao Ax // By.

b) Tính số đo ACB.

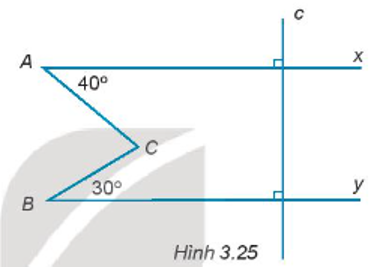Lời giải:

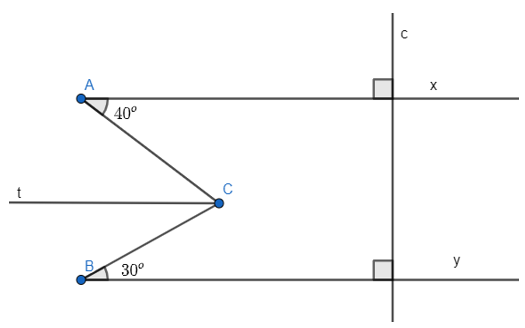a) Vì Ax $\perp$ c; By $\perp$ c nên Ax // By.

b) Kẻ Ct song song với Ax nên Ct cũng song song với By.

Vì Ct // Ax và $\widehat{xAC}$ và $\widehat{ACt}$ là hai góc so le trong nên $\widehat{xAC}$ = $\widehat{ACt}$ = 40o.

Vì Ct // By và $\widehat{BCt}$ và $\widehat{yBC}$ là hai góc so le trong nên $\widehat{BCt}$ = $\widehat{yBC}$ = 30o.

Lại có: $\widehat{ABC}$ = $\widehat{ACt}$ + $\widehat{BCt}$ = 40o + 30o = 70o.

Vậy $\widehat{ABC}$ = 70o.

Bài 3.26 trang 44 sách bài tập Toán 7: Cho Hình 3.26, biết Ax // Dy. $\widehat{xAC}=50°$; $\widehat{ACD}=110°$. Tính số đo $\widehat{CDy}$.

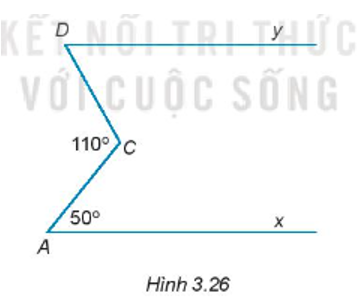Lời giải:

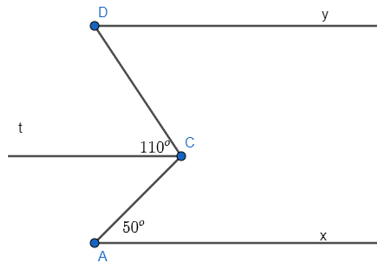
Kẻ tia Ct song song với Ax nên Ct song song với Dy (do Ax // Dy)

Vì Ax // Ct và $\widehat{CAx}$ và $\widehat{ACt}$ là hai góc so le trong nên $\widehat{CAx}$ = $\widehat{ACt}$ = 50o.

Ta lại có:

$\widehat{ACt}$ + $\widehat{tCD}$ = 110o

50o + $\widehat{tCD}$ = 110o

$\widehat{tCD}$ =110o – 50o

$\widehat{tCD}$ = 60o

Vì Ct // By và $\widehat{tCD}$ và $\widehat{CDy}$ là hai góc so le trong nên $\widehat{tCD}$ = $\widehat{CDy}$ = 60o.

Vậy $\widehat{CDy}$ = 60o.

Xem thêm các bài giải SBT Toán lớp 7 Kết nối với tri thức hay, chi tiết khác:

Bài 9: Hai đường thẳng song song và dấu hiệu nhận biết 

Bài 11: Định lí và chứng minh định lí

Ôn tập chương III 

Bài 12: Tổng các góc trong một tam giác

Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác