Toptailieu.vn giới thiệu Giải bài tập Toán lớp 7 trang 63, 64, 65, 66, 67 Bài 13. Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác sách Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7 Tập 1. Mời các bạn đón xem:
Giải SGK Toán 7 Bài 13 Kết nối tri thức: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác
1. Hai tam giác bằng nhau
Hoạt động 1 trang 63 SGK Toán 7 Tập 1: Gấp đôi một tờ giấy rồi cắt như Hình 4.9.
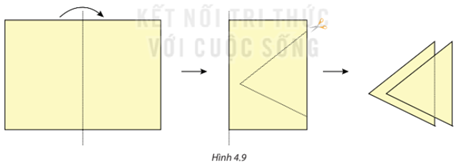
Phần được cắt ra là hai tam giác “chồng khít" lên nhau.
Theo em:
- Các cạnh tương ứng có bằng nhau không?
- Các góc tương ứng có bằng nhau không?
Phương pháp giải:
Quan sát hình 4.9 và trả lời câu hỏi.
Lời giải:
Quan sát hình vẽ ta thấy:
- Các cạnh tương ứng bằng nhau.
- Các góc tương ứng bằng nhau.
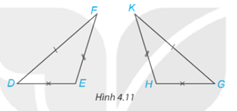
Phương pháp giải:
Quan sát hình 4.11 và trả lời câu hỏi.
Lời giải:
Ta có: Các cặp góc tương ứng là:
Các cặp cạnh tương ứng là:
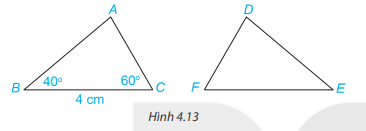
Phương pháp giải:
2 tam giác bằng nhau có các cặp cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau
Tổng số đo 3 góc trong 1 tam giác là 180 độ
Lời giải:
Vì nên BC = EF ( 2 cạnh tương ứng); ( 2 góc tương ứng)
Mà BC = 4 cm nên EF = 4 cm
Trong tam giác ABC có: ( định lí tổng ba góc trong một tam giác)
Mà nên
2. Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh (c.c.c)
Hoạt động 2 trang 65 SGK Toán 7 Tập 1: Vẽ tam giác ABC có , theo các bước sau:
- Dùng thước thẳng có vạch chia vẽ đoạn thẳng .
- Vẽ cung tròn tâm bán kính và cung tròn tâm bán kính sao cho hai cung tròn cắt nhau tại điểm .
- Vẽ các đoạn thẳng A B, A C ta được tam giác ABC.
Phương pháp giải:
Vẽ hình theo các bước hướng dẫn.
Lời giải:
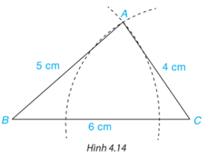
Hoạt động 3 trang 66 SGK Toán 7 Tập 1: Tương tự, vẽ thêm tam giác có .
- Dùng thước đo góc kiểm tra xem các góc tương ứng của hai tam giác A B C và có bằng nhau không.
- Hai tam giác A B C và có bằng nhau không?
Phương pháp giải:
- Đo các góc của hai tam giác và kết luận.
- Quan sát và chồng hai tam giác vừa vẽ lên nhau xem có bằng nhau k và kết luận.
Lời giải:
Các góc tương ứng của hai tam giác A B C và có bằng nhau.
Hai tam giác A B C và có bằng nhau
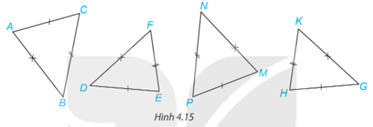
Câu hỏi trang 66 SGK Toán 7 Tập 1: Trong Hình 4.15, những cặp tam giác nào bằng nhau?
Phương pháp giải:
Quan sát nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
Lời giải:
Xét và có:
Vậy =(c.c.c)
Xét và có:
Vậy = (c.c.c)
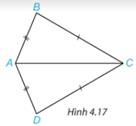
Luyện tập 2 trang 66 SGK Toán 7 Tập 1: Cho hình 4.17, biết AB=AD, BC=DC. Chứng minh rằng
Phương pháp giải:
Quan sát nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
Lời giải:
Xét tam giác và có:
Suy ra (c.c.c)
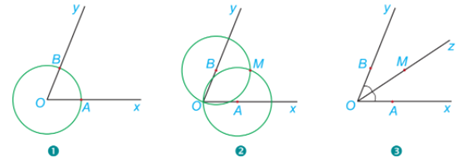
1.Vẽ đường tròn tâm O, cắt Ox và Oy lần lượt tại A và B.
2.Vẽ đường tròn tâm A bán kính AO và đường tròn tâm B bán kính BO. Hai đường tròn cắt nhau tại điểm M khác điểm O.
3. Vē tia Oz đi qua M.
Em hãy giải thích vì sao tia OM là tia phân giác của góc xOy.
Phương pháp giải:
Chứng minh hai tam giác và bằng nhau
Từ đó suy ra OM là tia phân giác của góc xOy.
Lời giải:
Xét và có:
OM chung
AM=BM (do hai đường tròn tâm A và B có bán kính bằng nhau)
= (c.c.c)
(hai góc tương ứng)
Mà tia OM nằm trong góc xOy
Vậy OM là tia phân giác của góc xOy.
Bài tập
(1)
(2)
(3)
(4)
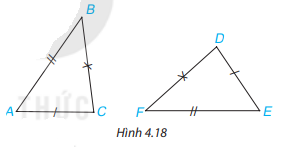
Phương pháp giải
Quan sát hình vẽ chỉ ra các cặp cạnh bằng nhau từ đó suy ra thứ tự đỉnh của hai tam giác bằng nhau.
Lời giải
Xét tam giác và có:
Suy ra (c.c.c)
Vậy khẳng định (2) đúng.
Bài 4.5 trang 67 SGK Toán 7 tập 1: Trong Hình 4.19, hãy chỉ ra hai cặp tam giác bằng nhau.
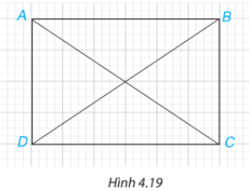
Phương pháp giải
Chỉ ra hai cặp tam giác có độ dài ba cặp cạnh bằng nhau.
Lời giải
+) Xét và có:
AB=CD
DB chung
BC=AD
=(c.c.c)
+) Xét và có:
AB=CD
DB chung
AD=CB
=(c.c.c)
Bài 4.6 trang 67 SGK Toán 7 tập 1: Cho Hình 4.20, biết
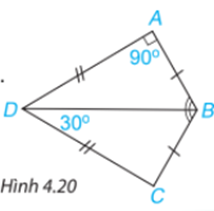
a) Chứng minh rằng .
b) Tính .
Phương pháp giải
a)Chứng minh ba cặp cạnh của hai tam giác bằng nhau.
b)
Lời giải
a) Xét và có:
DA=DC(gt)
BD chung
BA=BC
Vậy (c.c.c)
b) Ta có (hai góc tương ứng)
Mà nên ( 2 góc tương ứng)
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.