Toptailieu.vn giới thiệu Giải bài tập Toán lớp 7 trang 74 Luyện tập chung sách Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7 Tập 1. Mời các bạn đón xem:
Nội dung bài viết
Giải SGK Toán 7 Kết nối tri thức: Luyện tập chung
Bài tập
Phương pháp giải
Chứng minh hai tam giác bằng nhau theo trường hợp cạnh – góc - cạnh
Từ đó suy ra các cặp cạnh và các cặp góc tương ứng bằng nhau
Lời giải
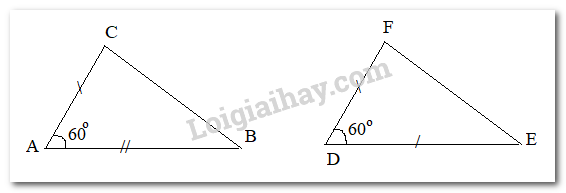
Xét hai tam giác ABC và DEF có:
AB=DEAC=DF^BAC=^EDF=60∘
⇒ΔABC=ΔDEF(c.g.c)
Do đó:
EF=BC=6cm
^DEF=^ABC=45o
^BAC+^ABC+^ACB=180o⇒60o+45o+^ACB=180o⇒^ACB=75o
⇒^EFD=^ACB=75o
Tính độ dài cạnh DF.
Phương pháp giải
Chứng minh hai tam giác bằng nhau theo trường hợp góc – cạnh – góc.
Lời giải
Xét hai tam giác ABC và DEF có:
^ABC=^DEF(=70∘)AB=DE^BAC=^EDF(=60∘)
⇒ΔABC=ΔDEF(g.c.g)
⇒DF=AC (2 cạnh tương ứng)
Mà AC = 6 cm
⇒DF=6cm
Bài 4.18 trang 74 SGK Toán 7 tập 1: Cho Hình 4.44, biết EC=ED và ^AEC=^AED. Chứng minh rằng:
a)ΔAEC=ΔAED;b)ΔABC=ΔABD.
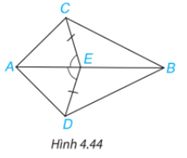
Phương pháp giải
Chứng minh hai tam giác bằng nhau theo trường hợp cạnh – góc - cạnh.
Lời giải
a)Xét hai tam giác AEC và AED có
EC=ED
^CEA=^DEA
AE chung
⇒ΔAEC=ΔAED(c.g.c)
b)
Do ΔAEC=ΔAED nên ^CAE=^DAE ( 2 góc tương ứng) và AC=AD ( 2 cạnh tương ứng).
Xét ΔABC và ΔABD có:
AB chung
^CAE=^DAE
AC=AD
⇒ΔABC=ΔABD(c.g.c)
a) Chứng minh rằng ΔOAC=ΔOBC.
b) Lấy điểm M trên tia đối của tia CO. Chứng minh rằng ΔMAC=ΔMBC.
Phương pháp giải
a) Chứng minh hai tam giác bằng nhau theo trường hợp góc – cạnh – góc.
b) Chứng minh hai tam giác bằng nhau theo trường hợp cạnh – góc - cạnh.
Lời giải
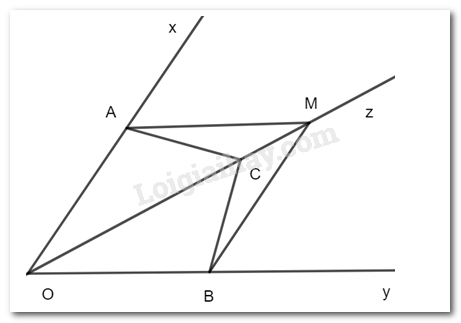
a)
Xét ΔOAC và ΔOBC có:
^AOC=^AOB(Oz là phân giác góc xOy)
OC chung
^CAO=^CBO.
⇒ΔOAC=ΔOBC(g.c.g)
b) Do ΔOAC=ΔOBC nên AC=BC ( 2 cạnh tương ứng)
Vì ^ACO và ^ACM kề bù
^BCO và ^BCM kề bù
Mà ^ACO=^BCO nên ^ACM=^BCM
Xét ΔMAC và ΔMBC có:
AC=BC
^ACM=^BCM
CM chung
⇒ΔMAC=ΔMBC(c.g.c)
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.