Lời giải:

Đáp án: C. v và t là hai đại lượng tỉ lệ nghịch với hệ số tỉ lệ 135.

Bài 78 trang 65 sách bài tập Toán 7: Viết mỗi số sau dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn:

${\displaystyle \frac{1}{3}};{\displaystyle \frac{17}{6}};{\displaystyle \frac{3}{4}};{\displaystyle \frac{-14}{11}};{\displaystyle \frac{-4}{55}}$.

Lời giải:

$\begin{array}{l}{\displaystyle \frac{1}{3}}=1:3==0,\mathrm{33333...}=0,(3);\\ {\displaystyle \frac{17}{6}}=17:6=2,\mathrm{83333...}=2,8(3);\\ {\displaystyle \frac{3}{4}}=3:4=0,75;\\ {\displaystyle \frac{-14}{11}}=-14:11==-1,\mathrm{272727...}=-1,(27);\\ {\displaystyle \frac{-4}{55}}=-4:55=-0,\mathrm{0727272...}=-0,0(72).\end{array}$

Bài 79 trang 65 sách bài tập Toán 7: Trong các số sau, số nào là số vô tỉ:

$34,(3);5,\mathrm{234561213141516...};-45,8(89);-\sqrt{121};\sqrt{19};\sqrt{{\displaystyle \frac{25}{16}}}$.

Lời giải:

Ta có: $-\sqrt{121}=-11;\sqrt{19}=4,\mathrm{35889894...};\sqrt{{\displaystyle \frac{25}{16}}}={\displaystyle \frac{5}{4}}=1,25$.

Vậy trong các số đã cho, số vô tỉ là: $5,\mathrm{234561213141516...};\sqrt{19}$.

Bài 80 trang 65 sách bài tập Toán 7: So sánh:

a) $213,6(42)$ và $213,\mathrm{598...}$;                                                    b) $-43,001$ và $-43,(001)$;

c) $-\sqrt{237}$ và $-15$;                                                                d) $\sqrt{1{\displaystyle \frac{40}{81}}}$ và $\sqrt{1{\displaystyle \frac{20}{101}}}$;

e) $2+\sqrt{37}$ và $6+\sqrt{2}$;                                                           g) ${\displaystyle \frac{\sqrt{5^2}+\sqrt{{15}^2}}{\sqrt{4^2}+\sqrt{{36}^2}}}$ và ${\displaystyle \frac{1}{\sqrt{2^2}}}$.

Lời giải:

a) $213,6(42)$ và $213,\mathrm{598...}$;

Ta có: $6>5$ nên $213,6(42)$ > $213,\mathrm{598...}$

b) $-43,001$ > $-43,(001)$;

c) $-\sqrt{237}$ và $-15$;

Ta có: $-\sqrt{237}=-16,\mathrm{52271164...}$.

Vậy $-\sqrt{237}$ < $-15$.                                     

d) $\sqrt{1{\displaystyle \frac{40}{81}}}$ và $\sqrt{1{\displaystyle \frac{20}{101}}}$;

Ta có:

$\sqrt{1{\displaystyle \frac{40}{81}}}=\sqrt{{\displaystyle \frac{121}{81}}}$

$\sqrt{1{\displaystyle \frac{20}{101}}}=\sqrt{{\displaystyle \frac{121}{101}}}$

Ta thấy: ${\displaystyle \frac{121}{81}}>{\displaystyle \frac{121}{101}}\to \sqrt{{\displaystyle \frac{121}{81}}}>\sqrt{{\displaystyle \frac{121}{101}}}$.

Vậy $\sqrt{1{\displaystyle \frac{40}{81}}}$ > $\sqrt{1{\displaystyle \frac{20}{101}}}$.

e) $2+\sqrt{37}$ và $6+\sqrt{2}$;

Ta có:

$2+\sqrt{37}=\sqrt{4}+\sqrt{37}$

$6+\sqrt{2}=\sqrt{36}+\sqrt{2}$                            

Ta thấy: $\begin{array}{l}\{\begin{array}{l}37>36\to \sqrt{37}>\sqrt{36}\\ 4>2\to \sqrt{4}>\sqrt{2}\end{array}\\ \Rightarrow \sqrt{37}+\sqrt{4}>\sqrt{36}+\sqrt{2}\end{array}$ hay $2+\sqrt{37}>6+\sqrt{2}$.

g) ${\displaystyle \frac{\sqrt{5^2}+\sqrt{{15}^2}}{\sqrt{4^2}+\sqrt{{36}^2}}}$ và ${\displaystyle \frac{1}{\sqrt{2^2}}}$.

Ta có:

${\displaystyle \frac{\sqrt{5^2}+\sqrt{{15}^2}}{\sqrt{4^2}+\sqrt{{36}^2}}}={\displaystyle \frac{5+15}{4+36}}={\displaystyle \frac{20}{40}}={\displaystyle \frac{2}{4}}={\displaystyle \frac{1}{2}}$.

${\displaystyle \frac{1}{\sqrt{2^2}}}={\displaystyle \frac{1}{2}}$.

Mà ${\displaystyle \frac{1}{2}}={\displaystyle \frac{1}{2}}$ suy ra: ${\displaystyle \frac{\sqrt{5^2}+\sqrt{{15}^2}}{\sqrt{4^2}+\sqrt{{36}^2}}}$ = ${\displaystyle \frac{1}{\sqrt{2^2}}}$.

Bài 81 trang 65 sách bài tập Toán 7: Sắp xếp các số sau theo thứ tự tăng dần:

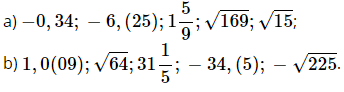
Lời giải:

a) $-0,34;-6,(25);1{\displaystyle \frac{5}{9}};\sqrt{169};\sqrt{15}$

Ta có:

$-0,34;-6,(25)<0<1{\displaystyle \frac{5}{9}};\sqrt{169};\sqrt{15}$.

Xét: $-0,34;-6,(25)\to -6,(25)<-0,34$.

Xét:

     $\begin{array}{l}1{\displaystyle \frac{5}{9}};\sqrt{169};\sqrt{15}:\\ 1{\displaystyle \frac{5}{9}}={\displaystyle \frac{14}{9}}=1,(5);\\ \sqrt{169}=13;\\ \sqrt{15}=3,\mathrm{8729833...}\\ \Rightarrow 1{\displaystyle \frac{5}{9}}<\sqrt{15}<\sqrt{169}\end{array}$

Vậy các số sắp xếp theo thứ tự tăng dần là: $-6,(25);-0,34;1{\displaystyle \frac{5}{9}};\sqrt{15};\sqrt{169}$.

b) $1,0(09);\sqrt{64};31{\displaystyle \frac{1}{5}};-34,(5);-\sqrt{225}$

Ta có:

$-34,(5);-\sqrt{225}<0<1,0(09);\sqrt{64};31{\displaystyle \frac{1}{5}};$

Xét $-34,(5);-\sqrt{225}=-15\to -34,(5)<-\sqrt{225}$

Xét

     $\begin{array}{l}1,0(09);\sqrt{64};31{\displaystyle \frac{1}{5}}:\\ \sqrt{64}=8\\ 31{\displaystyle \frac{1}{5}}={\displaystyle \frac{156}{5}}=31,2\\ \Rightarrow 1,0(09)<\sqrt{64}<31{\displaystyle \frac{1}{5}}\end{array}$

Vậy các số sắp xếp theo thứ tự tăng dần là: $-34,(5);-\sqrt{225};1,0(09);\sqrt{64};31{\displaystyle \frac{1}{5}}$. 

Bài 82 trang 65 sách bài tập Toán 7: Sắp xếp các số sau theo thứ tự giảm dần:

a) $2{\displaystyle \frac{1}{4}};\sqrt{16};-\sqrt{83};-\sqrt{196};-0,0(51)$;

b) $21{\displaystyle \frac{1}{6}};\sqrt{49};-\sqrt{144};-614,1;-111,0(3)$.

Lời giải:

a) $2{\displaystyle \frac{1}{4}};\sqrt{16};-\sqrt{83};-\sqrt{196};-0,0(51)$;

Ta có: $2{\displaystyle \frac{1}{4}};\sqrt{16}>0>-\sqrt{83};-\sqrt{196};-0,0(51)$.

Xét:

     $\begin{array}{l}2{\displaystyle \frac{1}{4}};\sqrt{16}:\\ 2{\displaystyle \frac{1}{4}}={\displaystyle \frac{9}{4}}=2,25\\ \sqrt{16}=4\\ \to \sqrt{16}>2{\displaystyle \frac{1}{4}}\end{array}$

Xét

     $\begin{array}{l}-\sqrt{83};-\sqrt{196};-0,0(51):\\ -\sqrt{83}=-9,\mathrm{1104335...}\\ -\sqrt{196}=-14\\ \Rightarrow -0,0(51)>-\sqrt{83}>-\sqrt{196}\end{array}$

Vậy các số sắp xếp theo thứ tự giảm dần là: $\sqrt{16};2{\displaystyle \frac{1}{4}};-0,0(51);-\sqrt{83};-\sqrt{196}$.

b) $21{\displaystyle \frac{1}{6}};\sqrt{49};-\sqrt{144};-614,1;-111,0(3)$.

Ta có: $21{\displaystyle \frac{1}{6}};\sqrt{49}>0>-\sqrt{144};-614,1;-111,0(3)$.

Xét

     $\begin{array}{l}21{\displaystyle \frac{1}{6}};\sqrt{49}:\\ 21{\displaystyle \frac{1}{6}}={\displaystyle \frac{127}{6}}=21,1(6)\\ \sqrt{49}=7\\ \Rightarrow 21{\displaystyle \frac{1}{6}}>\sqrt{49}\end{array}$

Xét

     $\begin{array}{l}-\sqrt{144};-614,1;-111,0(3):\\ -\sqrt{144}=-12\\ \Rightarrow -\sqrt{144}>-111,0(3)>-614,1\end{array}$

Vậy các số sắp xếp theo thứ tự giảm dần là: $21{\displaystyle \frac{1}{6}};\sqrt{49};-\sqrt{144};-111,0(3);-614,1$.

Bài 83 trang 65 sách bài tập Toán 7: Tính:

a) $\sqrt{0,04}+\sqrt{0,25}+2,31$;

b) $(-\sqrt{0,09})+(-\sqrt{169})+12,501$;

c) ${\displaystyle \frac{\sqrt{49}}{\sqrt{4}}}+{\displaystyle \frac{\sqrt{225}}{\sqrt{144}}}-3,5$;

d) $(-\sqrt{0,04}).\sqrt{0,01}+12,02$;

e) $\left|{\displaystyle \frac{-11}{3}}\right|+{\left({\displaystyle \frac{-1}{2}}\right)}^2-\left|4{\displaystyle \frac{1}{2}}+(-3,25)\right|$;

g) $\left|\sqrt{169}-\sqrt{900}\right|-\left|{\displaystyle \frac{-5}{4}}\right|:{\left({\displaystyle \frac{1}{3}}-{\displaystyle \frac{1}{2}}\right)}^2$.

Lời giải:

a) $\sqrt{0,04}+\sqrt{0,25}+2,31=0,2+0,5+2,31=0,7+2,31=3,01$;

b) $(-\sqrt{0,09})+(-\sqrt{169})+12,501=-0,3+(-13)+12,501=-0,799$;

c) ${\displaystyle \frac{\sqrt{49}}{\sqrt{4}}}+{\displaystyle \frac{\sqrt{225}}{\sqrt{144}}}-3,5={\displaystyle \frac{7}{2}}+{\displaystyle \frac{15}{12}}-3,5=3,5+1,25-3,5=1,25$;

d) $(-\sqrt{0,04}).\sqrt{0,01}+12,02=-0,2.0,1+12,02=-0,02+12,02=12$;

e)

$\begin{array}{l}\left|{\displaystyle \frac{-11}{3}}\right|+{\left({\displaystyle \frac{-1}{2}}\right)}^2-\left|4{\displaystyle \frac{1}{2}}+(-3,25)\right|={\displaystyle \frac{11}{3}}+{\displaystyle \frac{1}{4}}-\left|{\displaystyle \frac{9}{2}}-3,25\right|\\ ={\displaystyle \frac{11}{3}}+{\displaystyle \frac{1}{4}}-\left|4,5-3,25\right|={\displaystyle \frac{11}{3}}+{\displaystyle \frac{1}{4}}-\left|1,25\right|={\displaystyle \frac{11}{3}}+{\displaystyle \frac{1}{4}}-{\displaystyle \frac{5}{4}}\\ ={\displaystyle \frac{8}{3}}\end{array}$

g)

 $\begin{array}{l}\left|\sqrt{169}-\sqrt{900}\right|-\left|{\displaystyle \frac{-5}{4}}\right|:{\left({\displaystyle \frac{1}{3}}-{\displaystyle \frac{1}{2}}\right)}^2=\left|13-30\right|-{\displaystyle \frac{5}{4}}:{\left({\displaystyle \frac{-1}{6}}\right)}^2\\ =\left|-17\right|-{\displaystyle \frac{5}{4}}:{\displaystyle \frac{1}{36}}=17-{\displaystyle \frac{5}{4}}.36=17-45=-28\end{array}$

Bài 84 trang 66 sách bài tập Toán 7: Tìm x, biết:

a) $x+{\displaystyle \frac{6}{23}}+(-0,7)+{\displaystyle \frac{17}{23}}=0$;

b) $\left|x\right|-{\displaystyle \frac{1}{2}}={\displaystyle \frac{9}{2}}$;

c) $2x+\sqrt{0,81}-\left|{\displaystyle \frac{-5}{4}}\right|:{\left(-{\displaystyle \frac{1}{2}}\right)}^2=-0,1$;

d*) $\left|x\right|+\left|x+1\right|={\displaystyle \frac{-3}{4}}$.

Lời giải:

a)

 $\begin{array}{l}x+{\displaystyle \frac{6}{23}}+(-0,7)+{\displaystyle \frac{17}{23}}=0\\ x+{\displaystyle \frac{6}{23}}-0,7+{\displaystyle \frac{17}{23}}=0\\ x={\displaystyle \frac{-17}{23}}+0,7-{\displaystyle \frac{6}{23}}\\ x={\displaystyle \frac{-23}{23}}+0,7\\ x=-1+0,7\\ x=-0,3\end{array}$

Vậy $x=-0,3$.

b)

 $\begin{array}{l}\left|x\right|-{\displaystyle \frac{1}{2}}={\displaystyle \frac{9}{2}}\Rightarrow \left|x\right|={\displaystyle \frac{9}{2}}+{\displaystyle \frac{1}{2}}={\displaystyle \frac{10}{2}}=5\\ \Rightarrow [\begin{array}{l}x=5\\ x=-5\end{array}\end{array}$

Vậy $x=5;x=-5$.

c)

 $\begin{array}{l}2x+\sqrt{0,81}-\left|{\displaystyle \frac{-5}{4}}\right|:{\left(-{\displaystyle \frac{1}{2}}\right)}^2=-0,1\\ 2x+0,9-{\displaystyle \frac{5}{4}}:{\displaystyle \frac{1}{4}}=-0,1\\ 2x+0,9-5=-0,1\\ 2x=-0,1+5-0,9\\ 2x=4\\ x=4:2\\ x=2\end{array}$

Vậy $x=2$.

d*) $\left|x\right|+\left|x+1\right|={\displaystyle \frac{-3}{4}}$.

Ta thấy: $\{\begin{array}{l}\left|x\right|\ge 0\mathrm{\forall }x\\ \left|x+1\right|\ge 0\mathrm{\forall }x\end{array}$.

Suy ra: $\left|x\right|+\left|x+1\right|\ge 0\mathrm{\forall }x$.

Mà ${\displaystyle \frac{-3}{4}}<0$ nên không tồn tại giá trị nào của x thỏa mãn $\left|x\right|+\left|x+1\right|={\displaystyle \frac{-3}{4}}$ . 

Bài 85 trang 66 sách bài tập Toán 7: Chỉ số đo đồng hồ nước sinh hoạt của nhà bạn Hạnh được thống kê theo bảng sau:

Tổng số tiền nước nhà bạn Hạnh phải trả trong Quý III là 354 200 đồng. Tính số tiền nước nhà bạn Hạnh phải trả trong mỗi tháng Quý III, biết rằng giá mỗi mét khối nước hằng tháng là như nhau.

Lời giải:

Số nước nhà bạn Hạnh dùng trong Quý III là:

$250-204=46({\mathrm{m}}^3)$.

Giá tiền 1 m³ nước là:

$354200:46=7700$ (đồng).

Vậy số tiền nước nhà bạn Hạnh trả trong mỗi tháng Quý III là:

Tháng 7: $7700.(220-204)=123200$ (đồng).

Tháng 8: $7700.(237-220)=130900$ (đồng).

Tháng 9: $7700.(250-237)=100100$ (đồng).

Bài 86 trang 66 sách bài tập Toán 7: Tìm ba số x, y, z biết:

a) $2x=3y;5y=7z$ và $3x-7y+5z=30$;

b) ${\displaystyle \frac{x-1}{2}}={\displaystyle \frac{y-2}{3}}={\displaystyle \frac{z-3}{4}}$ và $x-2y+3z=14$.

Lời giải:

a) $2x=3y;5y=7z$ và $3x-7y+5z=30$;

Ta có:

$\begin{array}{l}2x=3y;5y=7z\to {\displaystyle \frac{x}{3}}={\displaystyle \frac{y}{2}};{\displaystyle \frac{y}{7}}={\displaystyle \frac{z}{5}}\\ \to {\displaystyle \frac{x}{21}}={\displaystyle \frac{y}{14}}={\displaystyle \frac{z}{10}}\end{array}$

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

${\displaystyle \frac{x}{21}}={\displaystyle \frac{y}{14}}={\displaystyle \frac{z}{10}}={\displaystyle \frac{3x-7y+5z}{3.21-7.14+5.10}}={\displaystyle \frac{30}{15}}=2$.

Do đó: $\{\begin{array}{l}x=2.21=42\\ y=2.14=28\\ x=2.10=20\end{array}$.

b) ${\displaystyle \frac{x-1}{2}}={\displaystyle \frac{y-2}{3}}={\displaystyle \frac{z-3}{4}}$ và $x-2y+3z=14$.

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\begin{array}{l}{\displaystyle \frac{x-1}{2}}={\displaystyle \frac{y-2}{3}}={\displaystyle \frac{z-3}{4}}={\displaystyle \frac{x-1-2(y-2)+3(z-3)}{2-2.3+3.4}}={\displaystyle \frac{x-1-2y+4+3z-9}{8}}\\ ={\displaystyle \frac{x-2y+3z-6}{8}}={\displaystyle \frac{14-6}{8}}={\displaystyle \frac{8}{8}}=1\end{array}$

Do đó: $\{\begin{array}{l}x=1.2+1=3\\ y=1.3+2=5\\ z=1.4+3=7\end{array}$. 

Bài 87 trang 66 sách bài tập Toán 7: Một chiếc xe đạp và một chiếc xe máy cùng một lúc đi từ A đến B. Vận tốc của xe máy lớn hơn vận tốc của xe đạp là 18 km/h nên khi xe máy đến B thì xe đạp đến C (C nằm giữa A và B). Quãng đường CB bằng 0,6 lần quãng đường AB. Tính vận tốc của mỗi xe.

Lời giải:

Gọi vận tốc của xe đạp và xe máy lần lượt là x, y (km/h).

Quãng đường CB bằng 0,6 lần quãng đường AB nên quãng đường AC bằng 0,4 lần quãng đường AB.

Do cùng một quãng đường thì vận tốc và quãng đường là hai đại lượng tỉ lệ thuận nên

${\displaystyle \frac{x}{y}}={\displaystyle \frac{AC}{AB}}=0,4={\displaystyle \frac{2}{5}}\to {\displaystyle \frac{x}{2}}={\displaystyle \frac{y}{5}}$.

Mà vận tốc của xe máy lớn hơn vận tốc của xe đạp là 18 km/h nên $y-x=18$.

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

${\displaystyle \frac{x}{2}}={\displaystyle \frac{y}{5}}={\displaystyle \frac{y-x}{5-2}}={\displaystyle \frac{18}{3}}=6$.

Do đó: $\{\begin{array}{l}x=6.2=12\\ y=6.5=30\end{array}$.

Vậy vận tốc của xe đạp là 12 km/h, vận tốc của xe máy là 30 km/h.

Bài 88 trang 66 sách bài tập Toán 7: Chị Hà đã chuẩn bị sẵn một số tiền để mua 15 kg cá hồi tại một cửa hàng hải sản. Nhưng hôm đó, nhân dịp năm mới nên cửa hàng đã giảm giá 20% mỗi ki-lô-gam cá hồi. Với số tiền đã chuẩn bị, chị Hà mua thêm được nhiều nhất bao nhiêu ki-lô-gam cá hồi?