Với giải Bài 7 trang 86 Toán lớp 10 Tập 2 Cánh diều chi tiết trong Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Giải bài tập Toán 10 Bài 7 trang 86 Toán lớp 10 Tập 2

Bài 7 trang 86 Toán lớp 10 Tập 2: Có hai con tàu A và B cùng xuất phát từ hai bến, chuyển động đều theo đường thẳng ngoài biển. Trên màn hình ra đa của trạm điều khiển (được coi như mặt phẳng tọa độ Oxy với đơn vị trên các trục tính theo ki-lô-mét), sau khi xuất phát t (giờ) (t$\ge$0), vị trí của tàu A có tọa độ được xác định bởi công thức 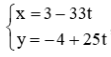, vị trí của tàu B có tọa độ là (4-30t ; 3-40t).

a) Tính côsin góc giữa hai đường đi của hai tàu A và B.

b) Sau bao lâu kể từ thời điểm xuất phát hai tàu gần nhau nhất?

c) Nếu tàu A đứng yên ở vị trí ban đầu, tàu B chạy thì khoảng cách ngắn nhất giữa hai tàu bằng bao nhiêu?

Lời giải:

a) Giả sử đường đi của tàu A là d₁, khi đó phương trình d₁:

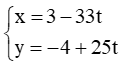
Giả sử đường đi của tàu B là d₂, vị trí của tàu B có tọa độ là (4 – 30t; 3 – 40t) nên phương trình d₂:

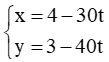
Đường thẳng d₁ có vectơ chỉ phương là $\overrightarrow{u_1}=\left(-33;25\right)$.

Đường thẳng d₂ có vectơ chỉ phương là $\overrightarrow{u_2}=\left(-30;-40\right)$.

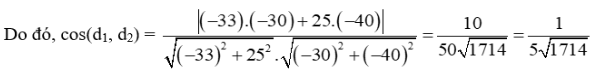
Vậy côsin góc giữa hai đường đi của hai tàu A và B là $\frac{1}{5\sqrt{1714}}$.

b) Đường thẳng d₁ đi qua điểm A(3; – 4) và có một vectơ pháp tuyến là $\overrightarrow{n_1}=\left(25;33\right)$.

Do đó phương trình tổng quát của d₁ là 25(x – 3) + 33(y + 4) = 0 hay 25x + 33y + 57 = 0.

Đường thẳng d₂ đi qua điểm B(4; 3) và có một vectơ pháp tuyến là $\overrightarrow{n_2}=\left(4;-3\right)$.

Do đó phương trình tổng quát của d₂ là 4(x – 4) – 3(y – 3) = 0 hay 4x – 3y – 7 = 0.

Tọa độ giao điểm của hai đường thẳng d₁ và d₂ là nghiệm của hệ phương trình

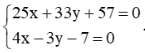
Do đó hai đường thẳng d1 và d2 cắt nhau tại điểm có tọa độ $\left(\frac{20}{69};-\frac{403}{207}\right)$.

Khi đó hai tàu A và tàu B gần nhau nhất khi hai tàu ở vị trí tọa độ $\left(\frac{20}{69};-\frac{403}{207}\right)$.

Thay tọa độ $\left(\frac{20}{69};-\frac{403}{207}\right)$ vào phương trình tham số d₁ ta được:

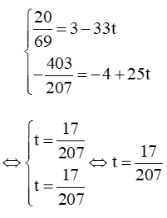
Vậy sau $\frac{17}{207}$ giờ kể từ thời điểm xuất phát thì hai tàu gần nhau nhất.

c) Vì tàu A đứng yên ở vị trí ban đầu nên thời gian tàu A chạy là t = 0, do đó tàu A đứng ở vị trí A(3; – 4).

Khi đó khoảng cách ngắn nhất giữa hai tàu chính là khoảng cách từ điểm A đến đường đi của tàu B chính là đường thẳng d2: 4x – 3y – 7 = 0.

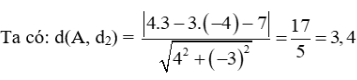
Vậy nếu tàu A đứng yên ở vị trí ban đầu, tàu B chạy thì khoảng cách ngắn nhất giữa hai tàu bằng 3,4 km.

Xem thêm các bài giải Toán 10 Kết nối tri thức hay, chi tiết khác:

Câu hỏi khởi động trang 81 Toán lớp 10 Tập 2: Trong thực tiễn, có những tình huống đòi hỏi chúng ta phải xác định

Hoạt động 1 trang 81 Toán lớp 10 Tập 2: Nêu vị trí tương đối của hai đường thẳng trong mặt phẳng

Hoạt động 2 trang 81 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ, cho hai đường thẳng ∆₁, ∆₂ lần lượt

Luyện tập 1 trang 82 Toán lớp 10 Tập 2: Xét vị trí tương đối của hai đường thẳng

Luyện tập 2 trang 82 Toán lớp 10 Tập 2: Xét vị trí tương đối của đường thẳng d: x + 2y – 2 = 0 với mỗi đường thẳng sau

Hoạt động 3 trang 83 Toán lớp 10 Tập 2: Trong mặt phẳng, cho hai đường thẳng ∆₁ và ∆₂ cắt nhau tại A tạo thành

Hoạt động 4 trang 83 Toán lớp 10 Tập 2: Cho hai đường thẳng ∆₁, ∆₂ cắt nhau tại I và có vectơ chỉ phương lần

Hoạt động 5 trang 84 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ, cho hai đường thẳng ∆₁ và ∆₂ có vectơ chỉ

Luyện tập 3 trang 84 Toán lớp 10 Tập 2: Tính số đo góc giữa hai đường thẳng ∆₁ và ∆₂ trong mỗi trường hợp sau:

Hoạt động 6 trang 85 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ, cho đường thẳng ∆: 2x + y – 4 = 0 và điểm M(– 1; 1)

Luyện tập 4 trang 85 Toán lớp 10 Tập 2: a) Tính khoảng cách từ điểm O(0; 0) đến đường thẳng

Bài 1 trang 86 Toán lớp 10 Tập 2: Xét vị trí tương đối của mỗi cặp đường thẳng sau:

Bài 2 trang 86 Toán lớp 10 Tập 2: Tính số đo góc giữa hai đường thẳng d₁: 2x – y + 5 = 0 và d₂: x – 3y + 3 = 0.

Bài 3 trang 86 Toán lớp 10 Tập 2: Tính khoảng cách từ một điểm đến một đường thẳng trong mỗi trường hợp sau:

Bài 4 trang 86 Toán lớp 10 Tập 2: Với giá trị nào của tham số m thì hai đường thẳng sau đây vuông góc?

Bài 5 trang 86 Toán lớp 10 Tập 2: Cho ba điểm A(2; – 1), B(1; 2) và C(4; – 2). Tính số đo góc BAC

Bài 6 trang 86 Toán lớp 10 Tập 2: Cho ba điểm A(2; 4), B(– 1; 2) và C(3; – 1). Viết phương trình đường thẳng