Với giải Bài 6 trang 92 Toán lớp 10 Tập 2 Cánh diều chi tiết trong Bài 5: Phương trình đường tròn giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Giải bài tập Toán 10 Bài 6 trang 92 Toán lớp 10 Tập 2

Bài 6 trang 92 Toán lớp 10 Tập 2: Hình 46 mô phỏng một trạm thu phát sóng điện thoại di động đặt ở vị trí I có toạ độ (– 2; 1) trong mặt phẳng toạ độ (đơn vị trên hai trục là ki-lô-mét).

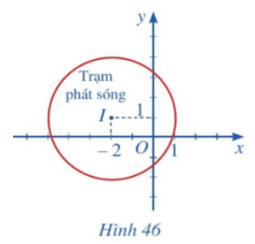
a) Lập phương trình đường tròn mô tả ranh giới bên ngoài của vùng phủ sóng, biết rằng trạm thu phát sóng đó được thiết kế với bán kính phủ sóng 3 km.

b) Nếu người dùng điện thoại ở vị trí có toạ độ (– 1; 3) thì có thể sử dụng dịch vụ của trạm này không? Giải thích.

c) Tính theo đường chim bay, xác định khoảng cách ngắn nhất để một người ở vị trí có toạ độ (– 3; 4) di chuyển được tới vùng phủ sóng theo đơn vị ki-lô-mét (làm tròn kết quả đến hàng phần mười).

Lời giải:

a) Đường tròn mô tả ranh giới bên ngoài của vùng phủ sóng có tâm I(– 2; 1) và bán kính R = 3.

Do đó, phương trình đường tròn cần lập là (x + 2)² + (y – 1)² = 9.

b) Khoảng cách từ tâm I của đường tròn ranh giới tới vị trí có tọa độ (– 1; 3) là

d = $\sqrt{{\left(\left(-1\right)-\left(-2\right)\right)}^2+{\left(3-1\right)}^2}=\sqrt{5}$.

Vì $\sqrt{5}<3$ nên d < R.

Do đó, vị trí có tọa độ (– 1; 3) nằm bên trong đường tròn mô tả ranh giới bên ngoài của vùng phủ sóng.

Vậy người dùng điện thoại ở vị trí có tọa độ (– 1; 3) có thể sử dụng dịch vụ của trạm này.

c) Gọi vị trí người đó đang đứng là B(– 3; 4).

Ta có: $\overrightarrow{BI}=\left(-2-\left(-3\right);1-4\right)=\left(1;-3\right)$, $BI=\sqrt{1^2+{\left(-3\right)}^2}=\sqrt{10}$.

BI > R nên B nằm ngoài đường tròn ranh giới, giả sử đường thẳng BI cắt đường tròn tại điểm A, khi đó AB là khoảng cách ngắn nhất từ B đến vùng phủ sóng.

Ta cần tìm tọa độ điểm A.

Đường thẳng BI có một vectơ chỉ phương là vectơ $\overrightarrow{BI}$ nên nó có một vectơ pháp tuyến là $\overrightarrow{n}=\left(3;1\right)$. Do đó, phương trình đường thẳng BI là 3(x + 3) + 1(y – 4) = 0 hay 3x + y + 5 = 0.

+ Với $A\left(\frac{-20+3\sqrt{10}}{10};\frac{10-9\sqrt{10}}{10}\right)$

Ta có: $AB=\sqrt{{\left(-3-\frac{-20+3\sqrt{10}}{10}\right)}^2+{\left(4-\frac{10-9\sqrt{10}}{10}\right)}^2}\approx 6,2$

+ Với $A\left(\frac{-20-3\sqrt{10}}{10};\frac{10+9\sqrt{10}}{10}\right)$

Ta có: $AB=\sqrt{{\left(-3-\frac{-20-3\sqrt{10}}{10}\right)}^2+{\left(4-\frac{10+9\sqrt{10}}{10}\right)}^2}\approx 0,2$

Do 0,2 < 6,2 nên ta chọn kết quả 0,2.

Vậy tính theo đường chim bay, khoảng cách ngắn nhất để một người ở vị trí có toạ độ (– 3; 4) di chuyển được tới vùng phủ sóng là 0,2 km.

Xem thêm các bài giải Toán 10 Kết nối tri thức hay, chi tiết khác:

Câu hỏi khởi động trang 87 Toán lớp 10 Tập 2: Ở một số công viên, người ta dựng vòng quay có bán kính rất lớn

Hoạt động 1 trang 87 Toán lớp 10 Tập 2: a) Tính khoảng cách từ gốc tọa độ O(0; 0) đến điểm M(3; 4) trong mặt

Hoạt động 2 trang 87 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, nêu mối liên hệ giữa x và y để:

Luyện tập 1 trang 88 Toán lớp 10 Tập 2: Viết phương trình đường tròn tâm I(6; – 4) đi qua điểm A(8; – 7)

Hoạt động 3 trang 88 Toán lớp 10 Tập 2: Viết phương trình đường tròn (C): (x – a)² + (y – b)² = R² về dạng x² + y² – 2ax – 2by + c = 0.

Luyện tập 2 trang 89 Toán lớp 10 Tập 2: Tìm k sao cho phương trình: x2 + y2 + 2kx + 4y + 6k – 1 = 0 là phương

Luyện tập 3 trang 89 Toán lớp 10 Tập 2: Lập phương trình đường tròn đi qua ba điểm A(1; 2), B(5; 2), C(1; – 3).

Hoạt động 4 trang 90 Toán lớp 10 Tập 2: Cho điểm M₀(x₀; y₀) nằm trên đường tròn (C) tâm I(a; b) bán kính R.

Luyện tập 4 trang 90 Toán lớp 10 Tập 2: Lập phương trình tiếp tuyến tại điểm M₀(– 1; – 4) thuộc đường tròn

Bài 1 trang 91 Toán lớp 10 Tập 2: Phương trình nào sau đây là phương trình đường tròn?

Bài 2 trang 91 Toán lớp 10 Tập 2: Tìm tâm và bán kính của đường tròn trong mỗi trường hợp sau:

Bài 3 trang 91 Toán lớp 10 Tập 2: Lập phương trình đường tròn trong mỗi trường hợp sau:

Bài 4 trang 92 Toán lớp 10 Tập 2: Lập phương trình tiếp tuyến tại điểm có hoành độ bằng 3 thuộc đường tròn

Bài 5 trang 92 Toán lớp 10 Tập 2: Tìm m sao cho đường thẳng 3x + 4y + m = 0 tiếp xúc với đường tròn

Bài 7 trang 92 Toán lớp 10 Tập 2: Ném đĩa là một môn thể thao thi đấu trong Thế vận hội Olympic mùa hè. Khi