Toptailieu.vn giới thiệu Giải bài tập Toán lớp 6 Bài 9: Ước và bộisách Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán lớp 6 Tập 1. Mời các bạn đón xem:

Toán 6 (Chân trời sáng tạo) Bài 9: Ước và bội

Câu hỏi giữa bài

Toán 6 trang 28 Hoạt động khám phá 1: Lớp 6A có 36 học sinh. Trong một tiết mục đồng diễn thể dục nhịp điệu, lớp xếp thành đội hình gồm những hàng đều nhau. Hãy hoàn thành bảng sau vào vở để tìm các cách mà lớp có thể xếp đội hình.

b) Viết số 36 thành tích của hai số bằng các cách khác nhau.

Lời giải 

b)

$36=1.36=2.18=3.12=4.9=6.6$

Toán 6 trang 28 Thực hành 1: Chọn từ thích hợp trong các từ “ước”,  “bội” thay thế dấu ? ở mỗi câu sau để có khẳng định đúng.

b) Hãy chỉ ra các ước của 6. Số 6 là bội của những số nào?

Lời giải

i. 48 là bội của 6

ii. 12 là ước của 48

iii. 48 là bội của 48 hoặc 48 là ước của 48

iv. 0 là bội của 48

b) Các ước của 6 là: 1; 2; 3; 6

   Số 6 là bội của 1; 2; 3; 6

Toán 6 trang 29 Hoạt động khám phá 2: Số 18 có thể chia hết cho những số nào?

Lời giải 

18 có thể chia hết cho: 1; 2; 3; 6; 9; 18

Toán 6 trang 29 Thực hành 2: Hãy tìm các tập hợp sau:

a) Ư(17);                     b) Ư(20).

Lời giải 

a)

Ư(17) = {1; 17}

b)

Ư(20) = {1; 2; 4; 5; 10; 20}

Toán 6 trang 29 Hoạt động khám phá 3: Chuẩn bị một số mảnh giấy nhỏ có chiều dài là 3 cm. Ghép các mảnh giấy nhỏ đó thành các bằng giấy như hình minh hoạ dưới đây:

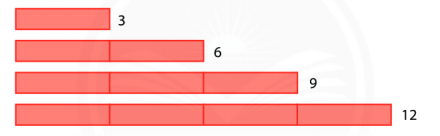
Độ dài bằng giấy đầu tiên là: 3.1 = 3 (cm);

Độ dài bằng giấy thứ hai là: 3.2=6 (cm);

Tiếp tục cách đó, ta có thể tính độ dài các bằng giấy thứ ba, thứ tư lần lượt là: 3.3=9 (cm); 3.4 = 12 (cm);

- Hãy tính độ dài của hai bằng giấy tiếp theo.

- Nêu nhận xét về mối liên hệ giữa số đo độ dài (cm) của các bằng giấy nói trên với 3.

b) Làm thế nào để tìm được các bội của 3 một cách nhanh chóng?

Lời giải 

a) Độ dài hai băng giấy tiếp theo là:

3.5 = 15;         3.6 = 18

Độ dài của các cuộn băng giấy là bội của 3

b) Ta nhân 3 lần lượt với các số 0; 1; 2; 3; 4; 5;…

Toán 6 trang 30 Thực hành 3: Hãy tìm các tập hợp sau:

a) B(4);            b) B(7).

Lời giải 

B(4) = {0; 4; 8; 12; 16;…}

B(7) = {0; 7; 14; 21;…}

Bài tập trang 30

Toán 6 trang 30 Bài 1: Chọn kí hiệu $\in$ hoặc $\notin$ thay cho dấu ?  trong mỗi câu sau để được các kết luận đúng.

Lời giải

a) 6$\in$Ư(48);                b) 12 $\notin$Ư(30);                             

c) 7$\in$ Ư(42);               d) 18$\notin$B(4);                               

e) 28$\in$B(7);                 g)36$\in$B(12).

Toán 6 trang 30 Bài 2: a) Tìm tập hợp các ước của 30.

b) Tìm tập hợp các bội của 6 nhỏ hơn 50.

c) Tìm tập hợp C các số tự nhiên x sao cho x vừa là bội của 18, vừa là ước của 72.

Lời giải 

a) Ư(30) = {1; 2; 3; 5; 6; 10; 15; 30}

b) B(6) = {0; 6; 12; 18; 24; 30; 36; 42; 48}

c) B(18) = {0; 18; 36; 54; 72; …}

  Ư(72) = {1; 2; 3; 4; 6; 8; 9; 12; 18; 24; 36; 72}

=> x$\in${18; 36; 72}

Toán 6 trang 30 Bài 3: Viết mỗi tập hợp sau bằng cách liệt kê các phần tử.

a) A = {x $\in$ Ư(40) | x > 6}; b) B = {x $\in$ B(12) | 24 $\le$x $\le$ 60}.

Lời giải 

a) A = {8; 10; 20; 40}

b) B = {24; 36; 48; 60}

Toán 6 trang 30 Bài 4: Trò chơi “Đua viết số cuối cùng”

Bình và Minh chơi trò chơi “đua viết số cuối cùng”. Hai bạn thi viết các số theo luật như sau:

Người chơi thứ nhất sẽ viết một số tự nhiên không lớn hơn 3. Sau đó đến lượt người thứ hai viết rồi quay lại người thứ nhất và cứ thế tiếp tục, ... sao cho kể từ sau số viết đầu tiên, mỗi bạn viết một số lớn hơn số bạn mình vừa viết nhưng không lớn hơn quá 3 đơn vị. Ai viết được số 20 trước thì người đó thắng. Sau một số lần chơi, Minh thấy Bình luôn thắng. Minh thắc mắc: “Sao lúc nào cậu cũng thắng tớ thế?”. Bình cười: “Không phải lúc nào tớ cũng thắng được cậu đâu”.

a) Bình đã chơi như thế nào để thắng được Minh? Minh có thể thắng được Bình khi nào?

b) Hãy chơi cùng bạn trò chơi trên. Em hãy đề xuất một luật chơi mới cho trò chơi trên rồi chơi cùng các bạn.

Lời giải 

a)*Bình đã chơi như sau:

+) TH1: Minh viết trước

=> Bình luôn viết các số là bội của 4

+) TH2: Minh viết sau

=> Bình viết số 0 đầu tiên và các số sau là bội của 4

*Minh có thể thắng Bình khi Minh biết quy luật và Minh đi trước

b) Đề xuất luật chơi mới:

Người chơi thứ nhất sẽ viết một số tự nhiên không lớn hơn 3. Sau đó đến lượt người thứ hai viết rồi quay lại người thứ nhất và cứ thế tiếp tục, ... sao cho kể từ sau số viết đầu tiên, mỗi bạn viết một số lớn hơn số bạn mình vừa viết nhưng không lớn hơn quá 3 đơn vị. Ai viết được số 25 trước thì người đó thắng.

Toán 6 trang 30 Em có biết: Theo dương lịch, một năm thường có 365 ngày, riêng năm nhuận có thêm 1 ngày và ngày đó được cố định là ngày 29 tháng Hai. Thông thường, năm nhuận có số năm là bội của 4. Các năm 2044, 2086 có phải năm nhuận không?

Lời giải 

2044 là bội của 4 nên năm 2044 là năm nhuận

2086 không là bội của 4 nên năm 2086 không phải năm nhuận