Toptailieu.vn giới thiệu Vở bài tập Toán 8 trang 68, 69, 70, 71, 72, 73, 74 Bài 2: Định lí đảo và hệ quả của định lí Ta – lét chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong Vở bài tập Toán 8. Mời các bạn đón đọc.

Vở bài tập Toán 8 trang 68, 69, 70, 71, 72, 73, 74 Bài 2: Định lí đảo và hệ quả của định lí Ta – lét

Câu hỏi Vở bài tập Toán 8 trang 68 - 74:

Câu 4. Ghi phần kết luận vào chỗ trống.

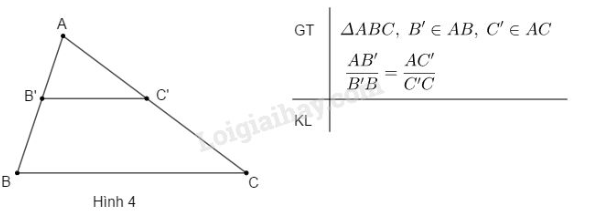
Phương pháp giải:

Áp dụng:

- Định lí đảo: Nếu một đường thẳng cắt hai cạnh một tam giác và định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác. 

Lời giải:

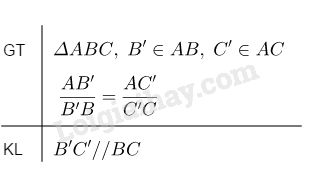
Câu 5. Ghi phần kết luận vào chỗ trống

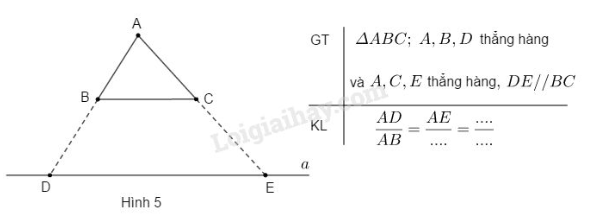
Phương pháp giải:

Áp dụng:

- Hệ quả của định lí Talet: Nếu một đường thẳng cắt hai cạnh còn lại của một của một tam giác và song song với các cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh còn lại của tam giác đã cho

Lời giải:

Câu 6. Ghi phần kết luận vào chỗ trống.

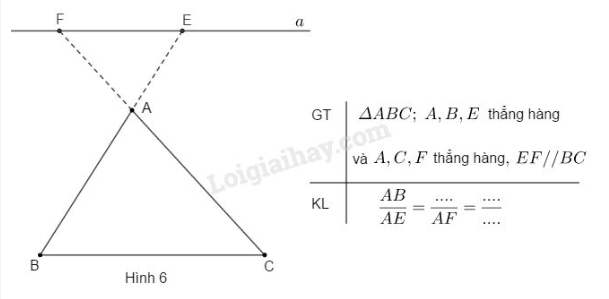
Phương pháp giải:

Áp dụng:

- Hệ quả của định lí Talet: Nếu một đường thẳng cắt hai cạnh còn lại của một của một tam giác và song song với các cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh còn lại của tam giác đã cho.

- Chú ý: Trường hợp đường thẳng a song song với một cạnh của tam giác và cắt phần còn lại kéo dài của hai cạnh còn lại hệ quả vẫn đúng.

Lời giải:

Vở bài tập Toán 8 trang 68 - 74 Bài 4: Tìm các cặp đường thẳng song song trong hình 7 và giải thích vì sao chúng song song.

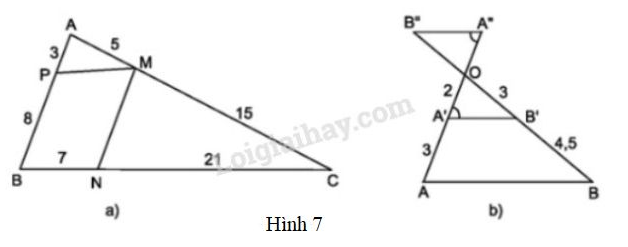
Phương pháp giải:

- Áp dụng định lý TaLet đảo: Nếu một đường thẳng cắt hai cạnh một tam giác và định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.

- Dấu hiệu nhận biết hai đường thẳng song song.

Lời giải

a) Xét $\mathrm{\Delta }ABC$ và đường thẳng $PM$ (h.7a) ta thấy:

${\displaystyle \frac{AP}{PB}}={\displaystyle \frac{3}{8}}$; ${\displaystyle \frac{AM}{MC}}={\displaystyle \frac{5}{15}}={\displaystyle \frac{1}{3}}$; ${\displaystyle \frac{3}{8}}\ne {\displaystyle \frac{1}{3}}$

Suy ra $PM$ không song song với $BC$.

Xét $\mathrm{\Delta }ABC$ và đường thẳng $MN$ (h.7a) ta thấy:

${\displaystyle \frac{AM}{MC}}={\displaystyle \frac{5}{15}};{\displaystyle \frac{BN}{NC}}={\displaystyle \frac{7}{21}};{\displaystyle \frac{5}{15}}={\displaystyle \frac{7}{21}}$

Vậy ${\displaystyle \frac{AM}{MC}}={\displaystyle \frac{BN}{NC}}$

Áp dụng định lí Ta - lét đảo, suy ra $MN//AB$.

b) So sánh các góc so le trong, ta thấy $\widehat{B^{″}{A}^{″}{A}^{\prime }}=\widehat{A^{″}{A}^{\prime }{B}^{\prime }}$ (h.7b)

Vậy $A^{\prime }{B}^{\prime }//A^{″}{B}^{″}$.

Xét $\mathrm{\Delta }AOB$ và đường thẳng $A^{\prime }{B}^{\prime }$, ta thấy:

${\displaystyle \frac{O{A}^{\prime }}{A^{\prime }A}}={\displaystyle \frac{2}{3}}$; ${\displaystyle \frac{O{B}^{\prime }}{B^{\prime }B}}={\displaystyle \frac{3}{4,5}};$ ${\displaystyle \frac{2}{3}}={\displaystyle \frac{3}{4,5}}.$ 

Vậy: ${\displaystyle \frac{O{A}^{\prime }}{A^{\prime }A}}={\displaystyle \frac{O{B}^{\prime }}{B^{\prime }B}}$ 

Áp dụng định lí TaLet đảo, suy ra $A^{\prime }{B}^{\prime }//AB$.

Từ các kết quả trên, ta có: $A^{″}{B}^{″}//A^{\prime }{B}^{\prime }//AB$.

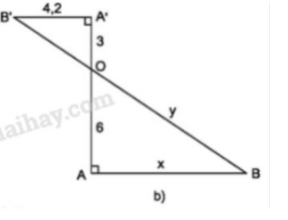
Vở bài tập Toán 8 trang 68 - 74 Bài 5: Tính các độ dài  trong hình 8.

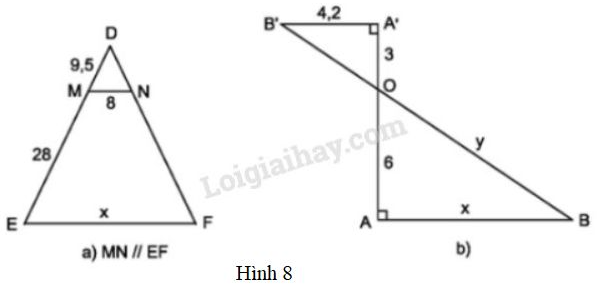
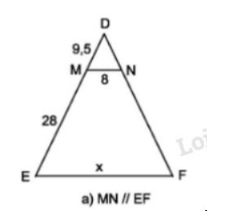
Phương pháp giải:

a, - Áp dụng: hệ quả của định lý TaLet, định lý Pitago.

b, - Áp dụng: hệ quả của định lý TaLet, định lý Pitago.

Lời giải :

a,

$MN//EF$ (h.8a). Theo hệ quả định lí Ta-lét ta có:

$\frac{DM}{DE}=\frac{MN}{EF}$ hay ${\displaystyle \frac{9,5}{(9,5+28)}}={\displaystyle \frac{8}{x}}$

Vậy $x={\displaystyle \frac{8.(9,5+28)}{9,5}}$

Tính trên máy tính bỏ túi, ta được $x\approx 31,57894737$.

Lấy chính xác đến hai chữ số thập phân, ta có: $x\approx 31,58$

b,

$A^{\prime }{B}^{\prime }\perp A{A}^{\prime };AB\perp A{A}^{\prime }$ (h.8b)

Suy ra $A^{\prime }{B}^{\prime }//AB$.

Theo hệ quả của định lí Ta - lét, ta có:

${\displaystyle \frac{O{A}^{\prime }}{OA}}={\displaystyle \frac{A^{\prime }{B}^{\prime }}{AB}}$ hay ${\displaystyle \frac{3}{6}}={\displaystyle \frac{4,2}{x}}$

$x={\displaystyle \frac{4,2.6}{3}}=8,4$

Xét tam giác vuông $OAB$:$O{B}^2=O{A}^2+A{B}^2$

hay $y^2=6^2+8,4^2=106,56$

Suy ra $y=\sqrt{106,56}$

Tính trên máy tính bỏ túi được: $y\approx 10,32279032$.

Lấy chính xác đến hai chữ số thập phân, ta được: $y\approx 10,32$.

Từ $D$ và $B$ hạ $DK\mathrm{\perp }AC;BH\mathrm{\perp }AC$

Ta thấy $DK//BH$ (vì cùng vuông góc với $AC$)

Xét $\mathrm{\Delta }ABH$. Theo hệ quả của định lí Ta - lét, ta có:

${\displaystyle \frac{AD}{AB}}={\displaystyle \frac{DK}{BH}}$ hay ${\displaystyle \frac{13,5}{(13,5+4,5)}}={\displaystyle \frac{DK}{BH}}$

Tính trên máy tính bỏ túi, ta được ${\displaystyle \frac{DK}{BH}}={\displaystyle \frac{3}{4}}$.

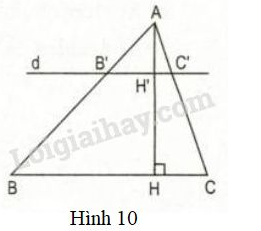
Vở bài tập Toán 8 trang 68 - 74 Bài 7: $∆ABC$ có đường cao $AH$. Đường thẳng $d$ song song với $BC$, cắt các cạnh $AB,AC$ và đường cao $AH$ theo thứ tự tại các điểm $B^{\prime },C^{\prime }$ và $H^{\prime }$(h.16)

a) Chứng minh rằng:

${\displaystyle \frac{A{H}^{\prime }}{AH}}={\displaystyle \frac{B^{\prime }{C}^{\prime }}{BC}}$.

b) Áp dụng: Cho biết $A{H}^{\prime }={\displaystyle \frac{1}{3}}AH$ và diện tích $∆ABC$ là $67,5$ cm²

Tính diện tích $∆A{B}^{\prime }{C}^{\prime }$.

Lời giải:

a) $d//BC$. Theo hệ quả của định lí Ta - lét, ta có:

${\displaystyle \frac{B^{\prime }{C}^{\prime }}{BC}}={\displaystyle \frac{A{B}^{\prime }}{AB}}={\displaystyle \frac{A{C}^{\prime }}{AC}}$   (1)

Xét $∆ABH$. Theo định lí Ta - lét, ta có:

${\displaystyle \frac{A{H}^{\prime }}{AH}}={\displaystyle \frac{A{B}^{\prime }}{AB}}$  (2)

Từ các hệ thức (1) và (2), suy ra ${\displaystyle \frac{B^{\prime }{C}^{\prime }}{BC}}={\displaystyle \frac{A{H}^{\prime }}{AH}}$    (3)

b)

${\displaystyle S_{A{B}^{\prime }{C}^{\prime }}=\frac{1}{2}A{H}^{\prime }.B^{\prime }{C}^{\prime }}$

$S_{ABC}={\displaystyle \frac{1}{2}}AH.BC$

${\displaystyle \frac{S_{A{B}^{\prime }{C}^{\prime }}}{S_{ABC}}}={\displaystyle \frac{{\displaystyle \frac{1}{2}}A{H}^{\prime }.B^{\prime }{C}^{\prime }}{{\displaystyle \frac{1}{2}}AH.BC}}$$={\displaystyle \frac{B^{\prime }{C}^{\prime }}{BC}}.{\displaystyle \frac{A{H}^{\prime }}{AH}}$

Theo giả thiết ở câu b)

$A{H}^{\prime }={\displaystyle \frac{1}{3}}AH\Rightarrow {\displaystyle \frac{A{H}^{\prime }}{AH}}={\displaystyle \frac{1}{3}}$

Từ tỉ lệ thức (3), ta cũng có: ${\displaystyle \frac{B^{\prime }{C}^{\prime }}{BC}}={\displaystyle \frac{A{H}^{\prime }}{AH}}={\displaystyle \frac{1}{3}}$

Suy ra: ${\displaystyle \frac{S_{A{B}^{\prime }{C}^{\prime }}}{S_{ABC}}}={\displaystyle \frac{1}{3}}.{\displaystyle \frac{1}{3}}={\displaystyle \frac{1}{9}}$ $\Rightarrow S_{A{B}^{\prime }{C}^{\prime }}={\displaystyle \frac{1}{9}}{S}_{ABC}$.

Vậy $S_{A{B}^{\prime }{C}^{\prime }}={\displaystyle \frac{1}{9}}.67,5\left(c{m}^2\right)=7,5\left(c{m}^2\right)$

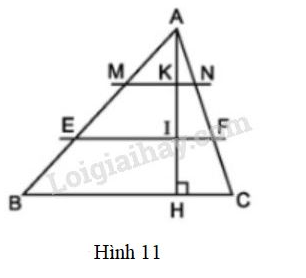
Vở bài tập Toán 8 trang 68 - 74 Bài 8: $∆ABC$ có $BC=15cm$. Trên đường cao $AH$ lấy các điểm $I,K$ sao cho $AK=KI=IH$. Qua $I$ và $K$ vẽ các đường $EF//BC,MN//BC$ (h.11)

a) Tính độ dài đoạn thẳng $MN$ và $EF$.

b) Tính diện tích tứ giác $MNFE$, biết diện tích của $∆ABC$ là $270$ cm²

 a) Xét $∆AEI$ có $MK//EI$ do đó

${\displaystyle \frac{AM}{ME}}={\displaystyle \frac{AK}{KI}}=1\Rightarrow AM=ME$  (1)

Xét $∆ABH$ có $EI//BC$ do đó 

${\displaystyle \frac{AE}{AB}}={\displaystyle \frac{AI}{AH}}={\displaystyle \frac{2}{3}}\Rightarrow AE={\displaystyle \frac{2}{3}}AB$  (2)

Từ (1) và (2) suy ra $AM=ME=EB$.

Theo hệ quả của định lí Ta - lét, ta có:

${\displaystyle \frac{MN}{BC}}={\displaystyle \frac{AM}{AB}}={\displaystyle \frac{1}{3}}$ $\Rightarrow MN={\displaystyle \frac{1}{3}}BC={\displaystyle \frac{1}{3}}.15\left(cm\right)$$=5\left(cm\right).$

${\displaystyle \frac{EF}{BC}}={\displaystyle \frac{AE}{AB}}={\displaystyle \frac{2}{3}}$ $\Rightarrow EF={\displaystyle \frac{2}{3}}BC={\displaystyle \frac{2}{3}}.15\left(cm\right)$$=10\left(cm\right).$

b) Áp dụng kết quả bài 7 ở trên ta có:

${\displaystyle \frac{S_{AMN}}{S_{ABC}}}={\displaystyle \frac{MN.AK}{BC.AH}}$$={\displaystyle \frac{MN}{BC}}.{\displaystyle \frac{AK}{AH}}={\displaystyle \frac{1}{3}}.{\displaystyle \frac{1}{3}}={\displaystyle \frac{1}{9}}$

Suy ra $S_{AMN}={\displaystyle \frac{1}{9}}{S}_{ABC}$

Tương tự, suy ra: $S_{AEF}={\displaystyle \frac{4}{9}}{S}_{ABC}$.

Do đó: $S_{MNEF}=S_{AEF}-S_{AMN}$$={\displaystyle \frac{4}{9}}{S}_{ABC}-{\displaystyle \frac{1}{9}}{S}_{ABC}$$={\displaystyle \frac{1}{3}}{S}_{ABC}$

Với $S_{ABC}=270c{m}^2$, ta có $S_{MNEF}={\displaystyle \frac{1}{3}}.270=90\left(c{m}^2\right).$

Vở bài tập Toán 8 trang 68 - 74 Bài 9: Có thể đo được chiều rộng của một khúc sông mà không cần phải sang bờ bên kia hay không?

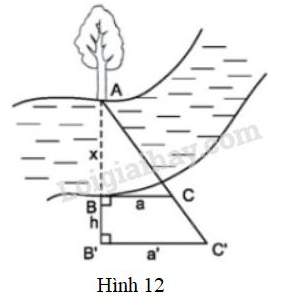
Người ta tiến hành đo đạc các yếu tố hình học cần thiết để tình chiều rộng của khúc sông mà không cần phải sang bờ bên kia (h12). Nhìn hình vẽ, Hãy mô tả những công việc cần làm và tính khoảng cách $AB=x$ theo $BC=a,B^{\prime }{C}^{\prime }=a^{\prime },B{B}^{\prime }=h$.

Phương pháp giải: Áp dụng: Hệ quả của định lý TaLet.
Lời giải:

Mô tả cách làm:

* Chọn một điểm A cố định bên mép bờ sông bên kia (chẳng hạn như là một thân cây), đặt hai điểm B và B' thẳng hàng với A, điểm B sát mép bờ còn lại và $AB$ chính là khoảng cách cần đo.

* Trên hai đường thẳng vuông góc với $A{B}^{\prime }$ tại $B$ và $B^{\prime }$ lấy $C$ và $C^{\prime }$ sao cho $A,C,C^{\prime }$ thẳng hàng.

* Đo độ dài các đoạn $B{B}^{\prime }=h,BC=a,B^{\prime }{C}^{\prime }=a^{\prime }$. Từ đó ta sẽ tính được đoạn $AB=x.$

Giải thích: 

Ta có: $BC\perp A{B}^{\prime }$ và $B^{\prime }{C}^{\prime }\perp A{B}^{\prime }\Rightarrow BC//B^{\prime }{C}^{\prime }$

Xét $\Delta A{B}^{\prime }{C}^{\prime }$ có $BC//B^{\prime }{C}^{\prime }(B\in A{B}^{\prime },C\in A{C}^{\prime })$ 

$\Rightarrow {\displaystyle \frac{AB}{A{B}^{\prime }}}={\displaystyle \frac{BC}{B{C}^{\prime }}}$ (hệ quả định lý Talet) mà $A{B}^{\prime }=x+h$ nên 

${\displaystyle \frac{x}{x+h}}={\displaystyle \frac{a}{a^{\prime }}}$ 

$\iff a^{\prime }x=ax+ah$

$\iff a^{\prime }x-ax=ah$

$\iff x(a^{\prime }-a)=ah$

$\Rightarrow x={\displaystyle \frac{ah}{a^{\prime }-a}}$

Vậy khoảng cách $AB$ bằng ${\displaystyle \frac{ah}{a^{\prime }-a}}$

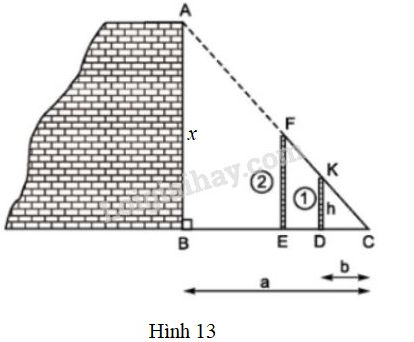
Vở bài tập Toán 8 trang 68 - 74 Bài 10: Có thể đo gián tiếp chiều cao của một bức tường bằng dụng cụ đo đơn giản được không?

Hình 13: thể hiện cách đo chiều cao $AB$ của một bức tường bằng các dụng cụ đơn giản gồm:

Hai cọc thẳng đứng và sợi dây $FC$, Cọc 1 có chiều cao $DK=h$. Các khoảng cách $BC=a,DC=b$ đo được bằng thước thông dụng.

a) Em hãy cho biết người ta tiến hành đo đạc như thế nào ? 

b) Tính chiều cao $AB$ theo $h,a,b$.