Toptailieu.vn giới thiệu Vở bài tập Toán 8 trang 80, 81, 82, 83 Bài 4: Khái niệm hai tam giác đồng dạng chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong Vở bài tập Toán 8. Mời các bạn đón đọc.
Vở bài tập Toán trang 80, 81, 82, 83 Bài 4: Khái niệm hai tam giác đồng dạng
Câu hỏi Vở bài tập Toán 8 trang 80 - 83:
Câu 9
theo tỉ số . theo tỉ số bằng:
(A) (B) (C)
Khoanh tròn vào chữ cái đứng trước khẳng định đúng.
Phương pháp giải:
Tam giác theo tỉ số thì theo tỉ số .
Lời giải:
Tam giác theo tỉ số thì theo tỉ số .
Chọn C.
Câu 10
theo tỉ số , theo tỉ số . Khi đó theo tỉ số bằng:
A. B.
C. D.
Khoanh tròn vào chữ cái đứng trước khẳng định đúng.
Phương pháp giải:
theo tỉ số , theo tỉ số . Khi đó theo tỉ số .
Lời giải:
theo tỉ số , theo tỉ số .
Khi đó theo tỉ số .
Chọn B.
Câu 11
theo tỉ số , theo tỉ số (h.23). Khi đó theo tỉ số bằng:
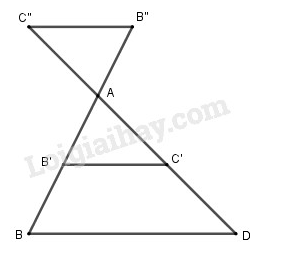
(A) (B) (C)
Khoanh tròn vào chữ cái đứng trước khẳng định đúng.
Phương pháp giải:
Sử dụng tính chất của tam giác đồng dạng:
- Tam giác theo tỉ số thì theo tỉ số .
- theo tỉ số , theo tỉ số . Khi đó theo tỉ số .
Lời giải :
theo tỉ số .
theo tỉ số theo tỉ
số
Khi đó theo tỉ số .
Chọn C.
Vở bài tập Toán 8 trang 80 - 83 Bài 16: Trong hai mệnh đề sau, mệnh đề nào đúng? Mệnh đề nào sai?
a) Hai tam giác bằng nhau thì đồng dạng với nhau.
b) Hai tam giác đồng dạng với nhau thì bằng nhau.
Phương pháp giải: Áp dụng định nghĩa hai tam giác đồng dạng, hai tam giác bằng nhau.
Lời giải:
a) Giả sử
Ta có:
Từ đó suy ra . Do đó
Vậy: mệnh đề a) là mệnh đề đúng.
b) Giả sử .
Khi đó
Nếu thì .
Nếu thì .
Do đó, mệnh đề b) là mệnh đề sai.
Vở bài tập Toán 8 trang 80 - 83 Bài 17: ∽theo tỉ số đồng dạng∽theo tỉ số đồng dạng. Hỏi tam giácđồng dạng với tam giáctheo tỉ số nào?
Phương pháp giải: Áp dụng tính chất: Nếu ∽và ∽ thì ∽
Lời giải:
∽ theo tỉ số đồng dạng , do đó ta có: (1)
∽ theo tỉ số đồng dạng , do đó ta có: (2)
Từ các đẳng thức (1) và (2) ta có:
Vậy theo tỉ số đồng dạng
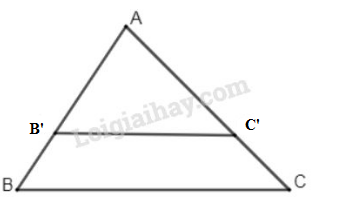
Vở bài tập Toán 8 trang 80 - 83 Bài 18: Cho tam giác . Hãy vẽ một tam giác đồng dạng với tam giác theo tỉ số .
Phương pháp giải: Áp dụng định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho.
Lời giải:
1. Cách dựng:
Trên cạnh , dựng điểm sao cho .
Trên cạnh , dựng điểm sao cho .
Tam giác là tam giác phải dựng (h.24).
2. Chứng minh:
Từ cách dựng ta có:
Áp dụng định lý Ta – let đảo, suy ra .
Áp dụng định lý bài 4, ta suy ra theo tỉ số
Vở bài tập Toán 8 trang 80 - 83 Bài 19:
∽ theo tỉ số đồng dạng .
a) Tính tỉ số chu vi của hai tam giác đã cho.
b) Cho biết chu vi của hai tam giác trên là dm, tính chu vi của mỗi tam giác.
Phương pháp giải:
Áp dụng:
- Tính chất hai tam giác đồng dạng.
- Tính chất của dãy tỉ số bằng nhau.
Lời giải:
a) ∽ theo tỉ số đồng dạng , do đó ta có:
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
hay
là chu vi của và là chu vi của .
Vậy tỉ số chu vi của và chính bằng tỉ số đồng dạng .
b) Ta có:
Áp dụng tính chất của tỉ lệ thức ta có:
Theo giả thiết ta có
Vậy
.
Vở bài tập Toán 8 trang 80 - 83 Bài 20: Cho tam giác vẽ tam giác đồng dạng với tam giác theo tỉ số đồng dạng là
Phương pháp giải: Áp dụng định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho.
Lời giải:
1. Cách dựng:
- Trên cạnh lấy điểm sao cho
- Trên cạnh lấy điểm sao cho
- Chọn ta được tam giác là tam giác cần dựng.
2. Chứng minh:
Từ cách dựng ta có: nên theo định lý Ta - let đảo ta có .
Theo định lý bài 4 ta suy ra ∽ theo tỉ số đồng dạng nên ∽ theo tỉ số đồng dạng .
Vở bài tập Toán 8 trang 80 - 83 Bài 21: Từ thuộc cạnh của tam giác với . Kẻ các tia song song với và , chúng cắt và lần lượt tại và
a) Nêu tất cả các cặp tam giác đồng dạng.
b) Đối với mỗi cặp tam giác đồng dạng, hãy viết các cặp góc bằng nhau và tỉ số đồng dạng tương ứng.
Phương pháp giải:
Áp dụng:
- Định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho.
- Tính chất hai tam giác đồng dạng
Lời giải:
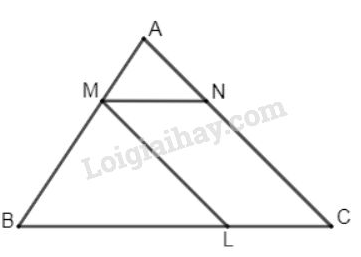
a) Áp dụng định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho, ta có:
(gt) ∽
(gt) ∽ .
và ∽ (vì cùng đồng dạng với tam giác )
b) ∽ có:
= ; = ; chung
Tỉ số đồng dạng (vì )
∽ có:
, chung,
Tỉ số đồng dạng
∽ có:
, ,
Tỉ số đồng dạng
