Vở bài tập Toán 8 trang 84, 85 Bài 5: Trường hợp đồng dạng thứ nhất (c.c.c)

Bạn cần đăng nhập để download tài liệu

Vở bài tập Toán 8 trang 84, 85 Bài 5: Trường hợp đồng dạng thứ nhất (c.c.c)

Dương Kiều Ninh Ngày: 26-05-2022 Lớp 8

358

Toptailieu.vn giới thiệu Vở bài tập Toán 8 trang 84, 85 Bài 5:Trường hợp đồng dạng thứ nhất (c.c.c) chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong Vở bài tập Toán 8. Mời các bạn đón đọc.

Vở bài tập Toán 8 trang 84, 85 Bài 5:Trường hợp đồng dạng thứ nhất (c.c.c)

Câu hỏi Vở bài tập Toán 8 trang 84, 85:

Câu 12.

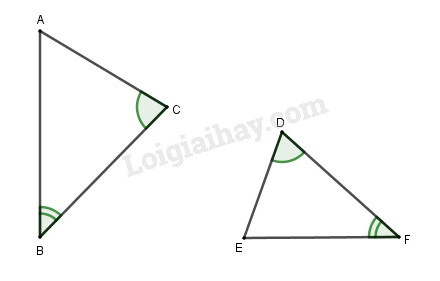
Trong hình vẽ 27 hai tam giác đồng dạng với nhau là:

A. $Δ A B C$ và $Δ D E F$

B. $Δ D E F$ và $Δ P M N$

C. $Δ P M N$ và $Δ A B C$

Khoanh tròn vào chữ cái trước khẳng định đúng.

Phương pháp giải:

Hai tam giác $A B C$ và $A^{'} B^{'} C^{'}$ đồng dạng nếu có $\frac{A B}{A^{'} B^{'}} = \frac{A C}{A^{'} C^{'}} = \frac{B C}{B^{'} C^{'}}$

Lời giải:

Ta thấy: $\frac{P M}{A B} = \frac{P N}{A C} = \frac{M N}{B C} = \frac{1}{2}$ nên $Δ P M N$ và $Δ A B C$ đồng dạng theo tỉ số $\frac{1}{2}$ .

Chọn C.

Câu 13.

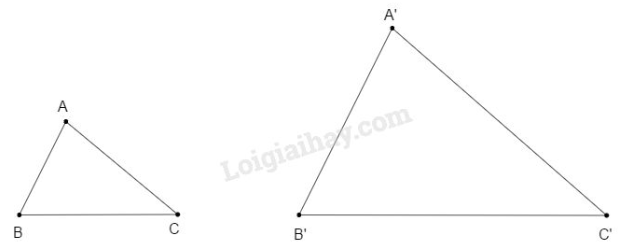
Trong hình $28$ cho biết hai tam giác đồng dạng với nhau. Hãy viết các góc tương ứng bằng nhau và các tỉ số bằng nhau vào chỗ trống

Phương pháp giải:

Sử dụng tính chất của tam giác đồng dạng:

Cho tam giác $Δ A B C ∽ Δ A^{'} B^{'} C^{'}$ .

Khi đó $\frac{A B}{A^{'} B^{'}} = \frac{A C}{A^{'} C^{'}} = \frac{B C}{B^{'} C^{'}};$ $\hat{A} = \hat{A^{'}}, \hat{B} = \hat{B^{'}}, \hat{C} = \hat{C^{'}}$

Lời giải: $\hat{A} = \hat{E} \hat{B} = \hat{F} \hat{C} = \hat{D}$

$\frac{A B}{E F} = \frac{A C}{D E} = \frac{B C}{D F}$

Vở bài tập Toán 8 trang 84, 85 Bài 22: Tam giác

A B C

có độ dài các cạnh là

A B = 3 c m, A C = 5 c m, B C = 7 c m

. Tam giác

A^{'} B^{'} C^{'}

đồng dạng với tam giác

A B C

và có chu vi bằng

55 c m

Hãy tính độ dài các cạnh của $A^{'} B^{'} C^{'}$ (làm tròn đến chữ số thập phân thứ hai)

Phương pháp giải: Áp dụng: Tính chất hai tam giác đồng dạng.

Lời giải:

$Δ A^{'} B^{'} C^{'} ∽ Δ A B C$ , do dó ta có:

$\frac{A^{'} B^{'}}{A B} = \frac{A^{'} C^{'}}{A C} = \frac{B^{'} C^{'}}{B C}$

hay $\frac{A^{'} B^{'}}{3}$ = $\frac{A^{'} C^{'}}{5}$ = $\frac{B^{'} C^{'}}{7}$

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

$\frac{A^{'} B^{'}}{3}$ = $\frac{A^{'} C^{'}}{5}$ = $\frac{B^{'} C^{'}}{7}$ $= \frac{A^{'} B^{'} + A^{'} C^{'} + B^{'} C^{'}}{3 + 5 + 7}$ = $\frac{55}{15}$

Từ đó ta tính được:

$A^{'} B^{'} = \frac{55}{15} .3 = 11, 00 c m$ ; $A^{'} C^{'} = \frac{55}{15} .5 \approx 18, 33 c m$

$B^{'} C^{'} = \frac{55}{15} .7 \approx 25, 67 c m$

Vở bài tập Toán 8 trang 84, 85 Bài 23: Cho hai tam giác đồng dạng có tỉ số chu vi là

\frac{15}{7}

và hiệu độ dài hai cạnh tương ứng của chúng là

12, 5 c m

. Tính hai cạnh đó.
Phương pháp giải:

Áp dụng:

- Tính chất của hai tam giác đồng dạng.

- Tính chất của dãy tỉ số bằng nhau.

Lời giải:

Giả sử $∆ A^{'} B^{'} C^{'}$ đồng dạng $∆ A B C$ , hiệu độ dài tương ứng của $A^{'} B^{'}$ và $A B$ là $12, 5 c m$ .

Vì $∆ A^{'} B^{'} C^{'}$ đồng dạng $∆ A B C$ (giả thiết) nên ta có:

$\frac{A^{'} B^{'}}{A B} = \frac{B^{'} C^{'}}{B C} = \frac{C^{'} A^{'}}{C A}$ $= \frac{A^{'} B^{'} + B^{'} C^{'} + C^{'} A^{'}}{A B + B C + C A}$ $= \frac{C_{A^{'} B^{'} C^{'}}}{C_{A B C}} = \frac{15}{17}$ (tính chất của dãy tỉ số bằng nhau).

(với $C_{A B C}$ và $C_{A^{'} B^{'} C^{'}}$ lần lượt là chu vi của hai tam giác $A B C, A^{'} B^{'} C^{'}$ )

Do đó, $\frac{A^{'} B^{'}}{A B} = \frac{15}{17}$

$\Rightarrow \frac{A B}{A^{'} B^{'}} = \frac{17}{15}$

$\begin{aligned} \Rightarrow \frac{A B}{A^{'} B^{'}} - 1 = \frac{17}{15} - 1 \\ \Rightarrow \frac{A B - A^{'} B^{'}}{A^{'} B^{'}} = \frac{17 - 15}{15} \\ \Rightarrow \frac{12, 5}{A^{'} B^{'}} = \frac{2}{15} \end{aligned}$