Toptailieu.vn giới thiệu Vở bài tập Toán 8 trang 77, 78, 79 Bài 3: Tính chất đường phân giác của tam giác chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong Vở bài tập Toán 8. Mời các bạn đón đọc.
Vở bài tập Toán 8 trang 77, 78, 79 Bài 3: Tính chất đường phân giác của tam giác
Câu hỏi Vở bài tập Toán 8 trang 77 - 79:
Câu 7. Cho biết . Hãy nhìn vào hình 16 rồi điền các tỉ số đúng vào những chỗ trống sau
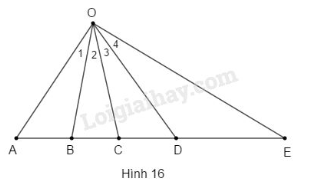
Phương pháp giải: Sử dụng:
- Định lí: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của hai đoạn ấy.
Lời giải:
Vì là tia phân giác của nên ta có: .
Vì là tia phân giác của nên ta có: .
Vì là tia phân giác của nên ta có: .
Vì là tia phân giác của nên ta có:
Câu 8. Cho biết (h.17).
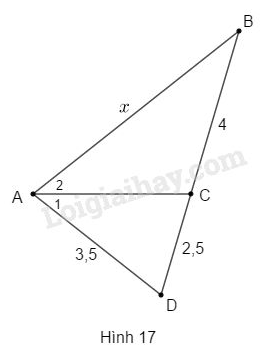
Độ dài của là:
(A) (B) (C) .
Khoanh tròn vào chữ cái trước khẳng định đúng.
Phương pháp giải: Sử dụng:
- Định lí: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của hai đoạn ấy
Lời giải:
Vì là tia phân giác của nên ta có:
Chọn C.
Vở bài tập Toán 8 trang 77 - 79 Bài 11: Tam giác có độ dài các cạnh , và là đường phân giác. Chứng minh rẳng tỉ số diện tích tam giác và diện tích tam giác bằng .
Phương pháp giải: Áp dụng: Công thức tính diện tích của tam giác, tính chất đường phân giác của tam giác.
Lời giải:
Lời giải:
Gọi diện tích của tam giác và (h.18) lần lượt là .
Gọi đường cao của tam giác là .
Vì là đường phân giác của góc , nên ta có:
(tính chất đường phân giác của tam giác)
Vậy (đpcm).
Vở bài tập Toán 8 trang 77 - 79 Bài 12: Cho tam giác với đường trung tuyến . Tia phân giác của góc cắt cạnh ở , tia phân giác của góc cắt cạnh ở . Chứng minh rằng (h.19)
Phương pháp giải: Áp dụng: Tính chất đường phân giác của tam giác, định lí TaLet đảo
Lời giải:
Ta có là đường phân giác góc của tam giác (giả thiết)
(1) (tính chất đường phân giác của tam giác)
là đường phân giác góc của tam giác (giả thiết)
(2) (tính chất đường phân giác của tam giác)
Mà (vì là đường trung tuyến nên là trung điểm cạnh)
(3)
Từ (1), (2), (3)
( theo định lí Talet đảo)
Vở bài tập Toán 8 trang 77 - 79 Bài 13: Cho hình thang ().
Đường thẳng song song với , cắt các cạnh và theo thứ tự là và
Chứng minh rằng:
a) ;
b)
c) .
Phương pháp giải: - Áp dụng tính chất của dãy tỉ số bằng nhau, định lí TaLet.
Lời giải:
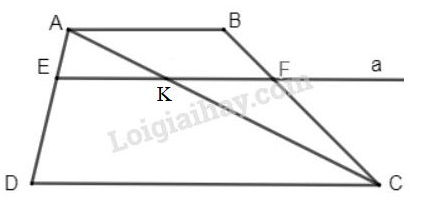
Vẽ thêm đường chéo , cắt tại (h.20)
+ Xét có (giả thiết)
Ta có: (1)
+ Xét có (giả thiết)
Ta có: (2)
Từ các tỉ lệ thức (1) và (2), ta suy ra: .
Tương tự như trên, xét có và có Ta có:
Suy ra .
Suy ra
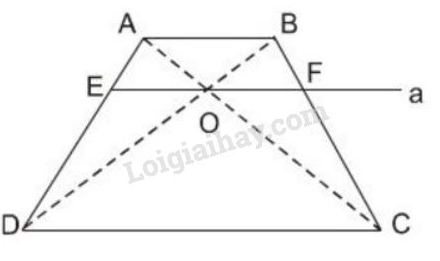
Vở bài tập Toán 8 trang 77 - 79 Bài 14: Cho hình thang . Hai đường chéo và cắt nhau tại . Đường thẳng qua và song song với đáy của hình thang cắt các cạnh theo thứ tự và (h26)
Chứng minh rằng .
Phương pháp giải:
- Áp dụng hệ quả của định lí TaLet trong tam giác.
- Áp dụng kết quả của bài 13b trang 77 VBT
Lời giải:
Xét có (gt) nên (1) (hệ quả của định lí TaLet trong tam giác)
Xét có (gt) nên (2) (hệ quả của định lí TaLet trong tam giác)
Mà (gt) nên (theo câu b bài 13 VBT trang 77) (3)
Từ (1), (2), (3) suy ra nên
Vở bài tập Toán 8 trang 77 - 79 Bài 15:
a) Cho tam giác với đường trung tuyến và đường phân giác . Tính diện tích tam giác , biết và diện tích của tam giác là .
b) Cho . Hỏi diện tích tam giác chiếm bao nhiêu phần trăm diện tích tam giác .
Phương pháp giải: Áp dụng: Tính chất đường phân giác trong tam giác. Trong một tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
Lời giải:
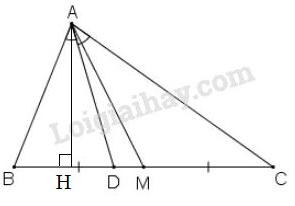
a) Từ tính chất của đường phân giác (h.22), ta có:
Từ tính chất của tỉ lệ thức, ta có:
hay
Rút gọn
Gọi là đường cao của .
b)
Vậy


