Toptailieu.vn giới thiệu Vở bài tập Toán 8 trang 86, 87, 88 Bài 6:Trường hợp đồng dạng thứ hai (c.g.c) chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong Vở bài tập Toán 8. Mời các bạn đón đọc.

Vở bài tập Toán 8 trang 86, 87, 88 Bài 6:Trường hợp đồng dạng thứ hai (c.g.c)

Câu hỏi Vở bài tập Toán 8 trang 86 - 88: Khoanh tròn vào chữ cái trước khẳng định đúng. Cho hình vẽ 29. 

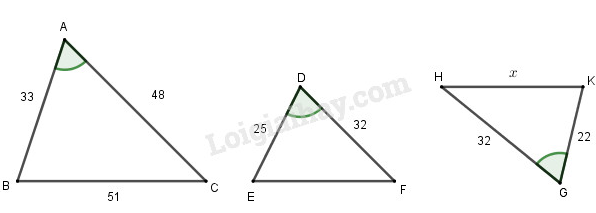
a,

Hai tam giác đồng dạng với nhau là:

A. $\mathrm{\Delta }ABC$ và $\mathrm{\Delta }DEF$

B. $\mathrm{\Delta }ABC$ và $\mathrm{\Delta }GKH$

C. $\mathrm{\Delta }GKH$ và $\mathrm{\Delta }DEF$

b,

Độ dài $x$ của cạnh $HK$ bằng:

A. $30$                             B. $31$

C. $33$                             D. $34$

Phương pháp giải:

a, Sử dụng dấu hiệu nhận biết hai tam giác đồng dạng theo trường hợp cạnh – góc - cạnh

b, Sử dụng tính chất hai tam giác đồng dạng
Lời giải:

a,

Xét $\mathrm{\Delta }ABC$ và $\mathrm{\Delta }GKH$ có:

${\displaystyle \frac{AB}{GK}}={\displaystyle \frac{AC}{GH}}={\displaystyle \frac{3}{2}}$

$\hat{A}=\hat{G}\left(gt\right)$

$\Rightarrow \mathrm{\Delta }ABC\backsim \mathrm{\Delta }GHK\left(c.g.c\right)$

Chọn B. 

b, Theo câu a) $\mathrm{\Delta }ABC\backsim \mathrm{\Delta }GKH$$\Rightarrow {\displaystyle \frac{AB}{GK}}={\displaystyle \frac{BC}{HK}}\Rightarrow {\displaystyle \frac{33}{22}}={\displaystyle \frac{51}{HK}}$ $\Rightarrow HK={\displaystyle \frac{22.51}{33}}=34$

Chọn D.

Vở bài tập Toán 8 trang 86 - 88 Bài 24: Chứng minh rằng nếu tam giác $A\text{'}B\text{'}C\text{'}$ đồng dạng với tam giác $ABC$ theo tỉ số , thì tỉ số của hai đường trung tuyến tương ứng với hai tam giác đó cũng bằng $k$.
Phương pháp giải:

Áp dụng:

- Định lí: Nếu hai cạnh tam giác này tỉ lệ với hai cạnh của tam giác kia và góc tạo bởi các cặp đó bằng nhau, thì hai tam giác đồng dạng.

- Tính chất hai tam giác đồng dạng.

- Tính chất trung tuyến.

Lời giải:

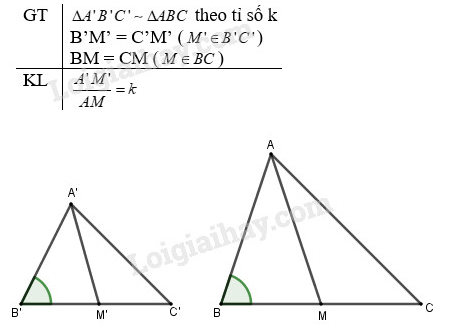
Từ giả thiết $\mathrm{\Delta }{A}^{\prime }{B}^{\prime }{C}^{\prime }\backsim \mathrm{\Delta }ABC$ theo tỉ số k (h.30) nên ta có:

$\widehat{A^{\prime }}=\hat{A};\widehat{B^{\prime }}=\hat{B};\widehat{C^{\prime }}=\hat{C};$ ${\displaystyle \frac{A^{\prime }{B}^{\prime }}{AB}}={\displaystyle \frac{A^{\prime }{C}^{\prime }}{AC}}={\displaystyle \frac{B^{\prime }{C}^{\prime }}{BC}}=k$

Xét hai tam giác $\mathrm{\Delta }{A}^{\prime }{B}^{\prime }{M}^{\prime }$ và $\mathrm{\Delta }ABM$:

${\displaystyle \frac{B^{\prime }{C}^{\prime }}{BC}}=k$ nên ${\displaystyle \frac{{\displaystyle \frac{1}{2}}{B}^{\prime }{C}^{\prime }}{{\displaystyle \frac{1}{2}}BC}}=k$ hay ${\displaystyle \frac{B^{\prime }{M}^{\prime }}{BM}}=k$ (1)

Mặt khác $\widehat{B^{\prime }}=\hat{B}$ và ${\displaystyle \frac{A^{\prime }{B}^{\prime }}{AB}}=k$ (2) (theo giả thiết)

Từ (1) và (2) suy ra ${\displaystyle \frac{A^{\prime }{B}^{\prime }}{AB}}={\displaystyle \frac{B^{\prime }{M}^{\prime }}{BM}}$

Theo định lý về trường hợp đồng dạng thứ hai, ta suy ra:

$\mathrm{\Delta }{A}^{\prime }{B}^{\prime }{M}^{\prime }\backsim \mathrm{\Delta }ABM$ $\Rightarrow {\displaystyle \frac{A^{\prime }{M}^{\prime }}{AM}}={\displaystyle \frac{A^{\prime }{B}^{\prime }}{AB}}=k$ (đpcm)

Vậy: nếu hai tam giác đồng dạng với nhau theo tỉ số $k$ thì tỉ số hai trung tuyến tương ứng cũng bằng $k$.

Vở bài tập Toán 8 trang 86 - 88 Bài 25: Trên một cạnh của góc $xOy$ ($\widehat{xOy}\ne {180}^0$), Đặt các đoạn thẳng $OA=5cm,OB=16cm$. Trên cạnh thứ hai của góc đó, đặt các đoạn $OC=8cm,OD=10cm$.

a) Chứng minh hai tam giác $OCB$ và $OAD$ đồng dạng.

b) Gọi giao điểm của các cạnh $AD$ và $BC$ là $I$, chứng minh rằng hai tam giác $IAB$ và $ICD$ có các góc bằng nhau từng đôi một.

Phương pháp giải:

Áp dụng:

- Định lí: Nếu hai cạnh tam giác này tỉ lệ với hai cạnh của tam giác kia và góc tạo bởi các cặp đó bằng nhau, thì hai tam giác đồng dạng.

- Định lí tổng ba góc trong một tam giác.

- Tính chất hai tam giác đồng dạng.

Lời giải:

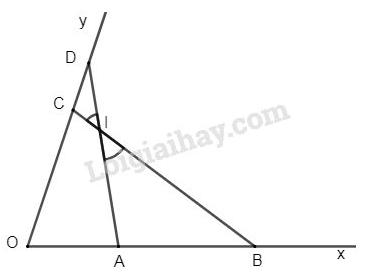
a) ${\displaystyle \frac{OA}{OC}}={\displaystyle \frac{5}{8}}$ ; ${\displaystyle \frac{OD}{OB}}={\displaystyle \frac{10}{16}}={\displaystyle \frac{5}{8}}$ 

$\Rightarrow {\displaystyle \frac{OA}{OC}}={\displaystyle \frac{OD}{OB}}$

Xét  $∆OCB$ và $∆OAD$ có:

+) $\hat{O}$ chung

+) ${\displaystyle \frac{OA}{OC}}={\displaystyle \frac{OD}{OB}}$ (chứng minh trên)

 $\Rightarrow ∆OCB$ đồng dạng $∆OAD$ ( c-g-c)

$\Rightarrow \widehat{ODA}=\widehat{CBO}$ (2 góc tương ứng) hay $\widehat{CDI}$ = $\widehat{IBA}$ 

b) $∆ICD$ và $∆IAB$ có

 $\widehat{CID}$ = $\widehat{AIB}$ (hai góc đối đỉnh)   (1)

$\widehat{CDI}$ = $\widehat{IBA}$ (theo câu a)            (2)

Theo định lí tổng ba góc trong một tam giác ta có:

$\begin{array}{rl}& \widehat{CID}+\widehat{CDI}+\widehat{ICD}={180}^0\\ & \widehat{AIB}+\widehat{IBA}+\widehat{IAB}={180}^0\end{array}$

$\Rightarrow \widehat{CID}+\widehat{CDI}+\widehat{ICD}$ $=\widehat{AIB}+\widehat{IBA}+\widehat{IAB}$   (3)

Từ (1), (2) và (3) suy ra: $\widehat{ICD}=\widehat{IAB}$

Vậy hai tam giác $IAB$ và $ICD$ có các góc bằng nhau từng đôi một.

Phương pháp giải:

Áp dụng định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho.

- Tính chất hai tam giác đồng dạng.

Lời giải:

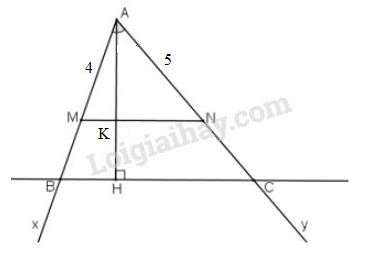
1. Phân tích:

Giả sử đã dựng được $\mathrm{\Delta }ABC$ có $\hat{A}={60}^0$, $AH=6cm$ và ${\displaystyle \frac{AB}{AC}}={\displaystyle \frac{4}{5}}$.

Trên tia $AB$ vẽ điểm $M$ sao cho $AM=4$ đơn vị dài.

Trên tia $AC$ vẽ điểm $N$ sao cho $AN=5$ đơn vị dài.

Ta có: ${\displaystyle \frac{AM}{AN}}={\displaystyle \frac{4}{5}}.$ Vậy ${\displaystyle \frac{AM}{AN}}={\displaystyle \frac{AB}{AC}}$ (vì cùng bằng ${\displaystyle \frac{4}{5}}$)

Suy ra ${\displaystyle \frac{AM}{AB}}={\displaystyle \frac{AN}{AC}}$.

Theo định lý Ta – let đảo, $MN//BC$. $AH\mathrm{\perp }BC$ nên $AH\mathrm{\perp }MN$ tại $K$.

Tam giác $AMN$ xác định thì tam giác $ABC$ cũng được xác định. Từ đó suy ra cách dựng như sau:

2. Cách dựng:

- Dựng góc $\widehat{xAy}={60}^0$

- Trên tia $Ax$ lấy điểm $M$ sao cho $AM=4$ đơn vị dài.

Trên tia $Ay$ lấy điểm $N$ sao cho $AN=4$ đơn vị dài.

Vẽ đoạn thẳng $MN$ được tam giác $AMN$ có $\hat{A}={60}^0$.

Vẽ đường cao $AK$ của tam giác $AMN$.

Trên tia $AK$ lấy điểm $H$ sao cho $AH=6cm$.

Qua $H$ dựng đường thẳng vuông góc với $AH$, đường thẳng này cắt tia $Ax$ tại $B$, cắt tia $Ay$ tại $C$. Tam giác $ABC$ là tam giác phải dựng. (h.31).

3. Chứng minh:

(Ta phải chứng minh $\mathrm{\Delta }ABC$ có đầy đủ các yêu cầu của bài toán).

$\mathrm{\Delta }ABC$ có góc $\hat{A}={60}^0$ (theo cách dựng) (1)

$\mathrm{\Delta }ABC$ có đường cao $AH=6cm$ (theo cách dựng) (2)

Mặt khác, $MN//BC$ vì $MN$ và $BC$ cùng vuông góc với $AH$)

Theo định lý Ta – let ta có: ${\displaystyle \frac{AM}{AB}}={\displaystyle \frac{AN}{AC}}$ $\Rightarrow {\displaystyle \frac{AB}{AC}}={\displaystyle \frac{AM}{AN}}={\displaystyle \frac{4}{5}}\left(3\right)$

Tam giác có đầy đủ ba điều kiện (1), (2), (3) theo yêu cầu của bài toán.

Vậy đó là tam giác phải dựng.