Toptailieu.vn giới thiệu Vở bài tập Toán 8 trang 96, 97, 98, 99, 100 Bài 8: Các trường hợp đồng dạng của tam giác vuông chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong Vở bài tập Toán 8. Mời các bạn đón đọc.
Vở bài tập Toán 8 trang 96, 97, 98, 99, 100 Bài 8: Các trường hợp đồng dạng của tam giác vuông
Câu hỏi Vở bài tập Toán 8 trang 96 - 100:
Câu 16
Tam giác vuông tại có , . Tam giác vuông tại có . Hai tam giác vuông và (h.41) đồng dạng với nhau nếu bằng:
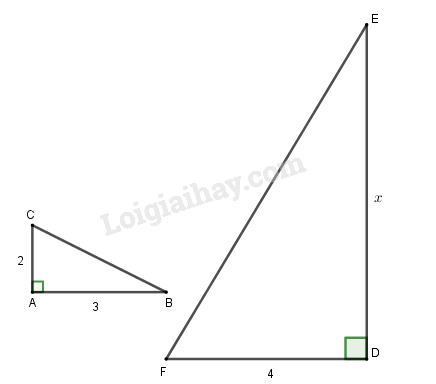
A. B.
C. D.
Khoanh tròn vào chữ cái đứng trước khẳng định đúng.
Phương pháp giải:
Xét hai tam giác đồng dạng, từ đó suy ra tỉ số các cạnh và tính .
Lời giải:
(tính chất tam giác đồng dạng)
.
Chọn C.
Câu 17
Cho ba tam giác vuông với kích thước các cạnh (cùng đơn vị đo) ghi trên hình 42.
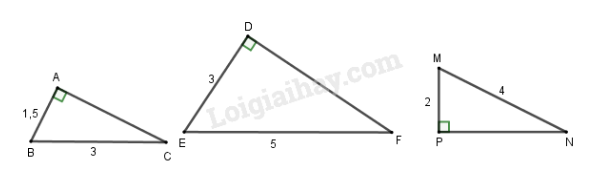
Hai tam giác đồng dạng với nhau là:
A. và
B. và
C. và
Phương pháp giải:
Tính độ dài cạnh còn lại của tam giác bằng định lí Pi – ta – go rồi sử dụng trường hợp đồng dạng của tam giác vuông để nhận xét.
Lời giải:
Tam giác vuông tại nên
Xét tam giác và có và nên hai tam giác không thể đồng dạng. Loại A.
Xét tam giác và có và nên hai tam giác không thể đồng dạng. Loại B.
Xét tam giác và có và nên
Chọn C.
Câu 18
Cho biết theo tỉ số đồng dạng , diện tích tam giác là: . Khi đó diện tích tam giác bằng:
A. B.
C.
Khoanh tròn vào chữ cái trước khẳng định đúng.
Phương pháp giải:
Sử dụng tính chất: Tỉ số diện tích của hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng.
Lời giải:
theo tỉ số đồng dạng
Chọn C.
Vở bài tập Toán 8 trang 96 - 100 Bài 35: Tam giác ABC có độ dài các cạnh là . Tam giác A'B'C' đồng dạng với tam giác ABC và có diện tích là
Tính độ dài cách cạnh của tam giác .
Phương pháp giải: - Áp dụng tính chất của hai tam giác đồng dạng, công thức tính diện tích tam giác.
Lời giải:
Ta nhận thấy
Suy ra là tam giác vuông có cạnh huyền là , hai cạnh góc vuông là và (giả sử ).
Diện tích tam giác là:
Vì theo tỉ số nên ta có:
hay (1)
Ta lại có (định lí 3 bài 8).
Từ (2) ta tính được
Từ (1) ta tính được
Đáp số:
Vở bài tập Toán 8 trang 96 - 100 Bài 36: Bóng của một cột điện trên mặt đất có độ dài là . Cùng thời điểm đó, một thanh sắt cao cắm vuông góc với mặt đất có bóng dài . Tính chiều cao của cột điện.
Phương pháp giải: Áp dụng tính chất hai tam giác đồng dạng.
Lời giải:
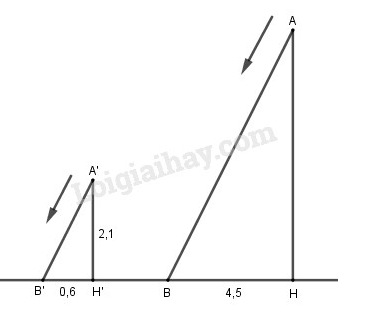
Gọi chiều cao của cột điện là , bóng dài của cột điện là thì phương chiếu của tia nắng xuống mặt đất là (h.43).
Gọi chiều cao của thanh sắt , bóng dài của thanh sắt thì phương chiếu của tia nắng xuống mặt đất là .
Xét hai tam giác và :
Vì cột điện và thanh sắt cùng vuông góc với mặt đất, do đó: và là hai tam giác vuông (;).
Vì góc hợp bởi tia nắng và mặt đất như nhau, nên ta có:
Suy ra
Do đó hay
Suy ra
Đáp số: Cột điện cao
Vở bài tập Toán 8 trang 96 - 100 Bài 37: Chân đường cao của tam giác vuông chia cạnh huyền thành hai đoạn có độ dài và . Tính chu vi và diện tích của tam giác vuông đó (h.45)
Phương pháp giải:
Hướng dẫn: Trước tiên tìm cạch từ các tam giác vuông đồng dạng, sau đó tính các cạnh của tam giác
Lời giải:
Xét hai tam giác vuông và
Suy ra
Do đó và ta có:
Xét hai tam giác vuông và có chung góc
Vậy .
Do đó
Tương tự xét hai tam giác vuông và có góc chung.
Vậy:
Do đó
Chu vi tam giác là:
Diện tích tam giác là:
.
Vở bài tập Toán 8 trang 96 - 100 Bài 38: Chân đường cao của tam giác vuông chia cạnh huyền thành hai đoạn có độ dài và . Tính chu vi và diện tích của tam giác vuông đó (h.45)
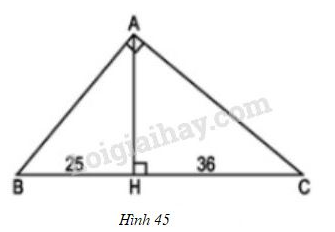
Phương pháp giải: Hướng dẫn: Trước tiên tìm cạch từ các tam giác vuông đồng dạng, sau đó tính các cạnh của tam giác
Lời giải:
Xét hai tam giác vuông và
Suy ra
Do đó và ta có:
Xét hai tam giác vuông và có chung góc
Vậy .
Do đó
Tương tự xét hai tam giác vuông và có góc chung.
Vậy:
Do đó
Chu vi tam giác là:
Diện tích tam giác là:
.
Vở bài tập Toán 8 trang 96 - 100 Bài 39: Cho một tam giác vuông, trong đó có cạnh huyền dài và một cạnh góc vuông dài . Tính độ dài hình chiếu cạnh góc vuông kia trên cạnh huyền.
Phương pháp giải: Áp dụng tính chất hai tam giác đồng dạng.
Lời giải:
Giả sử tam giác vuông tại có cạnh huyền , cạnh góc vuông .
Hạ đường cao , hình chiếu của trên cạnh huyền là . Ta phải tính độ dài của .
Xét hai tam giác vuông và có góc chung
Do đó .
Suy ra
Từ đó ta có .
Vở bài tập Toán 8 trang 96 - 100 Bài 40: Ở hình 47, tam giác vuông tại có đường cao
a) Trong hình vẽ có bao nhiêu cặp tam giác đồng dạng? (Hãy chỉ rõ từng cặp tam giác đồng đạng và viết theo các đỉnh tương ứng).
b) Cho biết: , . Tính độ dài các đoạn thẳng và
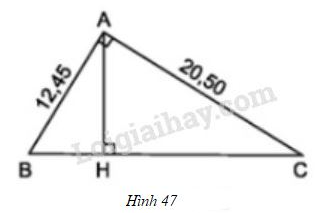
Phương pháp giải:
Áp dụng:
- Trường hợp đồng dạng: Tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia.
- Tính chất hai tam giác đồng dạng.
Lời giải:
a) Xét và có:
chung
(g-g)
Xét và có:
chung
(g-g)
b) vuông tại (giả thiết) nên áp dụng định lí Pitago ta có:
(chứng minh trên)
Mặt khác:
.


