Toptailieu.vn giới thiệu Vở bài tập Toán 8 trang 103, 104, 105, 106, 107 Bài 10: Ôn tập chương 3 – Tam giác đồng dạng chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong Vở bài tập Toán 8. Mời các bạn đón đọc.
Vở bài tập Toán 8 trang 103, 104, 105, 106, 107 Bài 10: Ôn tập chương 3 – Tam giác đồng dạng
Vở bài tập Toán 8 trang 103 - 107 Bài 44: Cho tam giác . Vẽ đường cao , đường phân giác , đường trung tuyến . Có nhận xét gì về vị trí của ba điểm .
Phương pháp giải: Áp dụng: Tính chất đường phân giác của tam giác, quan hệ giữa cạnh và góc trong tam giác.
Lời giải:
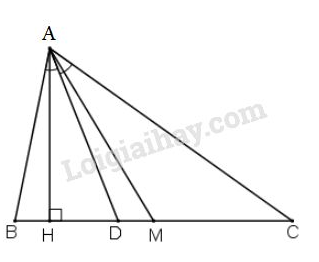
Khi vẽ đường cao , đường phân giác và đường trung tuyến (các điểm đều thuộc cạnh ), ta thấy rằng điểm luôn luôn nằm giữa hai điểm và (h.52). Nghĩa là đường phân giác luôn nằm giữa đường cao và đường trung tuyến. Ta có thể chứng minh được điều đó như sau:
Từ tính chất của đường phân giác, ta có
Vì (giả thiết), suy ra
hay .
Vậy điểm nằm bên trái điểm (1)
Mặt khác, ta lại có:
Vì (giả thiết) nên
Từ đó suy ra , nghĩa là
Vậy tia phải nằm giữa tia và và suy ra điểm phải nằm bên trái điểm (2)
Từ các kết luận (1) và (2) ta suy ra điểm luôn nằm giữa hai điểm và (đpcm).
Vở bài tập Toán 8 trang 103 - 107 Bài 45: Cho tam giác cân , vẽ các đường cao (h.53).
a) Chứng minh .
b) Chứng minh .
c) Cho biết . Tính độ dài đoạn thẳng .
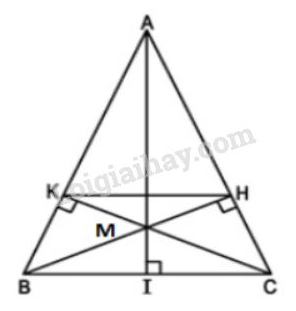
Phương pháp giải:
Hướng dẫn câu c):
- Vẽ thêm đường cao , xét hai tam giác đồng dạng và rồi tính .
- Tiếp theo, xét hai tam giác đồng dạng và rồi tính .
Lời giải:
a) Xét hai tam giác vuông và , ta có (vì )
là cạnh huyền chung.
Suy ra
b) Từ giả thiết và (theo chứng minh trên) suy ra , ta có
c) Vẽ thêm đường cao ; đồng quy tại .
(vì , góc chung).
Suy ra hay
Từ suy ra
Vở bài tập Toán 8 trang 103 - 107 Bài 46: Hình thang có và cắt nhau tại và cắt nhau tại . Chứng minh rằng đi qua trung điểm của các cạnh và .
Phương pháp giải:
- Qua kẻ đường thẳng song song với cắt lần lượt tại .
- Chứng minh .
- Chứng minh
Lời giải:
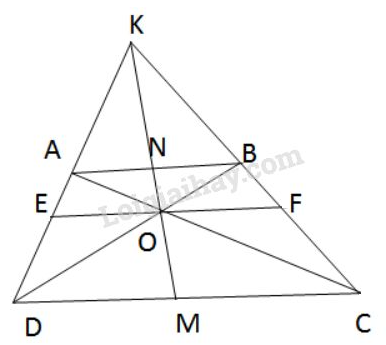
Qua kẻ (h.54)
Trước hết hãy chứng minh rằng .
Xét có nên ta có:
(1)
Xét có nên ta có:
(2)
Vì nên ta có:
(3)
Từ các đẳng thức (1), (2) và (3) suy ra (4)
Từ , ta có:
và suy ra (vì ).
Vậy là trung điểm của .
Tương tự như vậy, từ , ta có:
và ; suy ra (vì ).
Vậy là trung điểm của .
Vở bài tập Toán 8 trang 103 - 107 Bài 47: Cho tam giác vuông , và đường phân giác ( thuộc cạnh ).
a) Tính tỉ số .
b) Cho biết độ dài . Hãy tính chu vi và diện tích của tam giác
Phương pháp giải: Áp dụng: Tính chất đường phân giác của tam giác, định lí Pitago, công thức tính chu vi và diện tích của tam giác.
Lời giải:
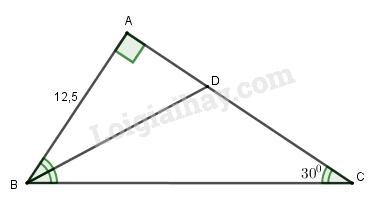
a) Vì , , suy ra .
là đường phân giác (h.55), do đó ta có:
b)
Gọi và lần lượt là chu vi và diện tích của tam giác ta có:
.
Vở bài tập Toán 8 trang 103 - 107 Bài 48: Tứ giác có , , đường chéo .
a) Nêu cách vẽ tứ giác có kích thước đã cho ở trên.
b) Các tam giác và có đồng dạng với nhau không? Vì sao?
c) Chứng minh rằng .
Phương pháp giải: Áp dụng cách vẽ tam giác, dấu hiệu nhận biết hình thang, dấu hiệu nhận biết hai tam giác đồng dạng.
Lời giải:
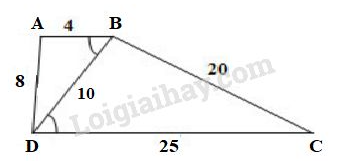
a) Để vẽ được tứ giác , trước hết ta phải xác định được các đỉnh của nó, sau đó vẽ các cạnh. Cách vẽ như sau:
- Vẽ (h.56), xác định được hai đỉnh và cạnh .
- Lấy và làm tâm, thứ tự quay hai cung tròn cắt nhau có bán kính là và , xác định được đỉnh .
- Lấy và làm tâm, thứ tự quay hai cung tròn cắt nhau có bán kính là và , xác định được đỉnh .
- Vẽ các đoạn thẳng được tứ giác thỏa mãn các yêu cầu của bài toán.
b) Xét hai tam giác và , ta thấy:
;
Do đó (c.c.c)
c) Hai tam giác và đồng dạng với nhau do đó các góc tương ứng phải bằng nhau.
(hai góc so le trong bằng nhau).
Đề kiểm tra 45 phút chương 3 phần Hình học 8 - Đề số 1:
Câu 1:
Hãy chọn kết quả đúng. Tam giác vuông tại có độ dài , đường cao (h.57)
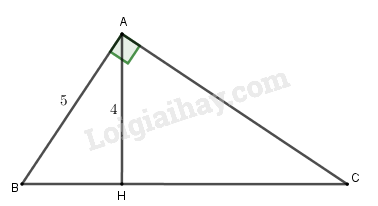
a) Độ dài của là:
A.
B.
C.
D.
b) Độ dài của là:
A.
B.
C.
D.
c) Độ dài của là:
A.
B.
C.
D.
Câu 2. (7 điểm) Cho hình thang vuông có , cạnh vuông góc với đường chéo , đường phân giác của góc cắt cạnh tại . Cho biết độ dài và góc (h.58)
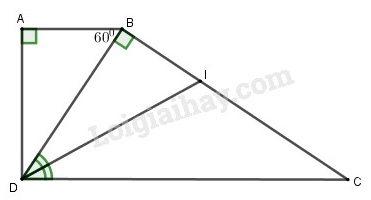
a) Chứng minh rằng là tam giác cân.
b) Tính độ dài của các cạnh và độ dài của phân giác .
Lời giải:
Câu 1:
Phương pháp:
Sử dụng định lý Pi – ta – go trong tam giác vuông và tam giác đồng dạng để tính độ dài các cạnh.
Cách giải:
a) Tam giác vuông tại nên .
Chọn C.
b) Xét tam giác và có:
(cùng phụ với góc )
Chọn C.
c) Ta có:
Áp dụng định lí Pi – ta – go cho tam giác vuông có:
Chọn A.
Câu 2:
Phương pháp:
a) Chứng minh tam giác có hai góc và suy ra .
b) Sử dụng các tam giác đồng dạng và định lí Pi – ta – go để tính toán.
Chú ý kết quả: Tam giác vuông có một góc bằng thì cạnh đối cửa góc bằng nửa cạnh huyền.
Cách giải:
a) Tam giác vuông tại có:
(hai góc nhọn trong tam giác vuông)
(1)
Tam giác vuông tại có (hai góc nhọn trong tam giác vuông)
hay (2)
Từ (1) và (2) suy ra nên tam giác cân tại
(đpcm).
b) Tam giác vuông tại có nên
Áp dụng định lí Pi – ta – go ta có:
Tam giác vuông tại có nên
Áp dụng định lí Pi – ta – go ta có:
.
Ta có:
Mà
Áp dụng định lí Pi – ta – go ta có:
.
Đề kiểm tra 45 phút chương 3 phần Hình học 8 - Đề số 2:
Câu 1. (3 điểm) Hãy chọn kết quả đúng. Tam giác có đường phân giác . Cho biết độ dài . (h.59)
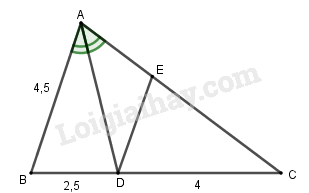
a) Độ dài của cạnh là:
A.
B.
C.
D.
b) Từ kẻ . Độ dài của đoạn thẳng là:
A.
B.
C.
D.
c) Độ dài của đoạn thẳng là:
a) Độ dài của cạnh là:
A.
B.
C.
D.
b) Từ kẻ . Độ dài của đoạn thẳng là:
A.
B.
C.
D.
c) Độ dài của đoạn thẳng là:
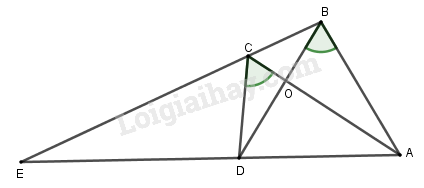
Chứng minh rằng:
a)
b)
c)
Lời giải:
Câu 1:
Phương pháp:
a) Sử dụng tính chất đường phân giác của tam giác.
b) Sử dụng hệ quả của định lí Ta – let.
c) Sử dụng hệ quả của định lí Ta – let và các kết quả tính được ở trên.
Cách giải:
a) là phân giác của nên .
Chọn B.
b) nên theo hệ quả của định lý Ta – let ta có:
.
Chọn A.
c) nên theo hệ quả của định lý Ta – let ta có:
Chọn B.
Câu 2:
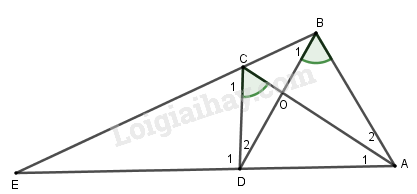
Phương pháp:
a) Sử dụng trường hợp đồng dạng góc – góc.
b) Sử dụng trường hợp đồng dạng cạnh – góc – cạnh.
c) Chứng minh hai tam giác đồng dạng tam giác và kết luận.
Cách giải:
a) Xét và có:
(đối đỉnh)
(đpcm).
b) Từ câu a,
xét và có:
(đối đỉnh)
(đpcm).
c) Ta có:
là góc ngoài của tam giác nên (tính chất) (1)
Theo câu a) (góc tương ứng) (2)
Theo câu b) (góc tương ứng) (3)
Từ (1), (2) và (3) suy ra
Xét tam giác và tam giác có:
chung
.




