Với giải Câu hỏi trang 68 Toán 10 Tập 2 Kết nối tri thức chi tiết trong Bài tập cuối chương 9 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem: 

SBT Toán 10 Kết nối tri thức trang 68: Bài tập cuối chương 9

Bài 9.17 trang 68 Sách bài tập Toán lớp 10 Tập 2: Chọn ngẫu nhiên 5 học sinh trong một danh sách được đánh số thứ tự từ 1 đến 199.

a) Xác suất để cả 5 học sinh được chọn có số thứ tự nhỏ hơn 100 xấp xỉ là

A. 0,028;

B. 0,029;

C. 0,027;

D. 0,026.

b) Xác suất để cả 5 học sinh được chọn có số thứ tự lớn hơn 149 xấp xỉ là

A. 0,00089;

B. 0,00083;

C. 0,00088;

D. 0,00086.

Lời giải:

Đáp án đúng là: (a) B; (b) D

Chọn ngẫu nhiên 5 học sinh trong một danh sách được đánh số thứ tự từ 1 đến 199 có số cách là: $C_{199}^5=2472258789$.

Do đó, n(Ω) = 2 472 258 789.

a)

Số cách chọn 5 học sinh được chọn có số thứ tự nhỏ hơn 100 là: $C_{99}^5$ = 71 523 144.

Biến cố E: “5 học sinh được chọn có số thứ tự nhỏ hơn 100”. Ta có:

n(E) = 71 523 144

Vậy P(E) = $\frac{n\left(E\right)}{n\left(\Omega \right)}=\frac{71523144}{2472258789}\approx 0,029$.

b)

Ta có 5 học sinh được chọn có số thứ tự lớn hơn 149, có nghĩa là chọn 5 học sinh trong các học sinh có số thứ tự từ 150 đến 199, có tất cả (199 – 150) + 1 = 50 (học sinh).

Số cách chọn 5 học sinh được chọn có số thứ tự lớn hơn 149 là: $C_{50}^5$ = 2 118 760.

Biến cố F: “5 học sinh được chọn có số thứ tự lớn hơn 149”. Ta có:

n(F) = 2 118 760.

Vậy P(F) = $\frac{n\left(F\right)}{n\left(\Omega \right)}=\frac{2118760}{2472258789}\approx 0,00086$.

Bài 9.18 trang 68 Sách bài tập Toán lớp 10 Tập 2: Một túi đựng 3 viên bi trắng và 5 viên bi đen. Chọn ngẫu nhiên 3 viên bi. Xác suất để trong 3 viên bi đó có cả bi trắng và bi đen là

A. $\frac{13}{15}$;

B. $\frac{9}{11}$;

C. $\frac{43}{56}$;

D. $\frac{45}{56}$.

Lời giải:

Đáp án đúng là: D

Chọn ngẫu nhiên 3 viên bi trong số 8 viên bi có số cách là: $C_8^3=56$.

Do đó, n(Ω) = 56.

Gọi biến cố A: “3 viên bi đó có cả bi trắng và bi đen”.

Biến cố đối của A là 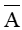: “3 viên bi đó chỉ có bi trắng hoặc chỉ có bi đen”

Số cách chọn 3 viên bi chỉ có bi trắng là: $C_3^3=1$

Số cách chọn 3 viên bi chỉ có bi đen là: $C_5^3=10$

Do đó, n() = 1 + 10 = 11

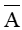
Vậy 

Bài 9.19 trang 68 Sách bài tập Toán lớp 10 Tập 2: Mũi tên của bánh xe trong trò chơi “Chiếc nón kì diệu” có thể dừng lại ở một trong 7 vị trí. Người chơi được quay 3 lần. Xác suất để mũi tên dừng lại ở ba vị trí khác nhau là

A. $\frac{30}{49}$;

B. $\frac{29}{50}$;

C. $\frac{3}{5}$;

D. $\frac{7}{11}$.

Lời giải:

Đáp án đúng là: A

Quay ngẫu nhiên 3 lần, mỗi lần có thể dừng lại ở một trong 7 vị trí.

Do đó, n(Ω) = 7 . 7 . 7 = 343.

Gọi biến cố A: “mũi tên dừng lại ở ba vị trí khác nhau trong 3 lần quay”.

Lần quay thứ nhất có số cách chọn vị trí là: 7

Lần quay thứ hai có số cách chọn vị trí là: 6

Lần quay thứ ba có số cách chọn vị trí là: 5

Số cách để mũi tên dừng lại ở ba vị trí khác nhau là: 7 . 6 . 5 = 210 (cách)

Do đó, n(A) = 210.

Vậy P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{210}{343}=\frac{30}{49}$.

Bài 9.20 trang 68 Sách bài tập Toán lớp 10 Tập 2: Gieo đồng thời hai con xúc xắc cân đối. Xác suất để số chấm xuất hiện trên hai con xúc xắc hơn kém nhau 2 là

A. $\frac{5}{22}$;

B. $\frac{1}{5}$;

C. $\frac{2}{9}$;

D. $\frac{7}{34}$.

Lời giải:

Đáp án đúng là: C

Không gian mẫu là: Ω = {(1, 1); (1, 2); (1, 3); (1, 4); (1, 5); (1, 6); (2, 1); (2, 2); (2, 3); (2, 4); (2, 5); (2, 6); (3, 1); (3, 2); (3, 3); (3, 4); (3, 5); (3, 6); (4, 1); (4, 2); (4, 3); (4, 4); (4, 5); (4, 6); (5, 1); (5, 2); (5, 3); (5, 4); (5, 5); (5, 6); (6, 1); (6, 2); (6, 3); (6, 4); (6, 5); (6, 6)}.

Suy ra n(Ω) = 36.

Biến cố A: “số chấm xuất hiện trên hai con xúc xắc hơn kém nhau 2”.

A = (1, 3); (2, 4); (3, 5); (4, 2); (5, 3); (6, 4); (3, 1); (4, 6)}.

Suy ra n(A) = 8.

Vậy P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{8}{36}=\frac{2}{9}$.

Bài 9.21 trang 68 Sách bài tập Toán lớp 10 Tập 2: Chọn ngẫu nhiên hai số từ tập hợp S = {1; 2; ...;19} rồi nhân hai số đó với nhau. Xác suất để kết quả là một số lẻ là

A. $\frac{9}{19}$;

B. $\frac{10}{19}$;

C. $\frac{4}{19}$;

D. $\frac{5}{19}$.

Lời giải:

Đáp án đúng là: D

Số cách chọn ngẫu nhiên hai số từ tập S là: $C_{19}^2$ = 171.

Do đó, n(Ω) = 171.

Biến cố A: “nhân hai số đó với nhau có kết quả là một số lẻ”

Để hai số nhân với nhau có kết quả là một số lẻ thì hai số đều phải là số lẻ. Trong tập S có 10 số lẻ. Vậy số cách chọn hai số lẻ là: $C_{10}^2$ = 45, do đó, n(A) = 45.

Vậy P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{45}{171}=\frac{5}{19}$.

Bài 9.22 trang 68 Sách bài tập Toán lớp 10 Tập 2: Gieo ba con xúc xắc cân đối và đồng chất. Xác suất để số chấm xuất hiện trên mặt của ba con xúc xắc khác nhau là

A. $\frac{5}{9}$;

B. $\frac{4}{9}$;

C. $\frac{7}{9}$;

D. $\frac{2}{9}$.

Lời giải:

Đáp án đúng là: A

Số kết quả khi gieo ba con xúc xắc cân đối và đồng chất là: 6 . 6 . 6 = 216.

Do đó, n(Ω) = 216.

Biến cố A: “số chấm xuất hiện trên mặt của ba con xúc xắc khác nhau”.

Số chấm trên con xúc xắc thứ nhất có số cách chọn là: 6

Số chấm trên con xúc xắc thứ hai có số cách chọn là: 5

Số chấm trên con xúc xắc thứ ba có số cách chọn là: 4

Theo quy tắc nhân, số cách gieo để số chấm xuất hiện trên mặt của ba con xúc xắc khác nhau là: 6 . 5 . 4 = 120.

Do đó, n(A) = 120.

Vậy P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{120}{216}=\frac{5}{9}$.

Bài 9.23 trang 68 Sách bài tập Toán lớp 10 Tập 2: Một khách sạn có 6 phòng đơn. Có 10 khách thuê phòng trong đó có 6 nam và 4 nữ. Người quản lí chọn ngẫu nhiên 6 người cho nhận phòng.

a) Xác suất để cả 6 người là nam là

A. $\frac{11}{210}$;

B. $\frac{1}{105}$;

C. $\frac{1}{210}$;

D. $\frac{7}{210}$.

b) Xác suất để có 4 nam và 2 nữ là

A. $\frac{2}{7}$;

B. $\frac{3}{7}$;

C. $\frac{4}{7}$;

D. $\frac{5}{7}$.

c) Xác suất để có ít nhất 3 nữ là

A. $\frac{17}{42}$;

B. $\frac{23}{42}$;

C. $\frac{25}{42}$;

D. $\frac{19}{42}$.

Lời giải:

Đáp án đúng là: (a) C; (b) B; (c) D

Chọn 6 người trong 10 người có số cách là: $C_{10}^6$ = 210.

Do đó, n(Ω) = 210.

a)

Biến cố A: “6 người là nam”. Ta có:

Để chọn 6 người là nam có số cách là: $C_6^6$ = 1

Do đó, n(A) = 1.

Vậy P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{1}{210}$.

b)

Biến cố B: “4 nam và 2 nữ”

Số cách chọn 4 nam là: $C_6^4$ = 15

Số cách chọn 2 nữ là: $C_4^2$ = 6

Do đó, theo quy tắc nhân, n(B) = 15 . 6 = 90.

Vậy P(B) = $\frac{n\left(B\right)}{n\left(\Omega \right)}=\frac{90}{210}=\frac{3}{7}$.

c)

Biến cố C: “có ít nhất 3 nữ”.

TH1: Có 3 bạn nữ, 3 bạn nam

Số cách chọn 3 bạn nữ là: $C_4^3$ = 4

Số cách chọn 3 bạn nam là: $C_6^3$ = 20

Số cách chọn 3 bạn nữ, 3 bạn nam là: 4 . 20 = 80.

TH2: Có 4 bạn nữ, 2 bạn nam

Số cách chọn 4 bạn nữ là: $C_4^4$ = 1

Số cách chọn 2 bạn nam là: $C_6^2$ = 15

Số cách chọn 4 bạn nữ, 2 bạn nam là: 1 . 15 = 15.

Theo quy tắc cộng, số cách chọn để có ít nhất 3 nữ là: 80 + 15 = 95, do đó, n(C) = 95.

Vậy P(C) = $\frac{n\left(C\right)}{n\left(\Omega \right)}=\frac{95}{210}=\frac{19}{42}$.