Với giải Câu hỏi trang 85 Toán 10 Tập 2 Chân trời sáng tạo trong Bài 2: Xác suất của biến cố học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Toán 10 Chân trời sáng tạo trang 85 Bài 2: Xác suất của biến cố
a) “Xuất hiện ba mặt sấp”
b) “Xuất hiện ít nhất một mặt sấp”
Lời giải
a) Biến cố đối của biến cố “Xuất hiện ba mặt sấp” là biến cố: “Xuất hiện ba mặt ngửa”
b) Biến cố đối của biến cố “Xuất hiện ít nhất một mặt sấp” là biến cố “Không xuất hiện mặt sấp nào”.
a) “Tổng số chấm xuất hiện nhỏ hơn 10”
b) “Tích số chấm xuất hiện chia hết cho 3”
Phương pháp giải
Bước 1: Xác định không gian mẫu
Bước 2: Xác định biến cố đối
Bước 3: Tính xác suất của biến cố đối bằng công thức
Bước 4: Xác định xác suất của biến cố ban đầu
Lời giải
Tổng số kết quả có thể xảy ra của phép thử là
a) Gọi biến cố A “Tổng số chấm xuất hiện lớn hơn hoặc bằng 10” là biến cố đối của biến cố “Tổng số chấm xuất hiện nhỏ hơn 10”
A xảy ra khi số chấm xuất hiện là 5 hoặc 6. Số kết quả thuận lợi cho A là
Xác suất của biến cố A là
Vậy xác suất của biến cố “Tổng số chấm xuất hiện nhỏ hơn 10” là
b) Gọi biến cố A: “Tích số chấm xuất hiện không chia hết cho 3” là biến cố đối của biến cố ‘“Tích số chấm xuất hiện chia hết cho 3”
A xảy ra khi mặt xuất hiện trên hai con xúc xắc đều xuất hiện số chấm không chia hết cho 3. Số kết quả thuận lợi cho A là:
Xác suất của biến cố A là:
Vậy xác suất của biến cố “Tích số chấm xuất hiện chia hết cho 3” là .
a) Sử dụng sơ đồ hình cây, hãy liệt kê tất cả các kết quả có thể xảy ra
b) Tính xác suất của biến cố “Trong 2 thẻ lấy ra có ít nhất 2 thẻ màu đỏ”
Lời giải
a) Các kết quả có thể xảy ra trong 2 lần lấy tấm thẻ từ 2 hộp được thể hiện ở sơ đồ hình cây như hình dưới đây:
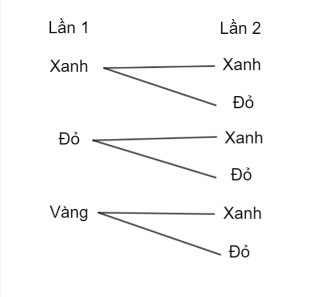
b)
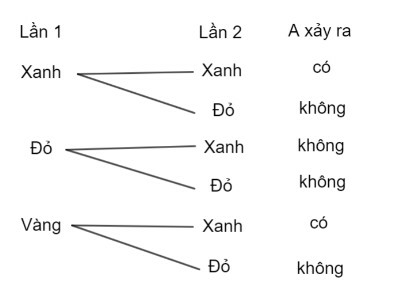
Gọi A là biến cố “Trong 2 thẻ lấy ra không có thẻ màu đỏ nào” là biến cố đối của biến cố “Trong 2 thẻ lấy ra có ít nhất 2 thẻ màu đỏ”
Dựa vào sơ đồ hình cây ta thấy có tất cả 6 kết quả có thể xảy ra, trong đó có 2 kết quả thuận lợi cho I. Do đó:
Vậy xác suất của biến cố “Trong 2 thẻ lấy ra có ít nhất 2 thẻ màu đỏ” là .

Lời giải
Ta thấy hai biến cố :”Hai quả bóng lây ra cùng màu” và “Hai quả bóng lấy ra khác màu” là hai biến cố đối
Suy ra xác suất của biến cố “Hai quả bóng lây ra cùng màu” là .
a) “Nhân và Tín không đứng cạnh nhau”
b) “Trí không đứng ở đầu hàng”
Phương pháp giải
Bước 1: Xác định không gian mẫu
Bước 2: Xác định biến cố đối
Bước 3: Tính xác suất của biến cố đối bằng công thức
Bước 4:Xác định xác suất của biến cố ban đầu
Lời giải
Tổng số kết quả có thể xảy ra của phép thử là
a) Gọi biến cố A “Nhân và Tín đứng cạnh nhau” là biến cố đối của biến cố “Nhân và Tín không đứng cạnh nhau”
Số kết quả thuận lợi cho A là:
Xác suất của biến cố A là:
Vậy xác suất của biến cố “Nhân và Tín không đứng cạnh nhau” là
b) Gọi biến cố A “Trí đứng ở đầu hàng” là biến cố đối của biến cố “Trí không đứng ở đầu hàng”
Số kết quả thuận lợi cho A là:
Xác suất của biến cố A là:
Vậy xác suất của biến cố “Nhân và Tín không đứng cạnh nhau” là .
Xem thêm các bài giải Toán 10 Chân trời sáng tạo hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.