Với giải Câu hỏi trang 56 Toán 10 Tập 2 Kết nối tri thức trong Bài 22: Ba đường Conic học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem: 

Toán 10 Kết nối tri thức trang 56 Bài 22: Ba đường Conic

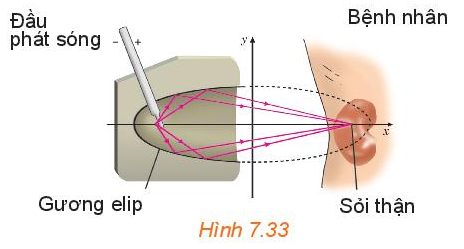
Vận dụng 3 trang 56 SGK Toán 10 Tập 2: Gương elip trong một máy tán sỏi thận (H7.33) ứng với clip có phương trình chính tắc là $\frac{x^2}{400}+\frac{y^2}{76}=1$  (theo đơn vị cm). Tính khoảng cách từ vị trí đầu phát sóng của máy đến vị trí của sỏi thận cần tán.

Lời giải:

Vị tri bắt đầu phát sóng của máy và vị trí viên sỏi được đặt ở hai tiêu điểm của gương elip, do đó khoảng cách cần tìm là tiêu cự của gương và bằng $2c=2\sqrt{400-76}=36\left(cm\right)$.

Bài tập

Bài 7.19 trang 56 SGK Toán 10 Tập 2: Cho Elip có phương trình $\frac{x^2}{36}+\frac{y^2}{9}=1$. Tìm tiêu điểm và tiêu cự của elip.

Phương pháp giải:

Tính $c=\sqrt{a^2-b^2}$,

+ Tiêu điểm: $F_1\left(-c;0\right),F_2\left(c;0\right)$

+ Tiêu cự: $F_1{F}_2=2c$.

Lời giải:

Ta có: $a^2=36,b^2=9\Rightarrow c=\sqrt{36-9}=3\sqrt{3}$ nên elip có hai tiêu điểm là $F_1\left(-3\sqrt{3};0\right);F_2\left(3\sqrt{3};0\right)$ và tiêu cự là $F_1{F}_2=2c=6\sqrt{3}$.

Bài 7.20 trang 56 SGK Toán 10 Tập 2: Cho hyperbol có phương trình $\frac{x^2}{7}-\frac{y^2}{9}=1$. Tìm tiêu điểm và tiêu cự của hyperbol.

Phương pháp giải:

Tính $c=\sqrt{a^2+b^2}$, 

+ tiêu điểm $F_1\left(-c;0\right),F_2\left(c;0\right)$

+ tiêu cự $F_1{F}_2=2c$.

Lời giải:

Ta có: $a^2=7,b^2=9\Rightarrow c=\sqrt{7+9}=4$ nên elip có hai tiêu điểm là $F_1\left(-4;0\right);F_2\left(4;0\right)$ và tiêu cự là $F_1{F}_2=2c=8$.

Bài 7.21 trang 56 SGK Toán 10 Tập 2: Cho parabol có phương trình $y^2=8x$. Tìm tiêu điểm và đường chuẩn của parabol.

Phương pháp giải:

Tìm p, sau đó dựa vào công thức xác định tiêu điểm  và đường chuẩn là  để kết luận.

Lời giải:

Ta có: $2p=8\Rightarrow p=4$ nên (P) có tiêu điểm là $F\left(2;0\right)$ và đường chuẩn là $x=-2$.

Bài 7.22 trang 56 SGK Toán 10 Tập 2: Lập phương trình chính tắc của elip đi qua hai điểm $A\left(5;0\right)$ và có một tiêu điểm là $F_2\left(3;0\right)$.

Phương pháp giải:

Gọi phương trình chính tắc của (E), sau đó thay tọa điểm A vào phương trình (E) và sử dụng  để tìm a,b.

Lời giải:

Phương trình chính tắc của elip có dạng: $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\left(a>b>0\right)$.

Elip đi qua $A\left(5;0\right)$ nên ta có $\frac{5^2}{a^2}+\frac{0^2}{b^2}=1\iff a^2=25$

Mặt khác elip có một tiêu điểm $F_2=\left(3;0\right)$ nên ta có $c=3$, suy ra $b^2=c^2-a^2=25-3^2=16$

Vậy phương trình của elip là: $\frac{x^2}{25}+\frac{y^2}{16}=1$.

Bài 7.23 trang 56 SGK Toán 10 Tập 2: Lập phương trình chính tắc của parabol đi qua điểm $M\left(2;4\right)$.

Phương pháp giải:

Gọi phương trình chính tắc của (P), sau đó thay tọa điểm M vào phương trình (P) để tìm được tham số tiêu p.

Lời giải:

Phương trình chính tắc của (P) có dạng $y^2=2px\left(p>0\right)$

Vì (P) đi qua điểm $M\left(2;4\right)$ nên ta có $4^2=2p.2\iff p=4$.

Vậy phương trình chính tắc của (P) là $y^2=8x$.

Bài 7.24 trang 56 SGK Toán 10 Tập 2: Có hai trạm phát tín hiệu vô tuyến đặt tại hai vị trí A, B cách nhau 300 km. Tại cùng một thời điểm, hai trạm cùng phát tín hiệu với vận tốc 292 000 km/s để một tàu thuỷ thu và đo độ lệch thời gian. Tín hiệu từ A đến sớm hơn tín hiệu từ B là 0,0005 s. Từ thông tin trên, ta có thể xác định được tàu thuỷ thuộc đường hypebol nào? Viết phương trình chính tắc của hypebol đó theo đơn vị kilômét.

Phương pháp giải:

Gắn hệ trục tọa độ, sau đó tìm phương trình hyperbol đi qua vị trí tàu thủy

Lời giải:

Gọi M là vị trí tàu thu tín hiệu. Gọi $t_A,t_B$ lần lượt là thời gian tín hiệu truyền từ trạm phát A,B đến M. Theo đề bài, ta có $t_A-t_B=-0,0005s$.

Suy ra $MA-MB=v.t_A-v.t_B=292000.\left(-0,0005\right)=-146km$.

Gọi (H) là hyperbol ở dạng chính tắc nhận A,B làm hai tiêu điểm và đi qua M. Khi đó ta có:

$\{\begin{array}{l}2a=\left|MA-MB\right|=146\\ 2c=AB=300\end{array}\Rightarrow \{\begin{array}{l}a=73\\ c=150\end{array}\Rightarrow \{\begin{array}{l}a=73\\ b^2=c^2-a^2=17171\end{array}$

Vậy phương trình chính tắc của (H) là: $\frac{x^2}{5329}-\frac{y^2}{17171}=1$.

Bài 7.25 trang 56 SGK Toán 10 Tập 2: Khúc của của một con đường có dạng hình parabol, điềm đầu vào khúc cua là A, điểm cuối là B, khoảng cách AB = 400 m. Đỉnh parabol (P) của khúc của cách đường thẳng ABmột khoảng 20 m và cách đều A, B (H.7.34).

a) Lập phương trình chính tắc của (P), với 1 đơn vị đo trong mặt phẳng toạ độ tương ứng 1 m trên thực tế.

b) Lập phương trình chính tắc của (P), với 1 đơn vị đo trong mặt phẳng toạ độ tương ứng 1 km trên thực tế.

Phương pháp giải:

Gọi phương trình chính tắc  của (P)  và sử dụng  điều kiện (P) đi qua  điểm thỏa mãn để tìm phương trình (P).

Lời giải:

Phương trình chính tắc của parabol (P) có dạng $y^2=2px\left(p>0\right)$.

a) Khi 1 đơn vị đo trong mặt phẳng  tọa độ ứng với  1m trên thực tế, ta có $B\left(20;200\right)$.

Thay tọa độ điểm B vào phương trình của (P) ta được ${200}^2=2p.20\iff p=1000$.

Vậy phương trình chính tắc của (P) là: $y^2=2000x$.

b) Khi 1 đơn vị đo trong mặt phẳng tọa độ ứng với 1km trên thực tế, ta có  $B\left(0,02;0,2\right)$.

Tương tự, ta có phương trình chính tắc của (P) là $y^2=2x$.