Lời giải bài tập SBT Toán 10 Bài tập cuối chương VII sách Kết nối tri thức ngắn gọn, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi trong SBT Toán 10 Bài tập cuối chương VII từ đó học tốt môn Toán 10.

SBT Toán 10 Kết nối tri thức: Bài tập cuối chương VII

Câu hỏi trang 47 SBT Toán 10

Bài 7.38 trang 47 SBT Toán 10 Tập 2: Trong các phương trình sau, phương trình nào là phương trình chính tắc của đường hypebol?

A. 16x² – 5y² = –80;

B. x² = 4y;

C. $\frac{x^2}{4}-\frac{y^2}{1}=1$;

D. $\frac{x^2}{4}+\frac{y^2}{1}=1$.

Lời giải:

Đáp án đúng là: C

Phương trình chính tắc của đường hypebol có dạng $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$. (trong đó a, b > 0)

Do đó, $\frac{x^2}{4}-\frac{y^2}{1}=1$là một phương trình chính tắc của đường hypebol.

Bài 7.39 trang 47 SBT Toán 10 Tập 2: Cho hai điểm A(–1; 0) và B(–2; 3). Phương trình đường thẳng đi qua B và vuông góc với AB là

A. x – 3y + 11 = 0;

B. x – 3y + 1 = 0;

C. –x – 3y + 7 = 0;

D. 3x + y + 3 = 0.

Lời giải:

Đáp án đúng là: A

Đường thẳng đi qua B và vuông góc với AB nhận vectơ $\overrightarrow{AB}=\left(-1;3\right)$ là vectơ pháp tuyến.

Phương trình đường thẳng đi qua B và vuông góc với AB là:

–1(x + 2) + 3(y – 3) = 0

⇔ –x + 3y – 2 – 9 = 0

⇔ x – 3y + 11 = 0.

Bài 7.40 trang 47 SBT Toán 10 Tập 2: Cho điểm A(2; 3) và đường thẳng d: x + y + 3 = 0. Khoảng cách từ điểm A đến đường thẳng d là

A. $\frac{6}{\sqrt{13}}$;

B. $4\sqrt{2}$;

C. 8;

D. $2\sqrt{2}$.

Lời giải:

Đáp án đúng là: B

Khoảng cách từ điểm A đến đường thẳng d là:

Bài 7.41 trang 47 SBT Toán 10 Tập 2: Cho hai đường thẳng d: x – 2y – 5 = 0 và k: x + 3y + 3 = 0. Góc giữa hai đường thẳng d và k là

A. 30°;

B. 135°;

C. 45°;

D. 60°.

Lời giải:

Đáp án đúng là: C

Xét d: x – 2y – 5 = 0 và k: x + 3y + 3 = 0 có các vectơ pháp tuyến lần lượt là:

$\overrightarrow{n_d}=\left(1;-2\right)$

$\overrightarrow{n_k}=\left(1;3\right)$

Gọi φ là góc giữa hai đường thẳng d và k.

Ta có: 

Vậy góc giữa hai đường thẳng là φ = 45°.

Câu hỏi trang 48 SBT Toán 10

Bài 7.42 trang 48 SBT Toán 10 Tập 2: Cho đường tròn (C) có phương trình (x – 2)² + (y + 3)² = 9. Tâm I và bán kính R của đường tròn (C) là

A. I(2; –3), R = 9;

B. I(–2; 3), R = 3;

C. I(–2; 3), R = 9;

D. I(2; –3), R = 3.

Lời giải:

Đáp án đúng là: D

Xét phương trình đường tròn: (x – 2)² + (y + 3)² = 9 ta có:

Tâm I(2; –3)

Bán kính: R = $\sqrt{9}$ = 3.

Bài 7.43 trang 48 SBT Toán 10 Tập 2: Cho elip (E) có phương trình $\frac{x^2}{16}+\frac{y^2}{7}=1$. Điểm nào sau đây là một tiêu điểm của (E)?

A. (0; 3);

B. (4; 0);

C. (3; 0);

D. (0; 4).

Lời giải:

Đáp án đúng là: C

Xét phương trình elip: $\frac{x^2}{16}+\frac{y^2}{7}=1$ ta có:

a² = 16

b² = 7

$c=\sqrt{a^2-b^2}=\sqrt{16-7}=3$

Do đó, elip có hai tiêu điểm là: F₁(3; 0) và F₂(–3; 0).

Bài 7.44 trang 48 SBT Toán 10 Tập 2: Đường thẳng qua A(1; –1) và B(–2; –4) có phương trình là

A. 

B. 

C. 

D. 

Lời giải:

Đáp án đúng là: D

Đường thẳng qua A(1; –1) và B(–2; –4) có một vectơ chỉ phương là: $\overrightarrow{AB}=\left(-3;-3\right)$ hay có một vectơ chỉ phương khác là: $\overrightarrow{u}=\left(1;1\right)$.

Chọn điểm (–2; –4) thuộc đường thẳng AB. Phương trình tham số của đường thẳng AB là:

Bài 7.45 trang 48 SBT Toán 10 Tập 2: Cho hypebol (H) có phương trình chính tắc $\frac{x^2}{36}-\frac{y^2}{13}=1$.Tiêu cự của hypebol là

A. 7;

B. 14;

C. $2\sqrt{23}$;

D. $\sqrt{23}$.

Lời giải:

Đáp án đúng là: B

Xét phương trình chính tắc $\frac{x^2}{36}-\frac{y^2}{13}=1$ có:

a² = 36

b² = 13

$c=\sqrt{a^2+b^2}=\sqrt{36+13}=\sqrt{49}=7$

Do đó, tiêu cự là: 2c = 2 . 7 = 14.

Bài 7.46 trang 48 SBT Toán 10 Tập 2: Cho hai điểm A(0; – 2), B(2; 4). Phương trình đường tròn tâm A đi qua điểm B là

A. x² + (y + 2)² = 40;

B. x² + (y + 2)² = 10;

C. x² + (y – 2)² = 40;

D. x² + (y – 2)² = 10.

Lời giải:

Đáp án đúng là: A

Ta có: AB = $\sqrt{{(2-0)}^2+{(4+2)}^2}=2\sqrt{10}$

Đường tròn tâm A đi qua điểm B có bán kính R = AB = $2\sqrt{10}$

Phương trình đường tròn tâm A đi qua điểm B là:

(x – 0)² + (y + 2)² = ($2\sqrt{10}$)²

⇔ x² + (y + 2)² = 40.

Bài 7.47 trang 48 SBT Toán 10 Tập 2: Phương trình chính tắc của parabol (P) đi qua điểm E(2; 2) là

A. x² = 2y;

B. x² = 4y;

C. x² = y;

D. y = 2x².

Lời giải:

Đáp án đúng là: A

Thay tọa độ điểm E(2; 2) vào phương trình x² = 2y , ta có:

2² = 2.2

Do đó, phương trình chính tắc của parabol (P) đi qua điểm E(2; 2) là x² = 2y.

Bài 7.48 trang 48 SBT Toán 10 Tập 2: Cho đường tròn (C) có phương trình (x + 1)² + (y + 1)² = 4 và điểm M(1; –1) thuộc đường tròn. Phương trình tiếp tuyến của đường tròn tại điểm M là

A. y + 1 = 0;

B. y = 0;

C. x + 1 = 0;

D. x – 1 = 0.

Lời giải:

Đáp án đúng là: D

Đường tròn (C) có tâm I(–1; –1) và bán kính R = 2.

Tiếp tuyến của đường tròn tại M nhận vectơ $\overrightarrow{IM}=\left(2;0\right)$ làm vectơ pháp tuyến

Phương trình tiếp tuyến của đường tròn tại điểm M là:

2(x – 1) + 0.(y + 1) = 0

⇔ 2x – 2 = 0

⇔ x – 1 = 0.

Câu hỏi trang 49 SBT Toán 10

Bài 7.49 trang 49 SBT Toán 10 Tập 2: Cho đường thẳng d: 4x + 3y – 2 = 0 và đường thẳng . Vị trí tương đối của hai đường thẳng d và k là

A. trùng nhau;

B. song song;

C. cắt nhau nhưng không vuông góc;

D. vuông góc.

Lời giải:

Đáp án đúng là: A

Đường thẳng d: 4x + 3y – 2 = 0 và đường thẳng 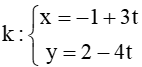 có vectơ pháp tuyến và vectơ chỉ phương lần lượt là: $\overrightarrow{n_d}=\left(4;3\right)$, $\overrightarrow{u_k}=\left(3;-4\right)$

Do đó, đường thẳng k có vectơ pháp tuyến là: $\overrightarrow{n_k}=\left(4;3\right)$.

Do đó, $\overrightarrow{n_d}=\overrightarrow{n_k}$ nên d và k hoặc song song hoặc trùng nhau.

Xét điểm $\left(1;-\frac{2}{3}\right)$ thuộc đường thẳng d.

Thay x = 1, y = $-\frac{2}{3}$ vào phương trình tham số của đường thẳng k ta có:

Do đó, $\left(1;-\frac{2}{3}\right)$ cũng thuộc vào đường thẳng k

Vậy d và k trùng nhau.

Bài 7.50 trang 49 SBT Toán 10 Tập 2: Phương trình chính tắc của elip (E) đi qua điểm M(8; 0) và có tiêu cự bằng 6 là

A. $\frac{x^2}{64}+\frac{y^2}{100}=1$;

B. $\frac{x^2}{64}+\frac{y^2}{28}=1$;

C. $\frac{x^2}{64}+\frac{y^2}{73}=1$;

D. $\frac{x^2}{64}+\frac{y^2}{55}=1$.

Lời giải:

Đáp án đúng là: D

Gọi phương trình chính tắc của elip (E) là: $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ với a > b > 0

Elip (E) đi qua điểm M(8; 0) nên ta có:

$\frac{8^2}{a^2}+\frac{0^2}{b^2}=1$ ⇔ a² = 8² = 64

Mà tiêu cự là 2c = 6 ⇔ c = 3

Ta có:

Vậy phương trình chính tắc của elip (E) là: $\frac{x^2}{64}+\frac{y^2}{55}=1$.

Bài 7.51 trang 49 SBT Toán 10 Tập 2: Cho điểm I(1; – 1) và đường thẳng d: x – y + 2 = 0. Phương trình đường tròn tâm I tiếp xúc với đường thẳng d là

A. (x – 1)² + (y + 1)² = 4;

B. (x + 1)² + (y – 1)² = 4;

C. (x – 1)² + (y + 1)² = 8;

D. (x + 1)² + (y – 1)² = 8.

Lời giải:

Đáp án đúng là: C

Đường tròn tâm I tiếp xúc với đường thẳng d nên ta có bán kính

R = d(I, d) = 

Phương trình đường tròn tâm I tiếp xúc với đường thẳng d là:

(x – 1)² + (y + 1)² = ($2\sqrt{2}$)²

⇔ (x – 1)² + (y + 1)² = 8

Bài 7.52 trang 49 SBT Toán 10 Tập 2: Cho đường thẳng d: x – y + 3 = 0. Phương trình đường thẳng song song với d và cách d một khoảng là $\sqrt{2}$ là

A. x + y + 1 = 0 và x + y + 3 = 0;

B. x – y – 1 = 0;

C. x – y + 3 = 0;

D. x – y + 3 = 0 và x – y – 1 = 0.

Lời giải:

Đáp án đúng là: (không có đáp án phù hợp)

Phương trình đường thẳng song song với d có dạng là: d’: x – y + c = 0 với c ≠ 3

Chọn điểm A(1; 4) thuộc đường thẳng d

Do d’ // d và d’ cách d một khoảng là $\sqrt{2}$ nên ta có:

d(A, d’) = $\sqrt{2}$

⇔ |c – 3| = 2 (*)

TH1: c – 3 ≥ 0 hay c ≥ 3

(*) ⇔ c – 3 = 2 ⇔ c = 5 (thỏa mãn)

TH2: c – 3 < 0 hay c < 3

(*) ⇔ –c + 3 = 2 ⇔ c = 1 (thỏa mãn)

Với c = 5 ta có, d’: x – y + 5 = 0.

Với c = 1 ta có, d’: x – y + 1 = 0.

Bài 7.53 trang 49 SBT Toán 10 Tập 2: Trong mặt phẳng Oxy, cho điểm M(–3; 2) và vectơ $\overrightarrow{u}=\left(2;-5\right)$. Viết phương trình tham số của đường thẳng d đi qua M và nhận $\overrightarrow{u}$ là một vectơ chỉ phương.

Lời giải:

Phương trình tham số của đường thẳng d đi qua M(–3; 2)và nhận $\overrightarrow{u}=\left(2;-5\right)$ là một vectơ chỉ phương là

Bài 7.54 trang 49 SBT Toán 10 Tập 2: Trong mặt phẳng Oxy, cho điểm N(2; –1) và vectơ $\overrightarrow{n}=\left(3;-1\right)$.Viết phương trình tổng quát của đường thẳng d đi qua N và nhận $\overrightarrow{n}$ là một vectơ pháp tuyến.

Lời giải:

Phương trình tổng quát của đường thẳng d đi qua N và nhận $\overrightarrow{n}$ là một vectơ pháp tuyến là:

3(x – 2) – 1(y + 1) = 0

⇔ 3x – y – 6 – 1 = 0

⇔ 3x – y – 7 = 0.

Bài 7.55 trang 49 SBT Toán 10 Tập 2: Cho tam giác ABC với A(1; –1), B(3; 5), C(–2; 4).

a) Viết phương trình tham số của đường thẳng AB.

b) Viết phương trình đường cao AH của tam giác ABC.

c) Tính khoảng cách từ điểm A đến đường thẳng BC.

d) Tính sin của góc giữa hai đường thẳng AB và AC.

Lời giải:

a)

Ta có $\overrightarrow{AB}=\left(2;6\right)$ là một vectơ chỉ phương của đường thẳng AB nên vectơ $\overrightarrow{u}=\left(1;3\right)$ cũng là một vectơ chỉ phương của AB.

Đường thẳng AB đi qua điểm A(1; –1) và nhận $\overrightarrow{u}=\left(1;3\right)$ là một vectơ chỉ phương có phương trình tham số là 

b)

Do AH vuông góc với BC nên $\overrightarrow{BC}=\left(-5;-1\right)$ là một vectơ pháp tuyến của đường cao AH.

Đường cao AH đi qua điểm A(1; –1) nhận $\overrightarrow{n}=-\overrightarrow{BC}=\left(5;1\right)$ là một vectơ pháp tuyến có phương trình tổng quát là:

5(x – 1) + 1(y + 1) = 0

⇔ 5x – 5 + y + 1 = 0

⇔ 5x + y – 4 = 0.

c)

Đường thẳng BC nhận vectơ $\overrightarrow{BC}=\left(-5;-1\right)$ là một vectơ chỉ phương nên BC nhận $\overrightarrow{n\text{'}}=\left(1;-5\right)$ là một vectơ pháp tuyến.

Do đó phương trình đường thẳng BC là:

1(x – 3) – 5(y – 5) = 0

⇔ x – 3 – 5y + 25 = 0

⇔ x – 5y + 22 = 0.

Khoảng cách từ điểm A(1; –1) đến đường thẳng BC là

d)

Gọi α là góc giữa hai đường thẳng AB và AC có hai vectơ chỉ phương lần lượt là: $\overrightarrow{AB}=\left(2;6\right),\overrightarrow{AC}=\left(-3;5\right)$

Khi đó

Do α là góc giữa hai đường thẳng nên sinα > 0.

Lại có sin²α + cos²α = 1.

$\Rightarrow \sin \alpha =\sqrt{1-{\cos }^2\alpha }=\frac{7}{\sqrt{85}}$

Câu hỏi trang 50 SBT Toán 10

Bài 7.56 trang 50 SBT Toán 10 Tập 2: Trong mặt phẳng Oxy, cho hai điểm A(–1; 0) và B(3; 1).

a) Viết phương trình đường tròn tâm A và đi qua B.

b) Viết phương trình tổng quát của đường thẳng AB.

c) Viết phương trình đường tròn tâm O và tiếp xúc với đường thẳng AB.

Lời giải:

a)

Đường tròn tâm A đi qua B có bán kính R = AB = $\sqrt{{(3+1)}^2+{(1-0)}^2}=\sqrt{17}$.

Vậy phương trình đường tròn tâm A đi qua B là:

(x + 1)² + (y – 0)² = ($\sqrt{17}$)²

⇔ (x + 1)² + y² = 17.

b)

Ta có $\overrightarrow{AB}=\left(4;1\right)$ là một vectơ chỉ phương của đường thẳng AB. Do đó $\overrightarrow{n}=\left(-1;4\right)$ là một vectơ pháp tuyến của AB.

Phương trình đường thẳng AB là:

–1(x + 1) + 4(y – 0) = 0

⇔ –x – 1 + 4y = 0

⇔ x – 4y + 1 = 0.

c)

Đường tròn tâm O và tiếp xúc với đường thẳng AB có bán kính là

Vậy phương trình đường tròn tâm O tiếp xúc với AB là

${(x-0)}^2+{(y-0)}^2={\left(\frac{1}{\sqrt{17}}\right)}^2\iff x^2+y^2=\frac{1}{17}$.

Bài 7.57 trang 50 SBT Toán 10 Tập 2: Cho đường tròn (C) có phương trình x² + y² – 4x + 6y – 12 = 0.

a) Tìm toạ độ tâm I và bán kính R của (C).

b) Chứng minh rằng điểm M(5; 1) thuộc (C). Viết phương trình tiếp tuyến d của (C) tại M.

Lời giải:

a)

Xét phương trình đường tròn (C) , ta có:

I (a; b) với a = – 4 : (–2) = 2, b = 6 : (–2) = –3, do đó, I (2; –3)

$R=\sqrt{2^2+{(-3)}^2-(-12)}=5$.

b)

Thay toạ độ điểm M vào phương trình của đường tròn (C) ta có

5² + 1² – 4.5 + 6.1 – 12 = 0 (luôn đúng)

nên điểm M thuộc đường tròn (C).

Tiếp tuyến d của (C) tại điểm M là đường thẳng đi qua M và vuông góc với IM nên có một vectơ pháp tuyến là $\overrightarrow{IM}=\left(3;4\right)$.

Vậy phương trình của tiếp tuyến d là:

3(x – 5) + 4(y – 1) = 0

⇔ 3x + 4y – 19 = 0.

Bài 7.58 trang 50 SBT Toán 10 Tập 2: Các phương trình dưới đây là phương trình chính tắc của đường nào? Khi đó hãy tìm các tiêu điểm, tiêu cự, đường chuẩn (nếu là đường parabol).

a) y²= 10x.

b) x² – y² = 1.

c) $\frac{x^2}{25}+\frac{y^2}{16}=1$.

Lời giải:

a)

y² = 10x là phương trình chính tắc của parabol.

Ta có y² = 10x = 2px ⇒ p = 5 $\Rightarrow \frac{p}{2}=\frac{5}{2}$.

Parabol trên có tiêu điểm là $F\left(\frac{5}{2};0\right)$, phương trình đường chuẩn là $x+\frac{5}{2}=0$.

b)

x² – y² = 1 là phương trình chính tắc của hypebol với a = b = 1 nên $c=\sqrt{a^2+b^2}=\sqrt{2}$

Tiêu điểm là $F_1\left(-\sqrt{2};0\right),F_2\left(\sqrt{2};0\right)$ tiêu cự là $2c=2\sqrt{2}$.

c)

$\frac{x^2}{25}+\frac{y^2}{16}=1$ là phương trình chính tắc của elip với a² = 25, b² = 16, $c=\sqrt{a^2-b^2}=3$

Tiêu điểm là F₁(–3; 0), F₂(3; 0), tiêu cự F₁F₂ = 2c = 2.3 = 6.

Bài 7.59 trang 50 SBT Toán 10 Tập 2: Cho elip (E) có phương trình là $\frac{x^2}{25}+\frac{y^2}{9}=1$. Tìm toạ độ các điểm M thuộc (E), biết rằng M nhìn hai tiêu điểm của (E) dưới một góc vuông.

Lời giải:

Elip $\frac{x^2}{25}+\frac{y^2}{9}=1$ có a² = 25, b² = 9, c = $\sqrt{a^2-b^2}=\sqrt{25-9}=4$ nên hai tiêu điểm là F₁(–4; 0), F₂(4; 0).

Do M nhìn hai tiêu điểm dưới một góc vuông nên M nằm trên đường tròn (C) tâm O đường kính F₁F₂ = 2.4 = 8 nên bán kính là R = 4.

Phương trình đường tròn (C) là:

x² + y² = 4² hay x² + y² = 16.

Khi đó toạ độ của M là nghiệm của hệ phương trình

Vậy ta tìm được bốn điểm M thoả mãn là $M\left(\pm \frac{5\sqrt{7}}{4};\pm \frac{9}{4}\right)$.

Bài 7.60 trang 50 SBT Toán 10 Tập 2: Lập phương trình chính tắc của parabol (P) biết rằng, (P) đi qua điểm A(2; 4). Khi đó hãy tìm điểm M thuộc (P) và cách tiêu điểm của (P) một khoảng bằng 5.

Lời giải:

Phương trình chính tắc của (P) có dạng y² = 2px.

Do (P) đi qua điểm A(2; 4) nên ta có: 4² = 2p.2 ⇔ p = 4 .

Vậy phương trình chính tắc của (P) là: y² = 8x với tiêu điểm F(2; 0).

Ta còn viết phương trình (P) dưới dạng: $x=\frac{y^2}{8}$.

Ta có:

Do điểm M thuộc (P) nên toạ độ của điểm M có dạng $M\left(\frac{t^2}{8};t\right)$

Từ giả thiết MF = 5 ta suy ra:

MF² = 25

$\iff {\left(\frac{t^2}{8}-2\right)}^2+t^2=25\iff \frac{t^2}{64}-\frac{t^2}{2}+4+t^2=25\iff \frac{t^2}{64}+\frac{t^2}{2}-21=0(*)$

Đặt t² = X (X ≥ 0) ta có:

(*) ⇔ $\frac{X^2}{64}+\frac{X}{2}-21=0$

Với X = 24 ⇔$t=\pm 2\sqrt{6}$

Vậy có hai điểm M thoả mãn là $M\left(3;\pm 2\sqrt{6}\right)$.

Bài 7.61 trang 50 SBT Toán 10 Tập 2: Hình vẽ bên minh hoạ một phòng thì thầm (whispering gallery) với mặt cắt ngang là một hình bán elip với chiều cao 24 feet và chiều rộng 80 feet. Một âm thanh được phát ra từ một tiêu điểm của phòng thì thầm có thể được nghe thấy tại tiêu điểm còn lại. Hỏi hai người nói thầm qua lại với nhau thì sẽ cách trung tâm của phòng bao nhiêu mét ? Theo đơn vị đo lường quốc tế, 1 feet = 0,3048 m.

Lời giải:

Theo đề bài, mặt cắt ngang là một hình bán elip với chiều cao 24 feet và chiều rộng 80 feet nên mặt cắt của phòng thì thầm là một nửa elip có a = 40 feet, b = 24 feet nên $c=\sqrt{a^2-b^2}=\sqrt{{40}^2-{24}^2}=32$ feet

Vậy nếu hai người nói chuyện với nhau trong phòng thì sẽ cách trung tâm phòng một nửa tiêu cự là c = 32 feet = 32 . 0,3048 m = 9,7536 m.