Toptailieu.vn xin giới thiệu 06 câu trắc nghiệm Bài tập cuối chương 7 Kết nối tri thức (có đáp án 2023) CHỌN LỌC, hay nhất giúp học sinh lớp 10 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.

Mời các bạn đón xem:

06 câu trắc nghiệm Bài tập cuối chương 7 Kết nối tri thức (có đáp án 2023) CHỌN LỌC

Lý thuyết

I. Phương trình đường thẳng

1. Vectơ chỉ phương của đường thẳng

Định nghĩa : 

vectơ  được gọi là vectơ chỉ phương của đường thẳng Δ nếu ≠  và giá của  song song hoặc trùng với Δ

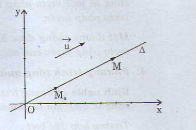
Nhận xét :

- Nếu  là một vectơ chỉ phương của đường thẳng Δ thì k (k ≠ 0) cũng là một vectơ chỉ phương của Δ , do đó một đường thẳng có vô số vectơ chỉ phương.

- Một đường thẳng hoàn toàn được xác định nếu biết một điểm và một vectơ chỉ phương của đường thẳng đó.

2. Phương trình tham số của đường thẳng

- Phương trình tham số của đường thẳng Δ đi qua điểm M_o(x_o;y_o) và nhận vectơ (u₁;u₂) làm vectơ chỉ phương là: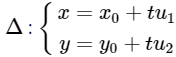 

-Khi u₁ ≠ 0 thì tỉ số k = 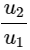 được gọi là hệ số góc của đường thẳng.

Từ đây, ta có phương trình đường thẳng Δ đi qua điểm M_o(x_o;y_o) và có hệ số góc k là:

y - y_o = k(x - x_o)

Chú ý: Ta đã biết hệ số góc k = tanα với góc α là góc của đường thẳng Δ hợp với chiều dương của trục Ox

3. Vectơ pháp tuyến của đường thẳng 

Định nghĩa: Vectơ  được gọi là vectơ pháp tuyến của đường thẳng Δ nếu   ≠ và  vuông góc với vectơ chỉ phương của Δ

Nhận xét:

- Nếu   là một vectơ pháp tuyến của đường thẳng Δ thì k (k ≠ 0) cũng là một vectơ pháp tuyến của Δ, do đó một đường thẳng có vô số vec tơ pháp tuyến.

- Một đường thẳng được hoàn toàn xác định nếu biết một và một vectơ pháp tuyến của nó.

4. Phương trình tổng quát của đường thẳng

Định nghĩa: Phương trình ax + by + c = 0 với a và b không đồng thời bằng 0, được gọi là phương trình tổng quát của đường thẳng.

Trường hợp đặc biết:

+  Nếu a = 0 ⇒ y = ; Δ // Ox hoặc trùng Ox (khi c=0)

+ Nếu b = 0 ⇒ x = ; Δ // Oy hoặc trùng Oy (khi c=0)

+ Nếu c = 0 ⇒ ax + by = 0 ⇒ Δ đi qua gốc tọa độ

+ Nếu Δ cắt Ox tại A(a;0) và Oy tại B(0;b) thì ta có phương trình đoạn chắn của đường thẳng Δ :

5. Vị trí tương đối của hai đường thẳng

Xét hai đường thẳng ∆₁ và ∆₂ 

có phương trình tổng quát lần lượt là :

a₁x+b₁y + c₁ = 0 và a₂x+b₂y +c₂ = 0

Điểm M_o(x_o;y_o) là điểm chung của  ∆₁ và ∆₂  khi và chỉ khi (x_o;y_o) là nghiệm của hệ hai phương trình:

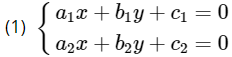
Ta có các trường hợp sau:

a) Hệ (1) có một nghiệm: ∆₁ cắt ∆₂

b) Hệ (1) vô nghiệm: ∆₁ // ∆₂

c) Hệ (1) có vô số nghiệm: ∆₁ ≡ ∆₂

6. Góc giữa hai đường thẳng

Hai đường thẳng ∆₁ và ∆₂ cắt nhau tạo thành 4 góc.

Nếu ∆₁ không vuông góc với ∆₂ thì góc nhọn trong số bốn góc đó được gọi là góc giữa hai đường thẳng ∆₁ và ∆₂.

Nếu ∆₁ vuông góc với  ∆₂ thì ta nói góc giữa ∆₁ và ∆₂ bằng 90⁰.

Trường hợp ∆₁ và ∆₂ song song hoặc trùng nhau thì ta quy ước góc giữa  ∆₁ và ∆₂ bằng 0⁰.

Như vậy góc giữa hai đường thẳng luôn bé hơn hoặc bằng 90⁰  

Góc giữa hai đường thẳng ∆₁ và ∆₂ được kí hiệu là 

Cho hai đường thẳng:

∆₁: a₁x+b₁y + c₁ = 0 

∆₂: a₂x+b₂y + c₂ = 0

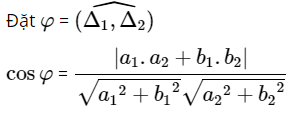
Chú ý:

+ Δ₁ ⊥ Δ₂ ⇔ n₁ ⊥ n₂ ⇔ a₁.a₂ + b₁.b₂ = 0

+ Nếu Δ₁ và Δ₂ có phương trình y = k₁ x + m₁ và y = k₂ x + m₂ thì  

Δ₁ ⊥ Δ₂ ⇔ k₁.k₂ = -1

7. Công thức tính khoảng cách từ một điểm đến một đường thẳng

Trong mặt phẳng Oxy cho đường thẳng Δ có phương trình ax + by + c = 0 và điểm M_o(x_o;y_o)).

Khoảng cách từ điểm M_o đến đường thẳng Δ kí hiệu là d(M_o;Δ), được tính bởi công thức

II. Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách

1. Các kiến thức cần nhớ

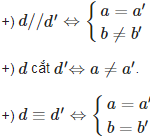
2. Các dạng toán thường gặp

Dạng 1: Chỉ ra vị trí tương đối của hai đường thẳng cho trước. Tìm tham số m để các đường thẳng thỏa mãn vị trí tương đối cho trước.

Phương pháp:

Cho hai đường thẳng d:y = ax + b (a ≠ 0) và d':y = a'x + b' (a' ≠ 0).

.

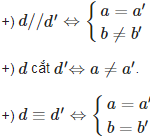Dạng 2:  Viết phương trình đường thẳng

Phương pháp:

+) Sử dụng vị trí tương đối của hai đường thẳng để xác định hệ số.

Ngoài ra ta còn sử dụng các kiến thức sau

+) Ta có y = ax + b với a ≠ 0, b ≠ 0 là phương trình đường thẳng cắt trục tung tại điểm A(0;b), cắt trục hoành tại điểm B(-;0).

+) Điểm M(x_o;y_o) thuộc đường thẳng y = ax + b khi và chỉ khi y_o = ax_o + b.

Dạng 3: Tìm điểm cố định mà đường thẳng d luôn đi qua với mọi tham số m

Phương pháp:

Gọi M(x;y) là điểm cần tìm khi đó tọa độ điểm M(x;y) thỏa mãn phương trình đường thẳng d.

Đưa phương trình đường thẳng d về phương trình bậc nhất ẩn m.

Từ đó để phương trình bậc nhất ax + b = 0 luôn đúng thì a =  = 0

Giải điều kiện ta tìm được x, y.

Khi đó M(x;y) là điểm cố định cần tìm.

III. Đường tròn trong mặt phẳng tọa độ

1. Phương trình đường tròn

Điểm M(x;y) thuộc đường tròn (C), tâm (a;b), bán kính R khi và chỉ khi

(x - a)² + (y - b)² = R² (1)

Ta gọi (1) là phương trình của đường tròn (C).

2. Phương trình tiếp tuyến của đường tròn

Cho điểm M(x_o;y_o) thuộc đường tròn (C):(x - a)² + (y - b)² = R² (tâm I(a;b), bán kính R). Khi đó, tiếp tuyến Δ của (C) tại M(x_o;y_o) có vecto pháp tuyến  = (a - x_o; b - y_o) và phương trình 

(a - x_o) (x - x_o) + (b - y_o) (y - y_o) = 0

IV. Ba đường conic

1. Đường elip

1.1. Định nghĩa đường elip

Cho hai điểm F₁, F₂ cố định có khoảng cách F₁F₂ = 2c (c > 0)

Đường elip (còn gọi là elip) là tập hợp các điểm M trong mặt phẳng sao cho MF₁ + MF₂ = 2a, trong đó a là số cho trước lớn hơn c.

Hai điểm F₁ và F₂ được gọi là hai tiêu điểm của elip.

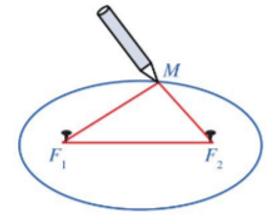
1.2. Phương trình chính tắc của elip

Trong mặt phẳng, xét đường elip (E) là tập hợp các điểm M sao cho MF₁ + MF₂ = 2a, ở đó F₁F₂ = 2c (với a > c > 0).

Ta chọn hệ trục tọa độ Oxy có gốc là trung điểm của F₁F₂, trục Oy là đường trung trực của F₁F₂ và F₂ nằm trên tia Ox (Hình 52). Khi đó, F₁(–c ; 0) và F₂(c ; 0) là hai tiêu điểm của elip (E).

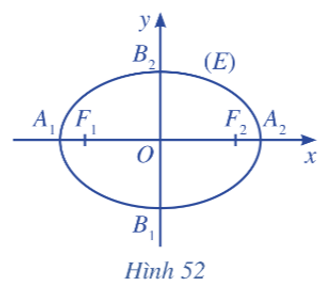
Khi chọn hệ trục tọa độ như trên, phương trình đường elip có thể viết dưới dạng , trong đó a > b > 0.

Đây gọi là phương trình chính tắc của elip.

Chú ý: Đối với elip (E) có phương trình chính tắc như đã nêu ở trên, ta có:

+ c² = a² – b², ở đó 2c = F₁F₂.

+ Nếu điểm M(x ; y) thuộc elip (E) thì –a ≤ x ≤ a.

2. Đường hypebol

2.1. Định nghĩa đường hypebol

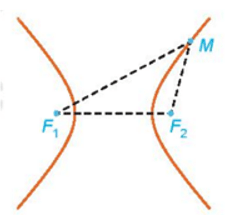
Cho hai điểm F₁ và F₂ cố định có khoảng cách F₁F₂ = 2c (c > 0).

Đường hypebol (còn gọi là hypebol) là tập hợp các điểm M sao cho |MF₁ – MF₂| = 2a, trong đó a là số nguyên dương cho trước nhỏ hơn c.

Hai điểm F₁ và F₂ được gọi là hai tiêu điểm của hypebol.

2.2. Phương trình chính tắc của đường hypebol

Chọn hệ trục tọa độ tương tự elip, ta chọn Ox là đường thẳng F₁F₂, trục Oy là đường trung trực của đoạn thẳng F₁F₂ = 2c (c > 0), gốc tọa độ O là trung điểm của đoạn thẳng F₁F₂ (Hình 54).

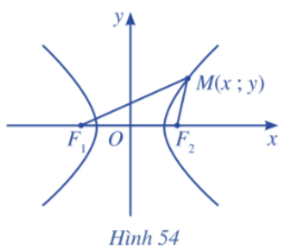
Khi chọn hệ trục tọa độ như trên, phương trình đường hypebol có thể viết dưới dạng , trong đó a > 0, b > 0.

Đây gọi là phương trình chính tắc của hypebol.

Chú ý: Đối với hypebol (H) có phương trình chính tắc như đã nêu ở trên, ta có:

+ c² = a² + b², ở đó 2c = F₁F₂ và điều kiện a > b là không bắt buộc.

+ Nếu điểm M(x ; y) thuộc hypebol (H) thì x ≤ –a hoặc x ≥ a.

3. Đường parabol

3.1. Định nghĩa đường parabol

Cho một điểm F cố định và một đường thẳng ∆ cố định không đi qua F.

Đường parabol (còn gọi là parabol) là tập hợp các điểm M trong mặt phẳng cách đều F và ∆.

Điểm F được gọi là tiêu điểm của parabol. Đường thẳng ∆ được gọi là đường chuẩn của parabol.

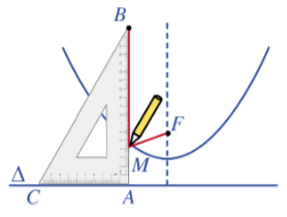
3.2. Phương trình chính tắc của parabol

Cho parabol (P) với tiêu điểm F và đường chuẩn ∆.

Kẻ FH vuông góc với ∆ (H ∈ ∆). Đặt FH = p > 0.

Ta chọn hệ trục tọa độ Oxy sao cho O là trung điểm của đoạn thẳng FH và F nằm trên tia Ox (Hình 56)

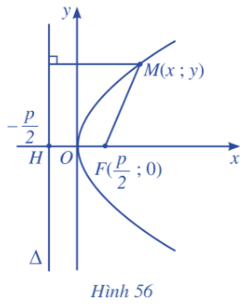
Khi chọn hệ trục tọa độ như trên, phương trình đường parabol có thể viết dưới dạng y² = 2px (p > 0).

Đây gọi là phương trình chính tắc của parabol.

Chú ý: Đối với parabol (P) có phương trình chính tắc y² = 2px (p > 0), ta có:

+ Tiêu điểm là F(;0) và phương trình đường chuẩn là: x +  = 0.

+ Nếu điểm M(x ; y) thuộc parabol (P) thì x ≥ 0.

Bài tập

Câu 1: Phương trình nào sau đây là phương trình tham số của đường thẳng?

A. 2x – y + 1 = 0.          

B.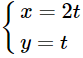 

C. x² + y² = 1.              

D. y = 2x + 3.

Lời giải:

Đáp án đúng là: B.

Phương trình tham số của đường thẳng có dạng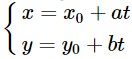 

Do đó trong các phương trình đã cho, thì phương trình ở đáp án B là phương trình tham số của đường thẳng với x₀ = y₀ = 0, a = 2 và b = 1.

Câu 2: Phương trình nào sau đây là phương trình tổng quát của đường thẳng?

A. – x – 2y  + 3 = 0. 

B.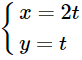   

C. y² = 2x. 

D. 

Lời giải:

Đáp án đúng là: A.

Phương trình tổng quát của đường thẳng có dạng ax + bx + c = 0 với a, b không đồng thời bằng 0. 

Do đó, trong các đáp án đã cho, phương trình ở đáp án A là phương trình tổng quát của đường thẳng với a = – 1, b = – 2, c = 3.

Câu 3: Phương trình nào sau đây là phương trình của đường tròn?

A. x²– y² = 1.                   

B. (x – 1)² + (y – 2)² = – 4.

C. x² + y² = 2.                 

D. y² = 8x.

Lời giải:

Đáp án đúng là: C.

Phương trình đường tròn có dạng: (x – a)² + (y – b)² = R². 

Trong các đáp án trên, phương trình ở đáp án C là phương trình đường tròn với a = 0, b = 0 và R =  . 

Chú ý: Phương trình ở đáp án B không phải là phương trình đường tròn vì – 4 < 0.

Câu 4: Phương trình nào sau đây là phương trình chính tắc của đường elip?

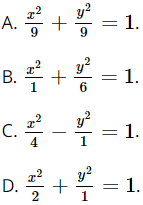
Lời giải:

Đáp án đúng là: D.

Phương trình chính tắc của đường elip có dạng   với a > b > 0. 

Ta có:  > >0. 

Do đó trong các đáp án đã cho, chỉ có phương trình ở đáp án D là phương trình chính tắc của đường elip.

Câu 5: Phương trình nào sau đây là phương trình chính tắc của đường hypebol?

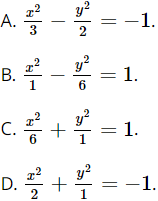
Lời giải:

Đáp án đúng là: B.

Phương trình chính tắc của đường hypebol có dạng   với a, b > 0. 

Do đó trong các đáp án đã cho, chỉ có phương trình ở đáp án B là phương trình chính tắc của đường hypebol.

Câu 6: Phương trình nào sau đây là phương trình chính tắc của đường parabol?

A. x² = 4y. 

B. x² = – 6y.

C. y² = 4x. 

D. y² = – 4x.

Lời giải:

Đáp án đúng là: C.

Phương trình chính tắc của đường parabol có dạng: y² = 2px (với p > 0). 

Do đó ta loại ngay đáp án A, B. 

Đáp án D có – 4 < 0 nên đây cũng không phải phương trình chính tắc của parabol. 

Vậy trong các đáp án đã cho, chỉ có phương trình ở đáp án C là phương trình chính tắc của parabol.

Xem thêm các bài giải Trắc nghiệm Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài 22: Ba đường conic

Bài 23: Quy tắc đếm

Bài 24: Hoán vị, chỉnh hợp và tổ hợp

Bài 25: Nhị thức

Bài tập cuối chương 8