Với giải Câu hỏi trang 35 Toán 10 Tập 2 Cánh Diều trong Bài 3: Các số liệu đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Toán 10 Cánh Diều trang 35 Bài 3: Các số liệu đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm
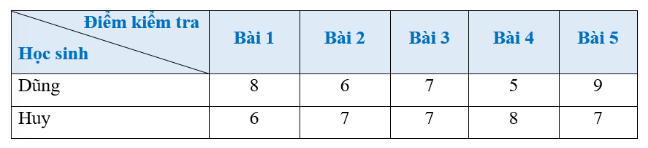
Kết quả làm bài kiểm tra môn Toán của bạn nào đồng đều hơn?
Lời giải:
Sau bài học này, ta giải quyết được bài toán trên như sau:
Số trung bình cộng điểm kiểm tra của bạn Dũng là:
Phương sai mẫu số liệu điểm kiểm tra của bạn Dũng là:
Số trung bình cộng điểm kiểm tra của bạn Huy là:
Phương sai mẫu số liệu điểm kiểm tra của bạn Huy là:
Vì 0,4 < 2 nên nên bạn Huy có kết quả kiểm tra môn Toán đồng đều hơn bạn Dũng.
1. Khoảng biến thiên. Khoảng tứ phân nhị
Hoạt động 1 trang 35 Toán lớp 10 Tập 2: Kết quả của 11 lần đo được thống kê trong mẫu số liệu sau:
2 5 16 8 7 9 10 12 14 11 6 (1)
a) Tìm hiệu giữa số đo lớn nhất và số đo nhỏ nhất.
b) Sắp xếp các số liệu của mẫu (1) theo thứ tự tăng dần. Tìm các giá trị Q1, Q2, Q3 là tứ phân vị của mẫu đó. Sau đó, tìm hiệu Q3 – Q1.
Lời giải:
a, Số đo lớn nhất là 16. số đo nhỏ nhất là 2
Hiệu giữa số đo lớn nhất và số đo nhỏ nhất là 16 - 2 = 14
b, Sắp xếp các số liệu của mẫu (1) theo thứ tự tăng dần ta đước:
2 5 6 7 8 9 10 11 12 14 16
Trung vị mẫu (1) là Q2 = 9
Trung vị của dãy 2 5 6 7 8 là Q1 = 6
Trung vị của dãy 10 11 12 14 16 là Q3 = 12
Vậy Q1 = 6, Q2 = 9, Q3 = 12
Do đó, hiệu Q3 - Q1 = 12 - 6 = 6
Xem thêm các lời giải SGK Toán 10 Cánh Diều hay, chi tiết khác:
Hoạt động 1 trang 35 Toán lớp 10 Tập 2: Kết quả của 11 lần đo được thống kê trong mẫu số liệu sau...
Hoạt động 3 trang 39 Toán lớp 10 Tập 2: Trong Ví dụ 2, phương sai của mẫu số liệu (4) là ![]() Tính
Tính ![]() ...
...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.