Với giải Câu hỏi trang 102 Toán 10 Tập 2 Cánh Diều trong Bài 6: Ba đường Conic giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Toán 10 Cánh Diều trang 102 Bài 6: Ba đường Conic
Bài 1 trang 102 Toán lớp 10 Tập 2: Phương trình nào sau đây là phương trình chính tắc của elip?
a) ;
b) ;
c) ;
d) .
Lời giải:
Phương trình chính tắc của elip có dạng , trong đó a > b > 0.
Do đó, ta loại ngay đáp án b).
Ở đáp án a, ta thấy a2 = b2 = 64, do đó không thỏa mãn điều kiện.
Ở đáp án d, ta thấy a2 = 25, b2 = 64, suy ra a = 5 và b = 8 nên a < b, không thỏa mãn.
Ở đáp án c, ta có a2 = 64, b2 = 25, suy ra a = 8, b = 5 nên a > b > 0, thỏa mãn.
Vậy trong các phương trình đã cho thì phương trình ở đáp án c) là phương trình chính tắc của elip.
Bài 2 trang 102 Toán lớp 10 Tập 2: Cho Elip (E) có phương trình chính tắc .Tìm tọa độ các giao điểm của (E) với trục Ox, Oy và tọa độ các tiêu điểm của (E).
Lời giải:
Ta có:
Do a > b > 0 nên elip (E) có a = 7, b = 5.
Ta có: c2 = a2 – b2 = 72 – 52 = 24, suy ra .
Vậy tọa độ các giao điểm của (E) với trục Ox là A1(– 7; 0), A2(7; 0), tọa độ các giao điểm của (E) với trục Oy là B1(0; – 5), B2(0; 5) và tọa độ các tiêu điểm của E là .
Bài 3 trang 102 Toán lớp 10 Tập 2: Viết phương trình chính tắc của elip (E), biết tọa độ hai giao điểm của (E) với Ox và Oy lần lượt là A1(– 5; 0) và B2(0; )
Lời giải:
Phương trình chính tắc của elip (E) có dạng , trong đó a > b > 0.
Elip (E) cắt trục Ox tại A1(– 5; 0), thay vào phương trình elip ta được:
, suy ra a = 5 (do a > 0).
Elip (E) cắt trục Oy tại , thay vào phương trình elip ta được: (do b > 0).
Vì 5 > nên a > b > 0 (thỏa mãn điều kiện).
Vậy phương trình chính tắc của elip (E) là .
Bài 4 trang 102 Toán lớp 10 Tập 2: Ta biết rằng Mặt Trăng chuyển động quanh Trái Đất theo quỹ đạo là một elip mà Trái Đất là một tiêu điểm. Elip đó có A1A2 = 768 800 km và B1B2 = 767 619 km (Nguồn: Ron Larson (2014), Precalculus Real Mathematics, Real People, Cengage) (Hình 62). Viết phương trình chính tắc của elip đó.
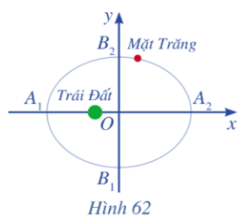
Lời giải:
Phương trình chính tắc của elip trên có dạng , trong đó a > b > 0.
Ta có Oy là đường trung trực của A1A2 nên O là trung điểm của A1A2 nên OA2 = .
Vì điểm A2 nằm trên trục Ox về phía bên phải điểm O và cách O một khoảng bằng 384 400 nên A2(384 800; 0).
Elip (E) cắt trục Ox tại A2(384 800; 0), thay vào phương trình elip ta được:
(do a > 0).
Lại có Ox là đường trung trực của B1B2 nên O là trung điểm của B1B2 nên OB2 = .
Vì điểm B2 nằm trên trục Oy về phía bên trên điểm O và cách O một khoảng bằng 338309,5 nên B2(0; 338309,5).
Elip (E) cắt trục Oy tại B2(0; 338309,5), thay vào phương trình elip ta được:
(do b > 0).
Vì 384 800 > 338309,5 nên a > b > 0 (thỏa mãn điều kiện).
Vậy phương trình chính tắc của elip (E) là .
a) ;
b) ;
c) ;
d) .
Lời giải:
Phương trình chính tắc của hypebol có dạng , trong đó a > 0, b > 0.
Do đó, ta loại ngay đáp án a.
Các phương trình ở các đáp án b, c, d đều là phương trình chính tắc của hypebol vì đều có dạng trên và thỏa mãn điều kiện a > 0, b > 0 với:
b) a = b = 3 > 0.
c) a = 3 > 0, b = 8 > 0.
d) a = 8 > 0, b = 3 > 0.
a) ;
b) .
Lời giải:
a) Ta có: .
Do đó hypebol trên có a = 3, b = 4 (do a > 0, b > 0).
Ta có: c2 = a2 + b2 = 32 + 42 = 25 = 52, suy ra c = 5.
Vậy tọa độ các tiêu điểm của hypebol trên là F1(– 5; 0) và F2(5; 0).
b) Ta có:
Suy ra a2 = 36, b2 = 25.
Ta có: c2 = a2 + b2 = 36 + 25 = 61, suy ra .
Vậy tọa độ các tiêu điểm của hypebol trên là F1(– ; 0) và F2(; 0).
Bài 7 trang 102 Toán lớp 10 Tập 2: Viết phương trình chính tắc của hypebol (H), biết N( ; 2) nằm trên (H) và hoành độ một giao điểm của (H) đối với trục Ox bằng 3.
Lời giải:
Phương trình chính tắc của hypebol (H) có dạng , trong đó a > 0, b > 0.
Hoành độ một giao điểm của (H) với trục Ox là 3, do đó tọa độ giao điểm của (H) với trục Ox là (3; 0). Thay tọa độ này vào phương trình hypebol, ta được:
(do a > 0).
Điểm nằm trên (H) nên tọa độ điểm N thỏa mãn phương trình (H), khi đó ta có: (do b > 0).
Vậy phương trình chính tắc của hypebol (H) là .
a) y2 = – 2x;
b) y2 = 2x;
c) x2 = – 2y;
d) .
Lời giải:
Phương trình chính tắc của parabol có dạng y2 = 2px (với p > 0).
a) Ta có: y2 = – 2x = 2 . (– 1)x, vì (– 1) < 0 nên đây không phải phương trình chính tắc của parabol.
b) Ta có: y2 = 2x = 2 . 1 . x, vì 1 > 0 nên đây là phương trình chính tắc của parabol với p = 1.
c) Phương trình x2 = – 2y không có dạng phương trình chính tắc của parabol nên đây không phải là phương trình chính tắc của parabol.
d) Ta có: , vì nên đây là phương trình chính tắc của parabol với .
Bài 9 trang 102 Toán lớp 10 Tập 2: Tìm tọa độ tiêu điểm và viết phương trình đường chuẩn của đường parabol trong mỗi trường hợp sau:
a) ;
b) .
Lời giải:
a) Ta có: .
Do đó parabol trên có p = (thỏa mãn p > 0).
Ta có: .
Vậy tọa độ tiêu điểm của parabol này là và phương trình đường chuẩn là .
b) Ta có: .
Do đó parabol trên có p = (thỏa mãn p > 0).
Ta có: .
Vậy tọa độ tiêu điểm của parabol này là và phương trình đường chuẩn là .
Lời giải:
Phương trình chính tắc của parabol có dạng y2 = 2px (với p > 0).
Tiêu điểm của parabol là F(6; 0).
Do đó, .
Vậy phương trình chính tắc của parabol là y2 = 2 . 12 x hay y2 = 24x.
Bài 11 trang 102 Toán lớp 10 Tập 2: Một chiếc đèn có mặt cắt ngang là hình parabol (Hình 63). Hình parabol có chiều rộng giữa hai mép vành là AB = 40 cm và chiều sâu h = 30 cm (h bằng khoảng cách từ O đến AB). Bóng đèn nằm ở tiêu điểm S. Viết phương trình chính tắc của parabol đó.
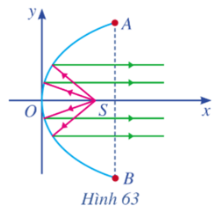
Lời giải:
Phương trình chính tắc của parabol có dạng y2 = 2px (với p > 0).
Vì AB = 40 và Ox là đường trung trực của đoạn AB nên khoảng cách từ điểm A đến trục Ox là .
Chiều sâu h bằng khoảng cách từ O đến AB và cũng chính bằng khoảng cách từ điểm A đến trục Oy và bằng 30.
Do đó, parabol đi qua điểm A có hoành độ là 30 (khoảng cách từ A đến trục Oy) và tung độ là 20 (khoảng cách từ A đến trục Ox) hay A(30; 20).
Thay tọa độ điểm A vào phương trình chính tắc của parabol, ta được:
202 = 2p . 30 ⇔ 60p = 400 ⇔ p = (thỏa mãn p > 0).
![]()
Xem thêm các bài giải bài tập Toán lớp 10 Cánh Diều hay, chi tiết khác:
Bài 1 trang 102 Toán lớp 10 Tập 2: Phương trình nào sau đây là phương trình chính tắc của elip?...
Bài 7 trang 102 Toán lớp 10 Tập 2: Viết phương trình chính tắc của hypebol (H), biết N( ; 2)...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.