SBT Toán 10 Kết nối tri thức trang 41: Bài tập cuối chương 3

Giang Ngày: 16-02-2023 Lớp 10

282

Với giải Câu hỏi trang 41 SBT Toán 10 Tập 1 Kết nối tri thức trong Bài tập cuối chương 3 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập SBT Toán 10. Mời các bạn đón xem:

SBT Toán 10 Kết nối tri thức trang 41: Bài tập cuối chương 3

Bài 3.24 trang 41 sách bài tập Toán lớp 10 Tập 1: Trên mặt phẳng tọa độ Oxy lấy điểm M thuộc nửa đường tròn đơn vị, sao cho $\hat{x O M} = 150 °$ (H.3.5).

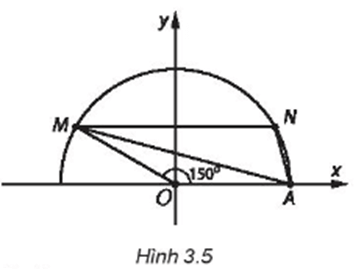
Bài 3.24 trang 41 sách bài tập Toán lớp 10 Tập 1

Lấy N đối xứng với M qua trục tung. Diện tích của tam giác MAN bằng

A. $\frac{\sqrt{3}}{4};$

B. $\frac{\sqrt{3}}{2};$

C. $\sqrt{3};$

D. $2 \sqrt{3} .$

Lời giải:

Đáp án đúng là: A

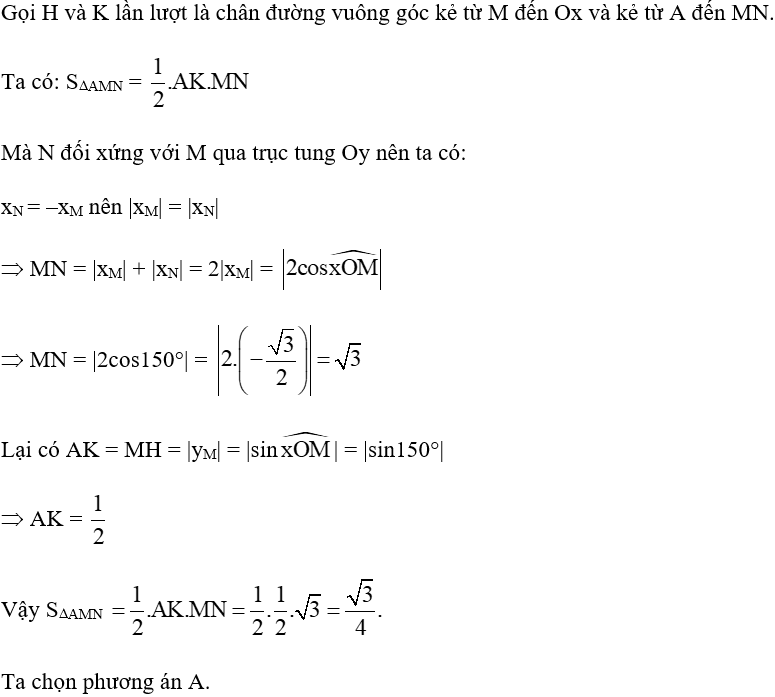
Bài 3.25 trang 42 sách bài tập Toán lớp 10 Tập 1: Cho cosα = $\frac{1}{4} .$ Giá trị của $P = \frac{\tan α + 2 \cot α}{2 \tan α + 3 \cot α}$ là

A. $- \frac{17}{33};$

B. $\frac{17}{33};$

C. $\frac{1}{2};$

D. $\frac{16}{33} .$

Lời giải:

Đáp án đúng là: B

Ta có cosα = $\frac{1}{4}$ $\Rightarrow$ cos²α = $\frac{1}{16}$

Mà sin²α + cos²α = 1

$\Rightarrow$ sin²α + $\frac{1}{16}$ = 1

$\Rightarrow$ sin²α = $\frac{15}{16}$

Ta có: $P = \frac{\tan α + 2 \cot α}{2 \tan α + 3 \cot α}$

$= \frac{\frac{\sin α}{c o s α} + \frac{2 c o s α}{\sin α}}{\frac{2 \sin α}{c o s α} + \frac{3 c o s α}{\sin α}}$ $= \frac{\frac{\sin^{2} α + 2 c o s^{2} α}{\sin α . c o s α}}{\frac{2 \sin^{2} α + 3 c o s^{2} α}{\sin α . c o s α}}$

$= \frac{\sin^{2} α + 2 c o s^{2} α}{2 \sin^{2} α + 3 c o s^{2} α}$ $= \frac{\frac{15}{16} + 2. \frac{1}{16}}{2. \frac{15}{16} + 3. \frac{1}{16}} = \frac{17}{33}$

Ta chọn phương án B.

Bài 3.26 trang 41 sách bài tập Toán lớp 10 Tập 1: Tam giác ABC có a = 2, b = 3, c = 4. Bán kính đường tròn ngoại tiếp của tam giác ABC là

A. $R = \frac{\sqrt{15}}{2};$

B. $R = \frac{7}{\sqrt{15}};$

C. $R = \frac{\sqrt{15}}{6};$

D. $R = \frac{8}{\sqrt{15}} .$

Lời giải:

Đáp án đúng là: D

Tam giác ABC có a = 2, b = 3, c = 4 nên:

$p = \frac{a + b + c}{2} = \frac{2 + 3 + 4}{2} = \frac{9}{2};$

• p – a = $\frac{5}{2};$

• p – b = $\frac{3}{2};$

• p – c = $\frac{1}{2};$

Áp dụng công thức Heron ta có:

$S = \sqrt{p . (p - a) (p - b) (p - c)}$

$\Rightarrow S = \sqrt{\frac{9}{2} . \frac{5}{2} . \frac{3}{2} . \frac{1}{2}} = \frac{3 \sqrt{15}}{4}$

Mà $S = \frac{a b c}{4 R} \Rightarrow R = \frac{a b c}{4 S} = \frac{2.3.4}{4. \frac{3 \sqrt{15}}{4}} = \frac{8}{\sqrt{15}} .$

Ta chọn phương án D.

Bài 3.27 trang 41 sách bài tập Toán lớp 10 Tập 1: Tam giác ABC có a = 4, b = 5, c = 6. Độ dài đường cao h_b bằng

A. $\frac{3 \sqrt{7}}{2};$

B. $\frac{3}{2 \sqrt{7}};$

C. $\frac{3 \sqrt{7}}{4};$

D. $\frac{3}{4 \sqrt{7}} .$

Lời giải:

Đáp án đúng là: A

Tam giác ABC có a = 4, b = 5, c = 6 nên:

• $p = \frac{a + b + c}{2} = \frac{4 + 5 + 6}{2} = \frac{15}{2};$

• p – a = $\frac{7}{2};$

• p – b = $\frac{5}{2};$

• p – c = $\frac{3}{2};$

Áp dụng công thức Heron ta có:

$S = \sqrt{p . (p - a) (p - b) (p - c)}$

$\Rightarrow S = \sqrt{\frac{15}{2} . \frac{7}{2} . \frac{5}{2} . \frac{3}{2}} = \frac{15 \sqrt{7}}{4}$

Mà $S = \frac{1}{2} h_{b} . b \Rightarrow h_{b} = \frac{2 S}{b} = \frac{2. \frac{15 \sqrt{7}}{4}}{5} = \frac{3 \sqrt{7}}{2} .$

Ta chọn phương án A.

Bài 3.28 trang 41 sách bài tập Toán lớp 10 Tập 1: Cho tam giác ABC có a = 20, b = 16 và m_a = 10. Diện tích của tam giác bằng

A. 92;

B. 100;

C. 96;

D. 88.

Lời giải:

Đáp án đúng là: C

Áp dụng công thức tính độ dài đường trung tuyến cho tam giác ABC ta có:

$m_{a}^{2} = \frac{b^{2} + c^{2}}{2} - \frac{a^{2}}{4}$

$\Rightarrow 10^{2} = \frac{16^{2} + c^{2}}{2} - \frac{20^{2}}{4}$

$\Rightarrow \frac{16^{2} + c^{2}}{2} = 10^{2} + \frac{20^{2}}{4} = 200$

$\Rightarrow$ 16² + c² = 400

$\Rightarrow$ c² = 144

$\Rightarrow$ c = 12.

Tam giác ABC có a = 20, b = 16, c = 12 nên:

• $p = \frac{a + b + c}{2} = \frac{20 + 16 + 12}{2} = 24;$

• p – a = 4;

• p – b = 8;

• p – c = 12.

Áp dụng công thức Heron ta có:

$S = \sqrt{p . (p - a) (p - b) (p - c)}$

$\Rightarrow S = \sqrt{24.4.8.12} = 96.$

Ta chọn phương án C.

Bài 3.29 trang 41 sách bài tập Toán lớp 10 Tập 1: Tam giác ABC có a = 14, b = 9 và m_a = 8. Độ dài đường cao h_a bằng

A. $\frac{24 \sqrt{5}}{7};$

B. $\frac{12 \sqrt{5}}{7};$

C. $12 \sqrt{5};$

D. $24 \sqrt{5} .$

Lời giải:

Đáp án đúng là: A

Áp dụng công thức tính độ dài đường trung tuyến cho tam giác ABC ta có:

$m_{a}^{2} = \frac{b^{2} + c^{2}}{2} - \frac{a^{2}}{4}$

$\Rightarrow 8^{2} = \frac{9^{2} + c^{2}}{2} - \frac{14^{2}}{4}$

$\Rightarrow \frac{9^{2} + c^{2}}{2} = 8^{2} + \frac{14^{2}}{4} = 113$

$\Rightarrow$ 9² + c² = 226

$\Rightarrow$ c² = 145

$\Rightarrow$ c = $\sqrt{145}$ .

Tam giác ABC có a = 14, b = 9, c = $\sqrt{145}$ nên:

• $p = \frac{a + b + c}{2} = \frac{14 + 9 + \sqrt{145}}{2} = \frac{23 + \sqrt{145}}{2};$

• p – a = $\frac{- 5 + \sqrt{145}}{2};$

• p – b = $\frac{5 + \sqrt{145}}{2};$

• p – c = $\frac{23 - \sqrt{145}}{2};$

Áp dụng công thức Heron ta có:

$S = \sqrt{p . (p - a) (p - b) (p - c)}$

$\Rightarrow S = \sqrt{\frac{23 + \sqrt{145}}{2} . \frac{- 5 + \sqrt{145}}{2} . \frac{5 + \sqrt{145}}{2} . \frac{23 - \sqrt{145}}{2}} = 24 \sqrt{5} .$