Toptailieu.vn xin giới thiệu 21 câu trắc nghiệm Bài tập cuối chương 3 Kết nối tri thức (có đáp án 2023) CHỌN LỌC, hay nhất giúp học sinh lớp 10 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.
Mời các bạn đón xem:
21 câu trắc nghiệm Bài tập cuối chương 3 Kết nối tri thức (có đáp án 2023) CHỌN LỌC
Lý thuyết
1. Giá trị lượng giác của một góc
Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O, bán kính R = 1 nằm phía trên trục hoành được gọi là nửa đường tròn đơn vị.
Cho trước một góc α, 0° ≤ α ≤ 180°. Khi đó, có duy nhất điểm M(x0; y0) trên nửa đường tròn đơn vị để ![]() = α.
= α.
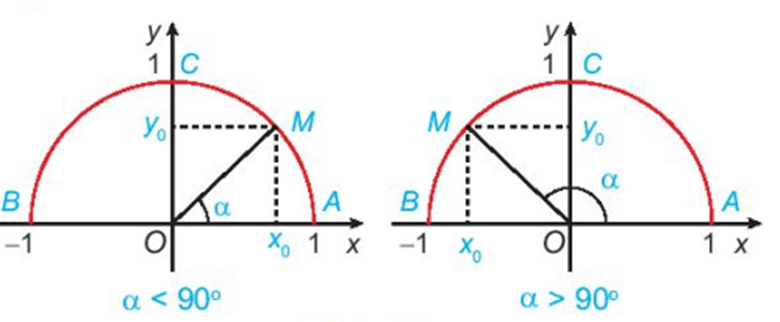
- Định nghĩa tỉ số lượng giác của một góc từ 00 đến 1800
Với mỗi góc α (0° ≤ α ≤ 180°), gọi M(x0; y0) là điểm trên nửa đường tròn đơn vị sao cho ![]() = α. Khi đó:
= α. Khi đó:
+ sin của góc α là tung độ y0 của điểm M, được kí hiệu là sin α;
+ cosin của góc α là hoành độ x0 của điểm M, được kí hiệu là cos α;
+ Khi α ≠ 90° (hay x0 ≠ 0), tang của α là ![]() , được kí hiệu là tan α;
, được kí hiệu là tan α;
+ Khi α ≠ 0° và α ≠ 180° (hay y0 ≠ 0), cotang của α là ![]() , được kí hiệu là cot α.
, được kí hiệu là cot α.
- Từ định nghĩa trên ta có:

- Bảng giá trị lượng giác (GTLG) của một số góc đặc biệt:
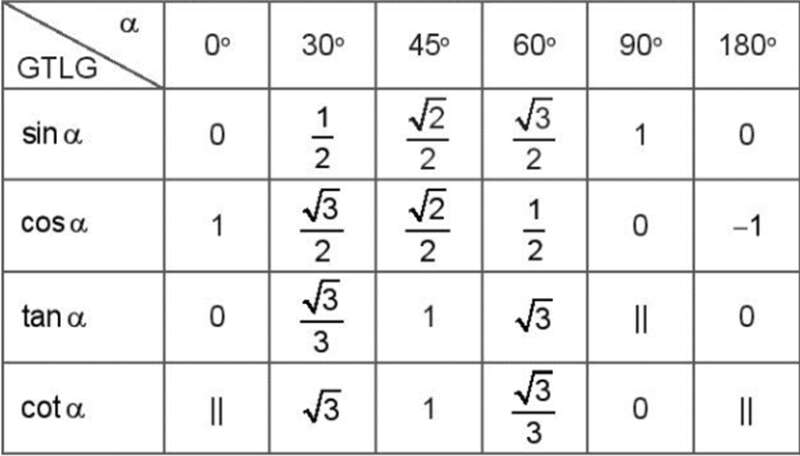
Chú ý: Kí hiệu || chỉ giá trị lượng giác tương ứng không xác định.
2. Mối quan hệ giữa các giá trị lượng giác của hai góc bù nhau.
Đối với hai góc bù nhau, α và 180° – α, ta có:
sin (180° – α) = sin α;
cos (180° – α) = –cos α;
tan (180° – α) = –tan α (α ≠ 90°);
cot (180° – α) = –cot α (0° < α < 180°).
Chú ý:
- Hai góc bù nhau có sin bằng nhau; có côsin, tang, côtang đối nhau.
- Hai góc phụ nhau có sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
3. Định lí côsin
Đối với tam giác ABC, ta thường kí hiệu A, B, C là các góc của tam giác tại đỉnh tương ứng; a, b, c tương ứng là độ dài của các cạnh đối diện với đỉnh A, B, C; p là nửa chu vi; S là diện tích; R, r tương ứng là bán kính đường tròn ngoại tiếp, nội tiếp tam giác.
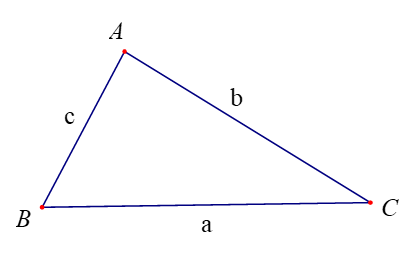
Định lí Côsin. Trong tam giác ABC:
a2 = b2 + c2 – 2bc.cosA.
b2 = c2 + a2 – 2ca.cosB.
c2 = a2 + b2 – 2ab.cosC.
4. Định lí sin
Trong tam giác ABC: ![]() .
.
5. Giải tam giác và ứng dụng thực tế
- Việc tính độ dài các cạnh và số đo các góc của một tam giác khi biết một số yếu tố của tam giác đó được gọi là giải tam giác.
Chú ý: Áp dụng định lí côsin, sin và sử dụng máy tính cầm tay, ta có thể tính (gần đúng) các cạnh và góc của một tam giác trong các trường hợp sau:
+ Biết hai cạnh và góc xen giữa.
+ Biết ba cạnh.
+ Biết một cạnh và hai góc kề.
6. Công thức tính diện tích tam giác
Đối với tam giác ABC: A, B, C là các góc của tam giác tại đỉnh tương ứng; a, b, c tương ứng là độ dài của các cạnh đối diện với đỉnh A, B, C; p là nửa chu vi; S là diện tích; R, r tương ứng là bán kính đường tròn ngoại tiếp, nội tiếp tam giác.
Ta có các công thức tính diện tích tam giác ABC sau:
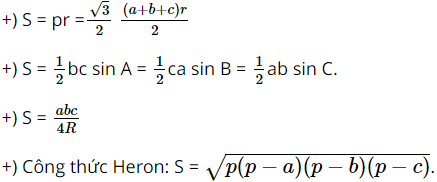
Bài tập
Câu 1: Tam giác ABC có A = 15°, B = 45° Giá trị của tanC bằng
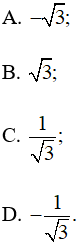
Lời giải:
Đáp án đúng là: A
Xét tam giác ABC ta có: A + B + C = 180°
⇒ C = 180° - A - B = 180° -15° - 45° = 120°
Do đó tanC = tan120° = - ![]()
Ta chọn phương án A.
Câu 2: Trên mặt phẳng toạ độ Oxy, lấy điểm M thuộc nửa đường tròn đơn vị sao cho xOM=135°. Tích hoành độ và tung độ của điểm M bằng
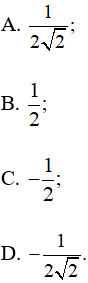
Lời giải:
Đáp án đúng là: C
Ta có xOM=135°
⇒ sinxOM = ![]() và cosxOM = -
và cosxOM = - ![]()
Mà xM = cosxOM = - 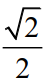 và yM = sinxOM =
và yM = sinxOM = 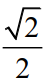
Do đó xM.yM = -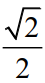 .
.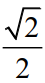 = -
= - ![]()
Ta chọn phương án C.
Câu 3: Trên mặt phẳng toạ độ Oxy, lấy điểm M thuộc nửa đường tròn đơn vị sao cho xOM=150°. N là điểm đối xứng với M qua trục tung. Giá trị của tanxON bằng
Lời giải:
Đáp án đúng là: A
Vì N đối xứng với M qua trục tung nên ta có:
• xN = –xM
⇒ cosxON = –cosxOM
⇒ cosxON = –cos150°
⇒ cosxON = - (- ![]() ) =
) = ![]()
• yN = yM
⇒ sinxON = –sinxOM
⇒ sinxON = sin150°
⇒ sinxON = ![]()
• Ta có: 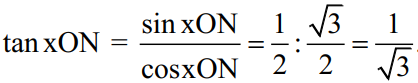
Ta chọn phương án A.
Câu 4: Cho góc nhọn α có tanα = ![]() . Giá trị của tích sinα.cosα bằng
. Giá trị của tích sinα.cosα bằng
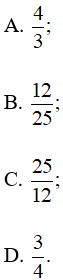
Lời giải:
Đáp án đúng là: B
Ta có: tanα = ![]() ⇒
⇒ ![]()
Do đó sinα.cosα = ![]() cosα.cosα =
cosα.cosα = ![]() cos2α.
cos2α.
Mặt khác tanα = ![]()
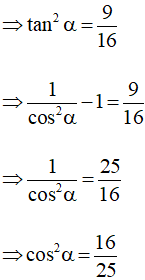
Do đó sinα.cosα = ![]()
Ta chọn phương án B.
Câu 5: Cho góc α (0° < α < 180°) thõa mãn sinα + cosα = 1. Giá trị của cotα là
A. 0;
B. 1;
C. –1;
D. Không tồn tại.
Lời giải:
Đáp án đúng là: A
Ta có: sinα + cosα = 1.
⇒ (sinα + cosα)2 = 12.
⇒ sin2α + 2.sinα.cosα + cos2α = 1.
⇒ (sin2α + cos2α) + 2.sinα.cosα = 1.
⇒ 1 + 2.sinα.cosα = 1.
⇒ 2.sinα.cosα = 0.
⇒ sinα.cosα = 0.
⇒ cosα = 0
(Vì 0° < α < 180° nên sinα > 0)
⇒ cotα = ![]() = 0
= 0
Ta chọn phương án A.
Câu 6: Cho góc α thỏa mãn sinα + cosα = ![]() . Giá trị của tanα + cotα là
. Giá trị của tanα + cotα là
A. 1;
B. –2;
C. 0;
D. 2.
Lời giải:
Đáp án đúng là: D
Ta có: sinα + cosα = ![]()
⇒ (sinα + cosα)2 = 2
⇒ sin2α + 2.sinα.cosα + cos2α = 2
⇒ (sin2α + cos2α) + 2.sinα.cosα = 2
⇒ 1 + 2.sinα.cosα = 2
⇒ 2.sinα.cosα = 1
⇒ sinα.cosα = ![]()
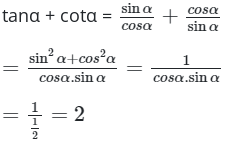
Ta chọn phương án D.
Câu 7: Trên mặt phẳng toạ độ Oxy lấy M thuộc nửa đường tròn đơn vị, sao cho ![]() (H.3.4).
(H.3.4).
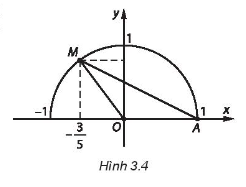
Diện tích của tam giác AOM bằng
Lời giải:
Đáp án đúng là: B
Gọi h là độ dài đường cao kẻ từ M đến OA của tam giác OAM.
Khi đó h = yM = sin![]()
Mà sin2![]() + cos2
+ cos2![]() = 1
= 1
sin2![]() = 1 – (-
= 1 – (-![]() )2
)2
sin2![]() =
= ![]()
sin2![]() =
= ![]()
Mà 90o < ![]() < 180o Þ sin
< 180o Þ sin![]() > 0
> 0
Do đó sin![]() =
= ![]()
Ta có: SΔAOM = ![]() .h.OA =
.h.OA = ![]() .
. ![]() .1 =
.1 = ![]()
Ta chọn phương án B.
Câu 8: Trên mặt phẳng tọa độ Oxy lấy điểm M thuộc nửa đường tròn đơn vị, sao cho ![]() = 150o (H.3.5).
= 150o (H.3.5).
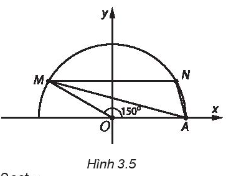
Lấy N đối xứng với M qua trục tung. Diện tích của tam giác MAN bằng
Lời giải:
Đáp án đúng là: A
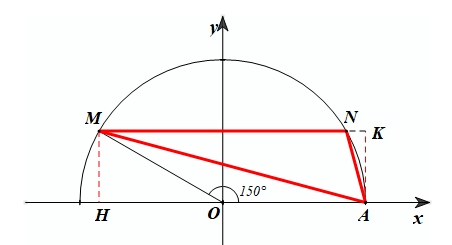
Gọi H và K lần lượt là chân đường vuông góc kẻ từ M đến Ox và kẻ từ A đến MN.
Ta có: SDAMN = ![]() .AK.MN
.AK.MN
Mà N đối xứng với M qua trục tung Oy nên ta có:
xN = –xM nên |xM| = |xN|
⇒ MN = |xM| + |xN| = 2|xM| = |2cos![]() |
|
⇒ MN = |2cos150°| = |2.(-![]() )| =
)| = ![]()
Lại có AK = MH = |yM| = |sin![]() | = |sin150°|
| = |sin150°|
⇒ AK = ![]()
Vậy SDAMN = ![]() .AK.MN =
.AK.MN = ![]() .
.![]() .
.![]() =
= ![]()
Ta chọn phương án A.
Câu 9: Cho cosα = ![]() . Giá trị của
. Giá trị của ![]() là
là
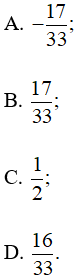
Lời giải:
Đáp án đúng là: B
Ta có cosα = ![]() Þ cos2α =
Þ cos2α = ![]()
Mà
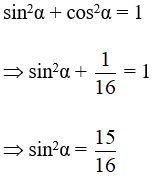
Ta có:
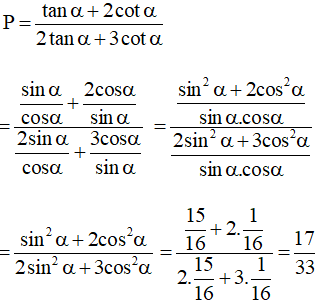
Ta chọn phương án B.
Câu 10: Tam giác ABC có a = 2, b = 3, c = 4. Bán kính đường tròn ngoại tiếp của tam giác ABC là
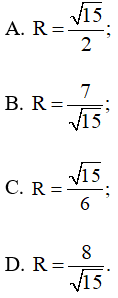
Lời giải:
Đáp án đúng là: D
Tam giác ABC có a = 2, b = 3, c = 4 nên:
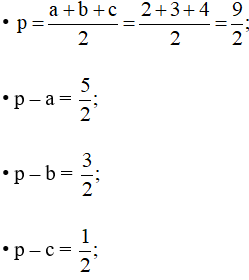
Áp dụng công thức Heron ta có:
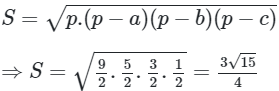
Mà
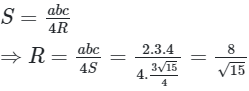
Ta chọn phương án D.
Câu 11: Tam giác ABC có a = 4, b = 5, c = 6. Độ dài đường cao hb bằng
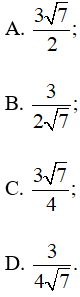
Lời giải:
Đáp án đúng là: A
Tam giác ABC có a = 4, b = 5, c = 6 nên:
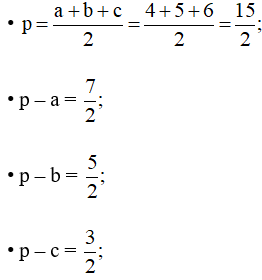
Áp dụng công thức Heron ta có:
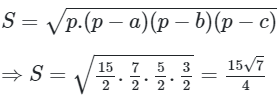
Mà
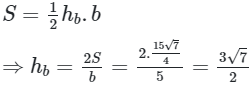
Ta chọn phương án A.
Câu 12: Cho tam giác ABC có a = 20, b = 16 và ma = 10. Diện tích của tam giác bằng
A. 92;
B. 100;
C. 96;
D. 88.
Lời giải:
Đáp án đúng là: C
Áp dụng công thức tính độ dài đường trung tuyến cho tam giác ABC ta có:
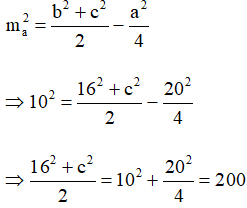
⇒ 162 + c2 = 400
⇒ c2 = 144
⇒ c = 12.
Tam giác ABC có a = 20, b = 16, c = 12 nên:
• ![]()
• p – a = 4;
• p – b = 8;
• p – c = 12.
Áp dụng công thức Heron ta có:
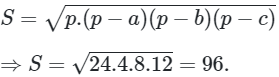
Ta chọn phương án C.
Câu 13: Tam giác ABC có a = 14, b = 9 và ma = 8. Độ dài đường cao ha bằng
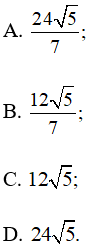
Lời giải:
Đáp án đúng là: A
Áp dụng công thức tính độ dài đường trung tuyến cho tam giác ABC ta có:
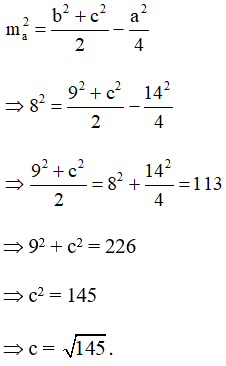
Tam giác ABC có a = 14, b = 9, c = ![]() nên:
nên:
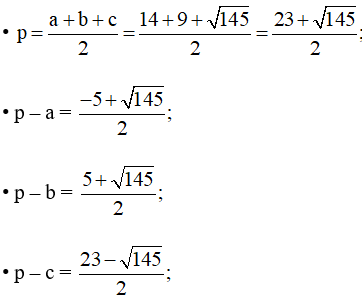
Áp dụng công thức Heron ta có:
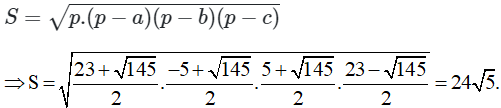
Mà:
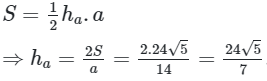
Ta chọn phương án A.
Câu 14: Tam giác ABC có ![]() = 45o, c = 6,
= 45o, c = 6, ![]() = 75o, Độ dài đường cao hb bằng
= 75o, Độ dài đường cao hb bằng
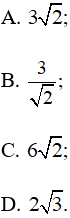
Lời giải:
Đáp án đúng là: A
Xét tam giác ABC có: ![]() +
+ ![]() +
+ ![]() = 180o
= 180o
⇒ ![]() = 180o -
= 180o - ![]() -
- ![]()
= 180o - 45o - 75o = 60o
Áp dụng định lí sin ta có:
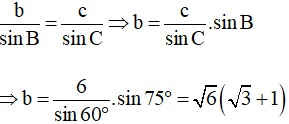
Áp dụng công thức tính diện tích tam giác ta có:
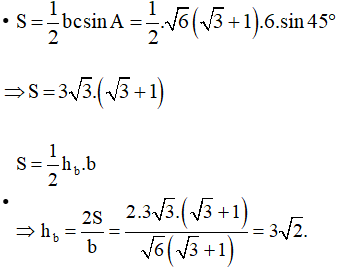
Ta chọn phương án A.
Câu 15: Tam giác ABC có c = 6, ![]() = 75o. Độ dài bán kính đường tròn ngoại tiếp của tam giác bằng
= 75o. Độ dài bán kính đường tròn ngoại tiếp của tam giác bằng
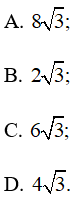
Lời giải:
Đáp án đúng là: B
Xét tam giác ABC có: ![]() +
+ ![]() +
+ ![]() = 180o
= 180o
⇒ ![]() = 180o -
= 180o - ![]() -
- ![]()
= 180o - 45o - 75o = 60o
Áp dụng định lí sin ta có:
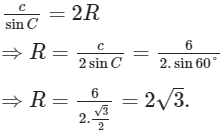
Ta chọn phương án B.
Câu 16: Tam giác ABC có diện tích S = 2R2. sin B.sinC, với R là độ dài bán kính đường tròn ngoại tiếp của tam giác. Số đo góc A bằng
A. 60°;
B. 90°;
C. 30°;
D. 75º.
Lời giải:
Đáp án đúng là: B
Áp dụng định lí sin cho tam giác ABC ta có:
![]()
⇒ a = 2R.sinA; b = 2R.sinB và c = 2R.sinC.
Theo công thức tính diện tích tam giác ta có:
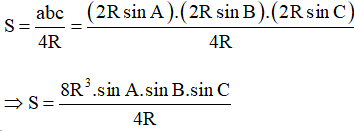
⇒ S = 2R2.sin A.sinB.sinC.
Mà theo bài S = 2R2.sinB.sinC.
Do đó sinA = 1
⇒ ![]() = 90o
= 90o
Ta chọn phương án B.
Câu 17: Tam giác ABC có AB = ![]() , AC =
, AC = ![]() và
và ![]() = 45o. Độ dài cạnh BC bằng
= 45o. Độ dài cạnh BC bằng
A. 3;
B. 2;
C. ![]()
D. ![]()
Lời giải:
Đáp án đúng là: B
Áp dụng định lí côsin cho tam giác ABC ta có:
AB2 = AC2 + BC2 – 2.AC.BC.cosC
⇒ (![]() )2 = (
)2 = (![]() )2 + BC2 – 2.
)2 + BC2 – 2.![]() .
.![]() .BC
.BC
⇒ BC2 – ![]() BC – 3 = 0
BC – 3 = 0
⇒ BC = 2 (vì BC > 0)
Ta chọn phương án B.
Câu 18: Tam giác ABC có ![]() = 60o, AC = 2 và AB =
= 60o, AC = 2 và AB = ![]() . Diện tích của tam giác ABC bằng
. Diện tích của tam giác ABC bằng
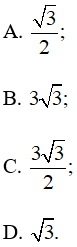
Lời giải:
Đáp án đúng là: C
Áp dụng định lí côsin cho tam giác ABC ta có:
AB2 = AC2 + BC2 – 2.AC.BC.cosC
⇒ (![]() )2 = 22 + BC2 – 2.
)2 = 22 + BC2 – 2.![]() .BC
.BC
⇒ BC2 – 2BC – 3 = 0
⇒ BC = 3 (vì BC > 0)
Áp dụng công thức tính diện tích tam giác ta có:
![]()
Ta chọn phương án C.
Câu 19: Tam giác ABC có ![]() = 60o, AB = 3 và BC =
= 60o, AB = 3 và BC = ![]() . Độ dài bán kính đường tròn nội tiếp của tam giác ABC là:
. Độ dài bán kính đường tròn nội tiếp của tam giác ABC là:
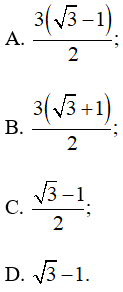
Lời giải:
Đáp án đúng là: A
Áp dụng định lí côsin cho tam giác ABC ta có:
BC2 = AB2 + AC2 – 2.AB.AC.cosA
⇒ (![]() )2 = 32 + AC2 – 2.
)2 = 32 + AC2 – 2.![]() .AC
.AC
⇒ AC2 – 3AC – 18 = 0
⇒ AC = 6 (vì AC > 0)
Áp dụng công thức tính diện tích tam giác ta có:
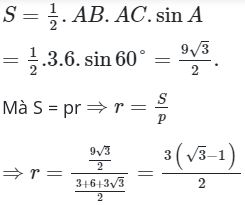
Ta chọn phương án A.
Câu 20: Một ca nô xuất phát từ cảng A, chạy theo hướng đông với vận tốc 60 km/h. Cùng lúc đó, một tàu cá, xuất phát từ A, chạy theo hướng N30°E với vận tốc 50 km/h. Sau 2 giờ, hai tàu cách nhau bao nhiêu kilômét?
A. 110 km;
B. 112 km;
C. 111,4 km;
D. 110,5 km.
Lời giải:
Đáp án đúng là: C
Giả sử chuyển vị trí của cảng A, ca nô và tàu cá sau 2 giờ chuyển động được mô tả như hình vẽ sau:
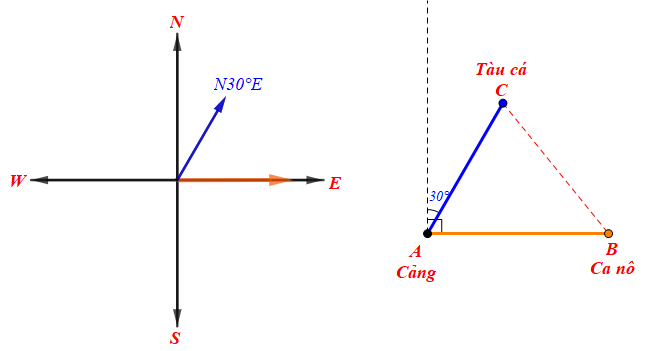
Vì ca nô chuyển động theo hướng đông và tàu cá chuyển động theo hướng N30°E nên ta có:
![]() = 90o - 30o = 60o
= 90o - 30o = 60o
Sau 2 giờ ca nô chạy được quãng đường AB bằng:
2.60 = 120 (km)
Sau 2 giờ tàu cá chạy được quãng đường AC bằng:
2.50 = 100 (km)
Áp dụng định lí côsin cho tam giác ABC ta có:
BC2 = AB2 + AC2 – 2.AB.AC.cos![]()
⇒ BC2 = 1202 + 1002 – 2.120.100.cos60°
⇒ BC2 = 12 400
⇒ BC ≈ 111,4 (km).
Ta chọn phương án C.
Câu 21: Một người đứng trên đài quan sát đặt ở cuối một đường đua thẳng. Ở độ cao 6 m so với mặt đường đua, tại một thời điểm người đó nhìn hai vận động viên A và B dưới các góc tương ứng là 60° và 30°, so với phương nằm ngang (H.3.6).
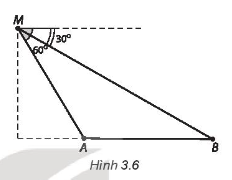
Khoảng cách giữa hai vận động viên A và B (làm tròn đến hàng đơn vị, theo đơn vị mét) tại thời điểm đó là
A. 8 m.
B. 7 m.
C. 6 m.
D. 9 m.
Lời giải:
Đáp án đúng là: B
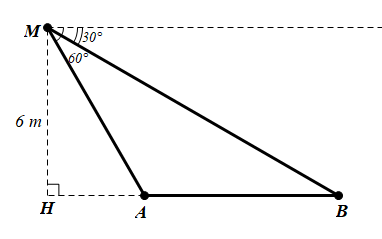
Gọi H là chân đài quan sát ở cuối đường đua.
Khi đó ta có:
• MH = 6 (m);
• ![]() = 90o - 30o = 60o;
= 90o - 30o = 60o;
• ![]() = 90o - 60o = 30o;
= 90o - 60o = 30o;
Tam giác AMH vuông tại H nên ta có:
HA = MH.tan![]() = 6.tan30° =
= 6.tan30° = ![]()
Tam giác BMH vuông tại H nên ta có:
HB = MH.tan![]() = 6.tan60° =
= 6.tan60° = ![]()
Do đó AB = HB – HA = ![]() -
- ![]() =
= ![]() ≈ 7 (m).
≈ 7 (m).
Ta chọn phương án B.
Xem thêm các bài giải Trắc nghiệm Toán lớp 10 Kết nối tri thức hay, chi tiết khác:
Bài 6: Hệ thức lượng trong tam giác
Bài 8: Tổng và hiệu của hai vecto
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.