Toptailieu.vn xin giới thiệu 69 câu trắc nghiệm Hệ thức lượng trong tam giác Kết nối tri thức (có đáp án 2023) CHỌN LỌC, hay nhất giúp học sinh lớp 10 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.
Mời các bạn đón xem:
69 câu trắc nghiệm Hệ thức lượng trong tam giác Kết nối tri thức (có đáp án 2023) CHỌN LỌC
Lý thuyết
1. Định lí côsin
Trong một tam giác bất kỳ bình phương của một cạnh sẽ bằng tổng các bình phương của hai cạnh còn lại trừ đi hai lần tích của hai cạnh đó nhân với cosin của góc xen giữa chúng. Như vậy, ta có các điều sau:
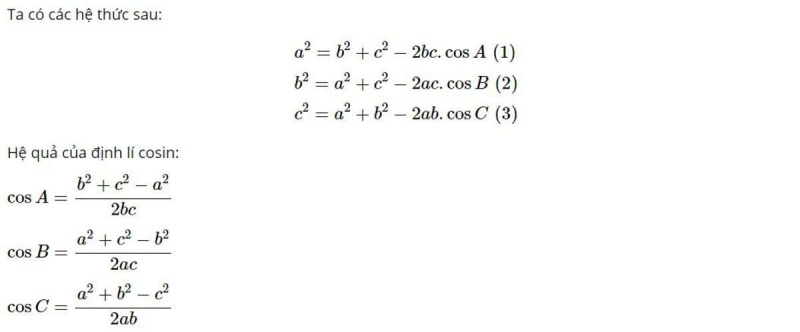
Áp dụng hệ thức lượng trong tam giác ta tính độ dài đường trung tuyến của tam giác. Trong một tam giác ABC bất kỳ ta có cạnh BC = a, cạnh CA = b, cạnh AB = c. Ta gọi ma, mb và mc là độ dài của các đường trung tuyến vẽ từ đỉnh A, B, C của tam giác:

2. Định lí sin
Trong một tam giác ABC bất kỳ, tỉ số giữa một cạnh và sin của góc đối diện với cạnh đó sẽ bằng đường kính của đường tròn ngoại tiếp tam giác. Tức là:

= = = 2R (R là bán kính của đường tròn ngoại tiếp tam giác).
3. Độ dài đường trung tuyến
Cho tam giác ABC ta có ma, mb và mc là các trung tuyến kẻ từ các điểm A, B, C. Ta có:
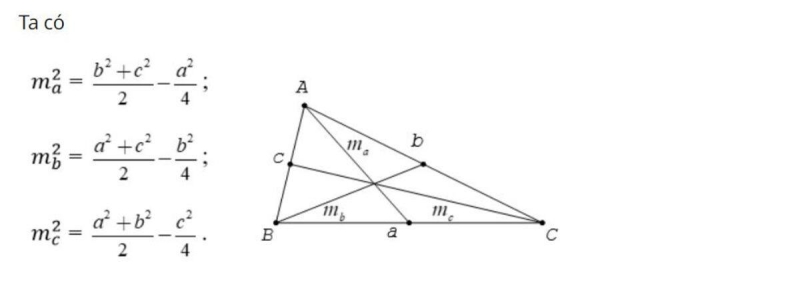
4. Công thức tính diện tích tam giác
Cho tam giác ABC có những điều sau:
ha, hb, hc là độ dài đường cao lần lượt ứng với các cạnh là BC, CA và AB.
Bán kính của đường tròn ngoại tiếp tam giác là R.
Bán kính đường tròn nội tiếp tam giác là r.
Nửa chu vi tam giác là p =
Diện tích tam giác là S.
Từ những dữ kiện kể trên ta có công thức tính diện tích tam giác là:

Bài tập
Câu 1: Cho tam giác ABC, mệnh đề nào sau đây đúng?
A. a2 = b2 + c2 + 2bc cosA. B. a2 = b2 + c2 - 2bc cosA.
C. a2 = b2 + c2 - 2bc cosC . D. a2 = b2 + c2 - 2bc cosB.
Lời giải
Chọn B
Theo định lý cosin trong tam giác ABC , ta có a2 = b2 + c2 - 2bc cosA.
Câu 2: Cho tam giác ABC , có độ dài ba cạnh là BC = a, AC = b, AB = c . Gọi ma là độ dài đường trung tuyến kẻ từ đỉnh A , R là bán kính đường tròn ngoại tiếp tam giác và là diện tích tam giác đó. Mệnh đề nào sau đây sai?
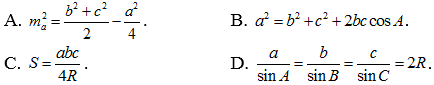
Lời giải
Chọn B
Theo định lý hàm số cosin trong tam giác ta có a2 = b2 + c2 - 2bc cosA
Câu 3: Cho tam giác ABC có a = 8, b = 10, góc C bằng 600 . Độ dài cạnh C là?
![]()
Lời giải
Chọn D
Ta có: ![]() .
.
Câu 4: Cho tam giác ABC có b = 6, c = 8, A = 600. Độ dài cạnh a là:
![]()
Lời giải
Chọn A
Ta có: ![]() .
.
Câu 5: Cho tam giác ABC có B = 600, a = 8, c = 5. Độ dài cạnh b bằng:
A. 7 B. 129 C. 49 D. ![]() .
.
Lời giải
Chọn A
Ta có: ![]() .
.
Câu 6: Cho tam giác ABC có AB = 9; BC = 8; B = 600. Tính độ dài AC.
![]()
Lời giải
Chọn A
Theo định lý cosin có:
![]()
Câu 7: Cho tam giác ABC có AB = 2, AC = 1 và A = 600. Tính độ dài cạnh BC
A. BC = ![]() B. BC = 1 C. BC =
B. BC = 1 C. BC = ![]() D. BC = 2
D. BC = 2
Lời giải
Chọn C
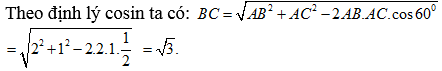
Câu 8: Tam giác ABC có a = 8, c = 3, B = 600. Độ dài cạnh b bằng bao nhiêu?
A. 49 B. ![]() C. 7 D.
C. 7 D. ![]()
Lời giải
Chọn C
Ta có: ![]() .
.
Câu 9: Tam giác ABC có C = 1500, BC = ![]() , AC = 2. Tính cạnh AB ?
, AC = 2. Tính cạnh AB ?
A.![]() . B.
. B. ![]() C. 10 . D. 1 .
C. 10 . D. 1 .
Lời giải
Chọn A
Theo định lí cosin trong tam giác ABC ta có:
![]() . Chọn A
. Chọn A
Câu 10: Cho a, b, c là độ dài 3 cạnh của tam giác ABC. Biết b = 7; c = 5; cos A = ![]() . Tính độ dài của a .
. Tính độ dài của a .
![]()
Lời giải
Chọn A
Áp dụng định lí cosin cho tam giác ABC ta có:
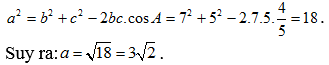
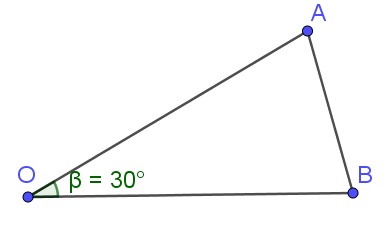
Câu 11: Cho xOy . Gọi A, B là 2 điểm di động lần lượt trên Õ, Oy sao cho AB = 2 . Độ dài lớn nhất của OB bằng bao nhiêu?
A. 4. B. 3. C. 6. D. 2.
Lời giải
Chọn A
Áp dụng định lí cosin:
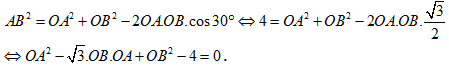 .
.
Coi phương trình là một phương trình bậc hai ẩn OA . Để tồn tại giá trị lớn nhất của OB thì ![]() .
.
Vậy max OB = 4.
Câu 12: Cho a, b, c là độ dài 3 cạnh của một tam giác. Mệnh đề nào sau đây không đúng?
A. a2 < ab + ac . B. a2 + c2 < b2 + 2ac.
C. b2 + c2 > a2 + 2bc. D. ab + bc > b2.
Lời giải
Chọn C
Do ![]() nên mệnh đề C sai.
nên mệnh đề C sai.
Áp dụng bất đẳng thức tam giác ta có ![]() ;đáp án A đúng.
;đáp án A đúng.
Tương tự ![]() ;mệnh đề D đúng.
;mệnh đề D đúng.
Ta có: ![]() ;mệnh đề B đúng.
;mệnh đề B đúng.
Câu 13: Cho tam giác ABC có AB = 4 cm, Bc = 7cm, AC = 9 cm. Tính cos A.
A. cos A = - ![]() . B. cos A =
. B. cos A = ![]() .
.
C. cos A = ![]() . D. cos A =
. D. cos A = ![]() .
.
Lời giải
Chọn D
Ta có ![]() .
.
Câu 14: Cho tam giác ABC có a2 + b2 - c2 > 0. Khi đó:
A. Góc C > 900 B. Góc C < 900
C. Góc C = 900 D. Không thể kết luận được gì về góc C
Lời giải
Chọn B
Ta có: ![]() .
.
Mà: a2 + b2 - c2 > 0 suy ra: cos C > 0 ⇒ C < 900 .
Câu 15: Cho tam giác ABC thoả mãn: b2 + c2 - a2 = ![]() bc. Khi đó:
bc. Khi đó:
A. A = 300 B. A = 450 C. A = 600 D. A = 750
Lời giải
Chọn A
Ta có: ![]()
Câu 16: Cho các điểm A(1;1), B(2;4), C(10;-2). Góc BAC bằng bao nhiêu?
A. 900. B. 600 C. 450 D. 300
Lời giải
Chọn A
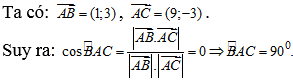
Câu 17: Cho tam giác ABC , biết a = 24, b = 13, c = 15. Tính góc A ?
A. 33034' B. 117049' C. 28037' D. 58024'
Lời giải
Chọn B
Ta có: ![]()
Câu 18: Cho tam giác ABC, biết a = 13, b = 14, c = 15 Tính góc B ?
A. 59049' B. 5307' C. 59029' D. 62022'
Lời giải
Chọn C
Ta có: ![]()
Câu 19: Cho tam giác ABC biết độ dài ba cạnh BC, CA, AB lần lượt là a, b, c và thỏa mãn hệ thức b(b2 - a2) = c(c2 - a2) với b≠c. Khi đó, góc BAC bằng
A. 450 . B. 600 . C. 900 . D. 1200.
Lời giải
Chọn D
Ta có b(b2 - a2) = c(c2 - a2) ⇔ b3 - ba2 = c3 - ca2 ⇔ b3 - c3 - a2(b-c) = 0
⇔ (b -c)(b2 + bc + c2 - a2) = 0 ⇔ b2 + c2 - a2 = -bc
Mặt khác ![]() .
.
Câu 20: Tam giác ABC có AB = c, BC = a, CA = b. Các cạnh a, b, c liên hệ với nhau bởi đẳng thức b(b2 - a2) = c(a2 - c2). Khi đó góc BAC bằng bao nhiêu độ.
A. 300 . B. 600 . C. 900 . D. 450 .
Lời giải
Chọn B
Theo bài ra, ta có:
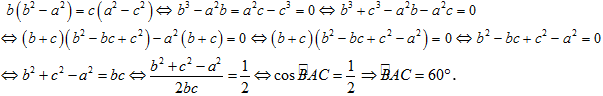
Câu 21: Cho tam giác ABC vuông cân tại A và M là điểm nằm trong tam giác ABC sao cho MA:MB:MC = 1:2:3 khi đó góc AMB bằng bao nhiêu?
A. 1350 . B. 900 . C. 1500 . D. 1200 .
Lời giải
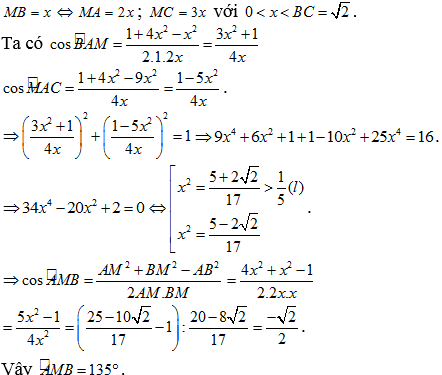
Câu 22: Cho tam giác ABC , chọn công thức đúng trong các đáp án sau:
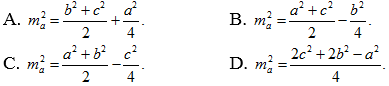
Lời giải
Chọn D
Ta có: ![]()
Câu 23: Tam giác ABC có AB = 9cm, BC = 15 cm, AC =12 cm. Khi đó đường trung tuyến AM của tam giác có độ dài là
A. 10cm . B. 9cm . C. 7,5cm . D. 8cm .
Lời giải
Chọn C
Ta có ![]()
Câu 24: Cho tam giác ABC có AB = 3cm, BC = 5cm và độ dài đường trung tuyến BM = ![]() . Tính độ dài AC.
. Tính độ dài AC.
![]()
Lời giải
Chọn B
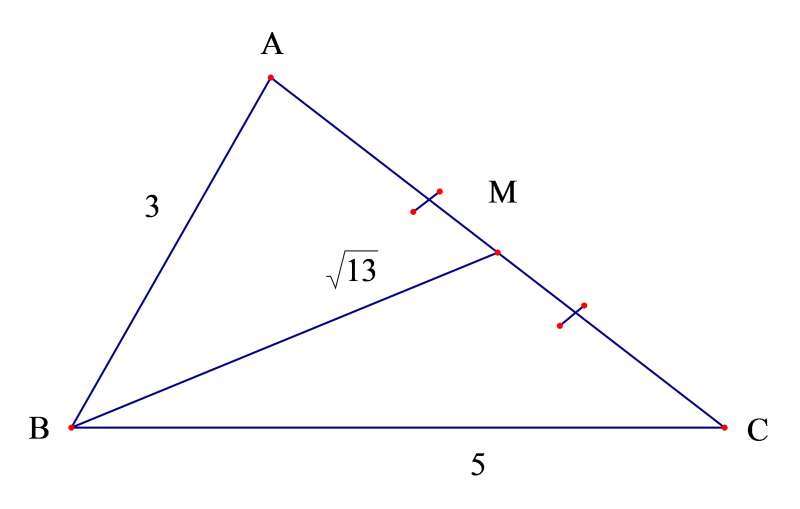
Theo công thức tính độ dài đường trung tuyến;ta có: ![]() .
.
Câu 25: Cho ΔABC vuông ở A biết C = 30o, AB = 3. Tính độ dài trung tuyến
A. 3 B. C. ![]() D.
D. ![]()
Lời giải
Chọn A
AM là trung tuyến ứng với cạnh huyền nên AM = ![]() BC = BM = MC.
BC = BM = MC.
Xét ΔBAC có B = 90o - 30o = 60o .
Xét tam giác ABM có BM = AM và B = 60o suy ra ΔABM là tam giác đều.
⇒ AM = AB = 3.
Câu 26: Tam giác ABC có a = 6, b = ![]() c = 2. M là điểm trên cạnh BC sao cho BM = 3 . Độ dài đoạn AM bằng bao nhiêu?
c = 2. M là điểm trên cạnh BC sao cho BM = 3 . Độ dài đoạn AM bằng bao nhiêu?
A. ![]() B. 9
B. 9
C. 3 D. ![]()
Lời giải
Chọn C
Ta có: Trong tam giác ABC có a = 6 ⇒ BC = 6 mà BM = 3 suy ra M là trung điểm BC
Suy ra: 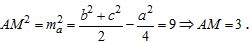
Câu 27: Gọi ![]() là tổng bình phương độ dài ba trung tuyến của tam giác ABC . Trong các mệnh đề sau mệnh đề nào đúng?
là tổng bình phương độ dài ba trung tuyến của tam giác ABC . Trong các mệnh đề sau mệnh đề nào đúng?
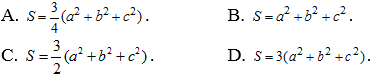
Lời giải
Chọn A
Ta có: ![]()
Câu 28: Cho ΔABC có AB = 2; AC = 3; A = 60o. Tính độ dài đường phân giác trong góc A của tam giác ABC .
![]()
Lời giải
Chọn C
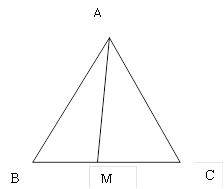
Gọi M là chân đường phân giác góc A.
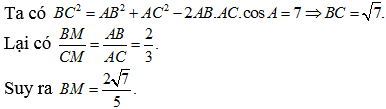
Áp dụng định lý cosin trong tam giác ABM ta được: 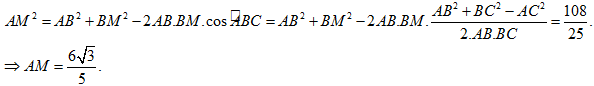
CÁCH 2
Gọi M là chân đường phân giác trong của góc A .
Vì đoạn thẳng AM chia tam giác ABC thành hai phần nên ta có:
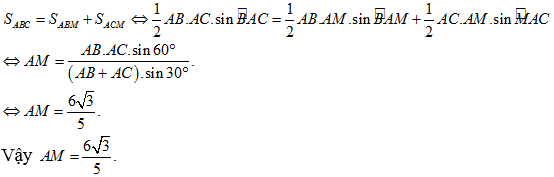
Câu 29: Cho tam giác ABC . Tìm công thức sai:

Lời giải
Chọn C
Ta có: ![]()
Câu 30: Cho ΔABC với các cạnh AB = c, AC = b, BC = a . Gọi R, r, S lần lượt là bán kính đường tròn ngoại tiếp, nội tiếp và diện tích của tam giác ABC . Trong các phát biểu sau, phát biểu nào sai?
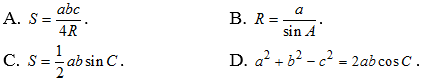
Lời giải
Chọn B
Theo định lí Sin trong tam giác, ta có ![]() .
.
Câu 31: Cho tam giác ABC có góc BAC = 60o và cạnh BC = ![]() . Tính bán kính của đường tròn ngoại tiếp tam giác ABC .
. Tính bán kính của đường tròn ngoại tiếp tam giác ABC .
A. R=4 . B. R=1 . C. R=2 . D. R=3 .
Lời giải
Chọn B
Ta có: 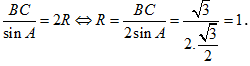 .
.
Câu 32: Trong mặt phẳng, cho tam giác ABC có AC = 4cm , góc A = 60o, B = 45o. Độ dài cạnh BC là
![]()
Lời giải
Chọn A
Ta có 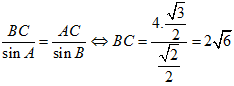 .
.
Câu 33: Cho ΔABC có AB = 5; A = 40o; B = 60o. Độ dài BC gần nhất với kết quả nào?
A. 3,7 . B. 3,3 . C. 3,5 . D. 3,1 .
Lời giải
Chọn B
C = 180o - A - B = 180o - 40o - 60o = 80o
Áp dụng định lý sin: ![]() .
.
Câu 34: Cho tam giác ABC thoả mãn hệ thức b + c = 2a . Trong các mệnh đề sau, mệnh đề nào đúng?
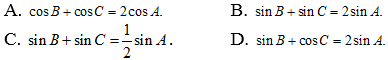
Lời giải
Chọn B
Ta có: 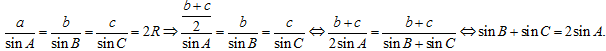
Câu 35: Tam giác ABC có a = 16,8 ; B = 56o13'; C = 71o. Cạnh c bằng bao nhiêu?
A. 29,9 B. 14,1 C. 17,5 D. 19,9
Lời giải
Chọn D
Ta có: Trong tam giác ABC : A + B + C = 180o ⇒ A = 180o - 71o - 56o13' = 52o47' .
Mặt khác ![]()
Câu 36: Tam giác ABC có A = 68o12', B = 34o44', AB = 117. Tính AC?
A. 68 B. 168 C. 118 D. 200
Lời giải
Chọn A
Ta có: Trong tam giác ABC: A + B + C = 180o ⇒ C = 180o - 68o12' - 34o44' = 77o4'.
Mặt khác ![]()
Câu 37: Chọn công thức đúng trong các đáp án sau:
A. S = ![]() bc sinA B. S =
bc sinA B. S = ![]() ac sinA
ac sinA
C. S = ![]() bc sinB D. S =
bc sinB D. S = ![]() bc sinB
bc sinB
Lời giải
Chọn A
Ta có: S = ![]() bc sinA =
bc sinA = ![]() ac sinB =
ac sinB = ![]() ab sinC.
ab sinC.
Câu 38: Cho hình thoi ABCD có cạnh bằng a. Góc BAD = 30o. Diện tích hình thoi ABCD là
![]()
Lời giải
Chọn B
Ta có SABCD = AB.AD.sinBAD = a.a.sin30o = ![]() a2.
a2.
Câu 39: Tính diện tích tam giác ABC biết AB = 3, BC = 5, CA = 6.
A. ![]() . B.
. B. ![]() . C. 6. D. 8.
. C. 6. D. 8.
Lời giải
Chọn A
Ta có: ![]() .
.
Vậy diện tích tam giác ABC là: ![]()
Câu 40: Cho ΔABC có a = 6, b = 8, c =10. Diện tích S của tam giác trên là:
A. 48 B. 24 C. 12 D. 30
Lời giải
Chọn B
Ta có: Nửa chu vi ΔABC: ![]() .
.
Áp dụng công thức Hê-rông: ![]() .
.
Câu 41: Cho ΔABC có a = 4, c = 5, B =150o. Diện tích của tam giác là:
A. ![]() B. 5 C. 10 D.
B. 5 C. 10 D. ![]()
Lời giải
Chọn B
Ta có: SΔABC = ![]() a.c.sinB =
a.c.sinB = ![]() .4.5.sin150o = 5
.4.5.sin150o = 5
Câu 42: Một tam giác có ba cạnh là 13, 14, 15. Diện tích tam giác bằng bao nhiêu?
A. 84 B. ![]() C. 42 D.
C. 42 D. ![]()
Lời giải
Chọn A
Ta có: ![]() .
.
Suy ra: ![]() .
.
Câu 43: Cho các điểm A(1;-2), B(-2;3), C(0;4). Diện tích ΔABC bằng bao nhiêu?
A. ![]() B. 13 C. 26 D.
B. 13 C. 26 D. ![]()
Lời giải
Chọn A
Ta có: ![]()
Mặt khác ![]() .
.
Suy ra: ![]()
Câu 44: Cho tam giác ABC có A(1;-1), B(3;-3), C(6;0). Diện tích ΔABC là
A. 12 B. 6 C. ![]() D. 9
D. 9
Lời giải
Chọn B
Ta có: ![]()
Mặt khác ![]() .
.
Suy ra: SΔABC = ![]() AB.BC = 6
AB.BC = 6
Câu 45: Cho tam giác ABC có a = 4, b = 6, c = 8. Khi đó diện tích của tam giác là:
![]()
Lời giải
Chọn B
Ta có: ![]()
Suy ra: ![]()
Câu 46: Cho tam giác ABC. Biết AB = 2; BC = 3 và ABC = 60o. Tính chu vi và diện tích tam giác ABC.

Lời giải
Chọn B
Ta có: AC2 = AB2 + BC2 - 2.AB.BC.cosABC = 4 + 9 - 2.2.3.cos60o = 13 - 6 = 7
Suy ra AC = ![]() .
.
Chu vi tam giác ABC là AB + AC + BC = 2 + 3 + ![]() .
.
Diện tích tam giác ABC là ![]() .
.
Câu 47: Tam giác ABC có các trung tuyến ma = 15, mb = 12, mc = 9.Diện tích S của tam giác ABC bằng
A. 72. B. 144. C. 54. D. 108.
Lời giải
Chọn A
Theo bài toán ta có
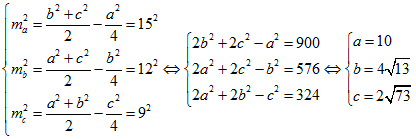
Ta có ![]() , áp dụng công thức He-rong ta có
, áp dụng công thức He-rong ta có ![]() .
.
Cách 2:
Đặt BC = a, CA = b, AB = c,
Theo định lý trung tuyến có:
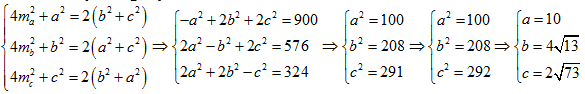
Có ![]() , Suy ra SABC = 72
, Suy ra SABC = 72
Câu 48: Cho tam giác ABC có b = 7, c = 5, cosA = ![]() . Độ dài đường cao ha của tam giác ABC là.
. Độ dài đường cao ha của tam giác ABC là.
![]()
Lời giải
Chọn A
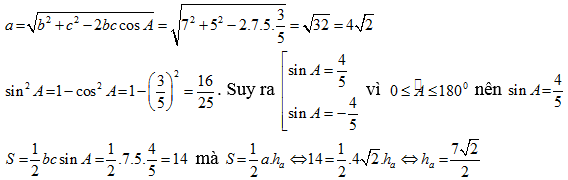
Câu 49: Cho tam giác ABC có AB = 2a, AC = 4a và BAC = 120o. Tính diện tích tam giác ABC?
A. S = 8a2. B. S = 2a2![]() . C. S = a2
. C. S = a2![]() . D. S = 4a2
. D. S = 4a2
Lời giải
Chọn B
Diện tích của tam giác ABC là SABC = ![]() AB.AC.sinBAC =
AB.AC.sinBAC = ![]() .2a.4a.sin120o = 2a2
.2a.4a.sin120o = 2a2![]() .
.
Câu 50: Cho tam giác ABC đều cạnh a. Bán kính đường tròn ngoại tiếp tam giác ABC bằng
Lời giải
Chọn B
Gọi G là trọng tâm ABC. Bán kính đường tròn ngoại tiếp ![]() .
.
Câu 51: Cho tam giác ABC có chu vi bằng 12 và bán kính đường tròn nội tiếp bằng 1. Diện tích của tam giác ABC bằng
A. 12. B. 3. C. 6. D. 24.
Lời giải
Chọn C
Theo đề bài tam giác ABC có chu vi bằng 12 nên nửa chu vi là p = ![]() ; bán kính đường tròn nội tiếp bằng 1, tức là ta có: r = 1.
; bán kính đường tròn nội tiếp bằng 1, tức là ta có: r = 1.
Diện tích tam giác ABC là: S = p.r = 6.1 = 6.
Câu 52: Cho tam giác ABC đều cạnh 2a. Tính bán kính R của đường tròn ngoại tiếp tam giác .
![]()
Lời giải
Chọn A
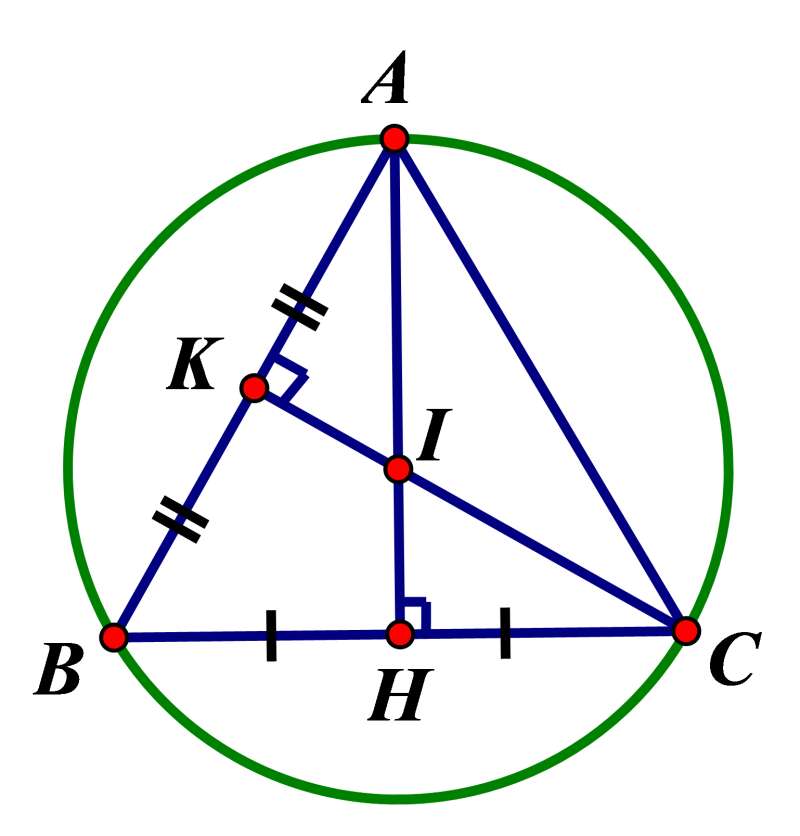
Gọi H, K lần lượt là trung điểm cạnh AB, BC
I là giao điểm của AH và CK.
Lúc đó, I là tâm đường tròn ngoại tiếp tam giác ABC
Ta có: ![]() .
.
Do đó: ![]()
Câu 53: Cho tam giác ABC có BC = ![]() , AC = 2 và AB =
, AC = 2 và AB = ![]() +1. Bán kính đường tròn ngoại tiếp tam giác ABC bằng:
+1. Bán kính đường tròn ngoại tiếp tam giác ABC bằng:
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D. 2.
. D. 2.
Lời giải
Chọn C
Áp dụng định lý cosin ta có ![]() suy ra A = 60o.
suy ra A = 60o.
Áp dụng định lý sin ta có ![]() .
.
Câu 54: Cho tam giác ABC có AB = 3, AC = 4, BC = 5. Bán kính đường tròn nội tiếp tam giác bằng
![]()
Lời giải
Chọn A
Vì AB2 + AC2 = BC2 nên tam giác ABC vuông tại A.
Do đó bán kính đường tròn nội tiếp 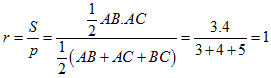 .
.
Câu 55: Cho ΔABC có S = 84, a = 13, b = 14, c = 15. Độ dài bán kính đường tròn ngoại tiếp R của tam giác trên là:
A. 8,125 B. 130 C. 8 D. 8,5
Lời giải
Chọn A
Ta có: ![]() .
.
Câu 56: Cho ΔABC có S = ![]() , nửa chu vi p = 10. Độ dài bán kính đường tròn nội tiếp r của tam giác trên là:
, nửa chu vi p = 10. Độ dài bán kính đường tròn nội tiếp r của tam giác trên là:
A. 3 B. 2 C. ![]() D.
D. ![]()
Lời giải
Chọn D
Ta có: ![]()
Câu 57: Một tam giác có ba cạnh là 26, 28, 30. Bán kính đường tròn nội tiếp là:
A. 16 B. 8 C. 4 D. ![]()
Lời giải
Chọn B
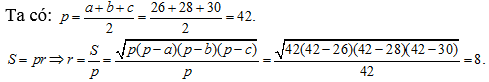
Câu 58: Một tam giác có ba cạnh là 52, 56, 60. Bán kính đường tròn ngoại tiếp là:
A. ![]() B. 40 C. 32,5 D.
B. 40 C. 32,5 D. ![]()
Lời giải
Chọn C
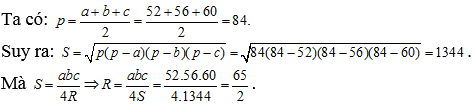
Câu 59: Tam giác với ba cạnh là 5; 12; 13 có bán kính đường tròn ngoại tiếp là?
A. 6 B. 8 C. ![]() . D.
. D. ![]() .
.
Lời giải
Chọn C
Ta có: ![]() .
.
Câu 60: Tam giác với ba cạnh là 5; 12; 13 có bán kính đường tròn nội tiếp tam giác đó bằng bao nhiêu?
A. 2 B. ![]() C.
C. ![]() D. 3
D. 3
Lời giải
Chọn A
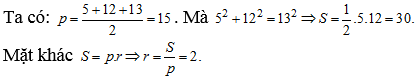
Câu 61: Tam giác với ba cạnh là 6; 8; 10 có bán kính đường tròn ngoại tiếp bằng bao nhiêu?
A. 5 B. ![]() C.
C. ![]() D. 6.
D. 6.
Lời giải
Chọn A
Ta có: ![]() .
.
Câu 62: Cho hình chữ nhật ABCD có cạnh AB = 4, BC = 6, M là trung điểm của BC, N là điểm trên cạnh CD sao cho ND = 3NC. Khi đó bán kính của đường tròn ngoại tiếp tam giác AMN bằng
![]()
Lời giải
Chọn D
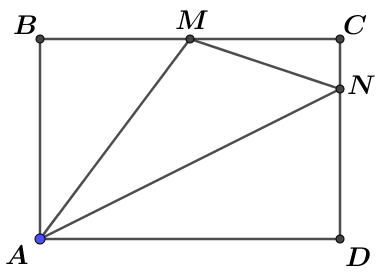
Ta có
Bán kính của đường tròn ngoại tiếp của tam giác AMN là: ![]()
Câu 63: Cho tam giác đều ABC;gọi D là điểm thỏa mãn ![]() . Gọi R và r lần lượt là bán kính đường tròn ngoại tiếp và nội tiếp của tam giác ADC. Tính tỉ số
. Gọi R và r lần lượt là bán kính đường tròn ngoại tiếp và nội tiếp của tam giác ADC. Tính tỉ số ![]() .
.

Lời giải
Chọn D
Ta có ![]() . Do đó DC = 2DB.
. Do đó DC = 2DB.
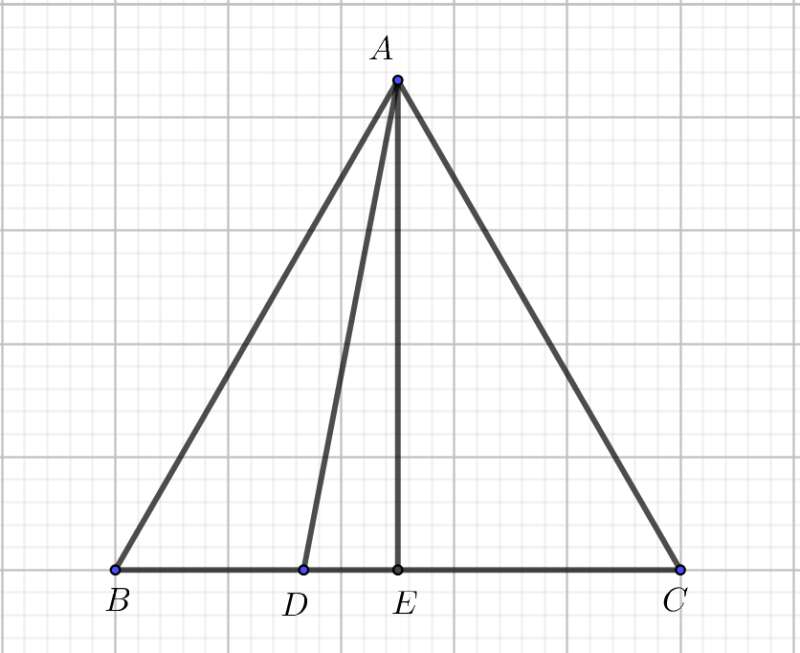
Gọi S là diện tích của tam giác ACD và E là trung điểm của BC.
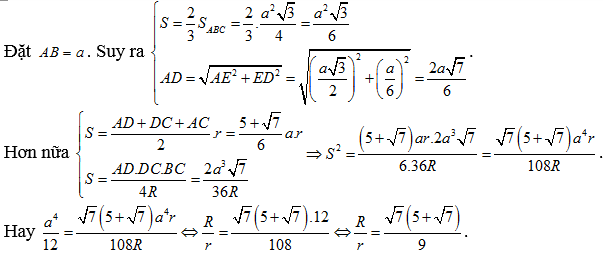
Câu 64: Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc 78o24'. Biết CA = 250m, CB = 120m. Khoảng cách AB bằng bao nhiêu?
A. 266m B. 255m C. 166m D. 298m
Lời giải
Chọn B
Ta có: AB2 = CA2 + CB2 - 2CB.CS.cosC = 2502 + 1202 - 2.250.120.cos78o24' = 64835 ⇒ AB = 255
Câu 65: Hai chiếc tàu thuỷ cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 60o. Tàu thứ nhất chạy với tốc độ 30km/h, tàu thứ hai chạy với tốc độ 40km/h. Hỏi sau 2 giờ hai tàu cách nhau bao nhiêu km?
A. 13 B. ![]() C.
C. ![]() D. 15
D. 15
Lời giải
Chọn B
Ta có: Sau 2h quãng đường tàu thứ nhất chạy được là: S1 = 30.2 = 60km
Sau 2h quãng đường tàu thứ hai chạy được là: S2 = 40.2 = 80km
Vậy: sau 2h hai tàu cách nhau là: ![]()
Câu 66: Từ một đỉnh tháp chiều cao CD = 80m, người ta nhìn hai điểm A và B trên mặt đất dưới các góc nhìn là 72o12' và 34o26'. Ba điểm A, B, D thẳng hàng. Tính khoảng cách AB?
A. 71m B. 91m C. 79m D. 40m
Lời giải
Chọn B
Ta có: Trong tam giác vuông CDA: ![]()
Trong tam giác vuông CDB: ![]()
Suy ra: khoảng cách AB = 116,7 - 25,7 = 91m
Câu 67: Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc 56o16'. Biết CA = 200m, CB = 180m. Khoảng cách AB bằng bao nhiêu?
A. 180m B. 224m C. 112m D. 168m
Lời giải
Chọn A
Ta có: AB2 = CA2 + CB2 - 2CB.CA.cosC = 2002 + 1802 - 2.200.180.cos56o16' = 32416 ⇒ AB = 180
Câu 68: Trong khi khai quật một ngôi mộ cổ, các nhà khảo cổ học đã tìm được một chiếc đĩa cổ hình tròn bị vỡ, các nhà khảo cổ muốn khôi phục lại hình dạng chiếc đĩa này. Để xác định bán kính của chiếc đĩa, các nhà khảo cổ lấy 3 điểm trên chiếc đĩa và tiến hành đo đạc thu được kết quả như hình vẽ (AB = 4,3cm; BC = 3,7cm; CA = 7,5cm). Bán kính của chiếc đĩa này bằng.
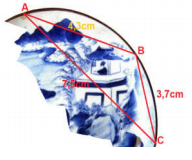
A. 5,73 cm. B. 6,01cm.
C. 5,85cm. D. 4,57cm.
Lời giải
Chọn A
Bán kính R của chiếc đĩa bằng bán kính đường tròn ngoại tiếp tam giác ABC.
Nửa chu vi của tam giác ABC là: ![]() cm.
cm.
Diện tích tam giác ABC là: ![]() cm2.
cm2.
Mà ![]() cm.
cm.
Câu 69: Giả sử CD = h là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm A, B trên mặt đất sao cho ba điểm A, B, C thẳng hàng. Ta đo được AB = 24m, CAD = 63o; CBD = 48o. Chiều cao h của khối tháp gần với giá trị nào sau đây?
A. 61,4 m. B. 18,5 m. C. 60 m. D. 18 m.
Lời giải
Chọn A
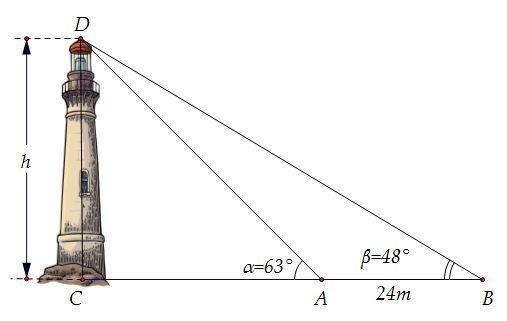
Ta có CAD = 63o ⇒ BAD = 117o ⇒ ADB = 180o - (117o + 48o) = 15o
Áp dụng định lý sin trong tam giác ABD ta có: ![]()
Tam giác BCD vuông tại C nên có: ![]()
Vậy ![]()
Xem thêm các bài giải Trắc nghiệm Toán lớp 10 Kết nối tri thức hay, chi tiết khác:
Bài 5: Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.