Giải Toán 11 trang 23 Tập 1 (Chân trời sáng tạo)

Giải Toán 11 trang 23 Tập 1 (Chân trời sáng tạo)

Ngọc Nguyễn Ngày: 07-04-2023 Lớp 11

452

Với giải SGK Toán 11 Chân trời sáng tạo trang 23 chi tiết trong Bài 3: Các công thức lượng giác giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:

Giải Toán 11 trang 23 Tập 1 (Chân trời sáng tạo)

Thực hành 4 trang 23 Toán 11 Tập 1: Tính cos $\frac{7 π}{12}$ + cos $\frac{π}{12}$ .

Lời giải:

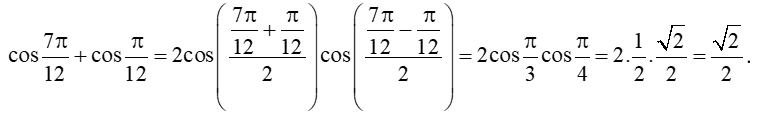
Toán 11 Bài 3 (Chân trời sáng tạo): Các công thức lượng giác (ảnh 12)

Vận dụng trang 23 Toán 11 Tập 1: Trong bài toán khởi động, cho biết vòm cổng rộng 120 cm và khoảng cách từ B đến đường kính AH là 27 cm. Tính sin α và cos α, từ đó tính khoảng cách từ điểm C đến đường kính AH. Làm tròn kết quả đến hàng phần mười.

Toán 11 Bài 3 (Chân trời sáng tạo): Các công thức lượng giác (ảnh 13)

Lời giải:

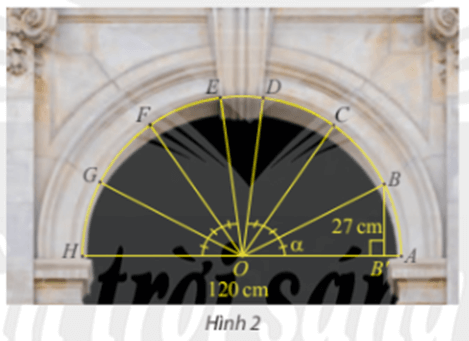
Ta có: OA = OB = $\frac{120}{2}$ = 60 cm.

Xét tam giác OBB’ vuông tại B’, có:

$\sin \hat{B O B'} = \frac{B B'}{O B} = \frac{27}{60} = \frac{9}{20}$ .

$\Rightarrow cos \hat{B O B'} = \sqrt{1 - {(\frac{9}{20})}^{2}} = \frac{\sqrt{319}}{20}$

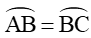Vì Toán 11 Bài 3 (Chân trời sáng tạo): Các công thức lượng giác (ảnh 14) nên sđ 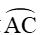= 2.sđ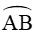 $\Rightarrow \hat{A O C} = 2 \hat{B O B'}$

Xét tam giác OCC’ vuông tại C’, có:

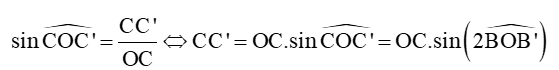
Toán 11 Bài 3 (Chân trời sáng tạo): Các công thức lượng giác (ảnh 17)

Sau bài học này ta sẽ giải quyết tiếp được bài toán như sau:

Toán 11 Bài 3 (Chân trời sáng tạo): Các công thức lượng giác (ảnh 18)

Vậy khoảng cách này từ điểm C đến AH là $60. \frac{9 \sqrt{319}}{200} \approx$ 48,2 (cm).

Bài tập

Bài 1 trang 23 Toán 11 Tập 1: Không dùng máy tính cầm tay, tính các giá trị lượng giác của các góc:

a) 5π12;

b) – 555°.

Lời giải:

a) Ta có:

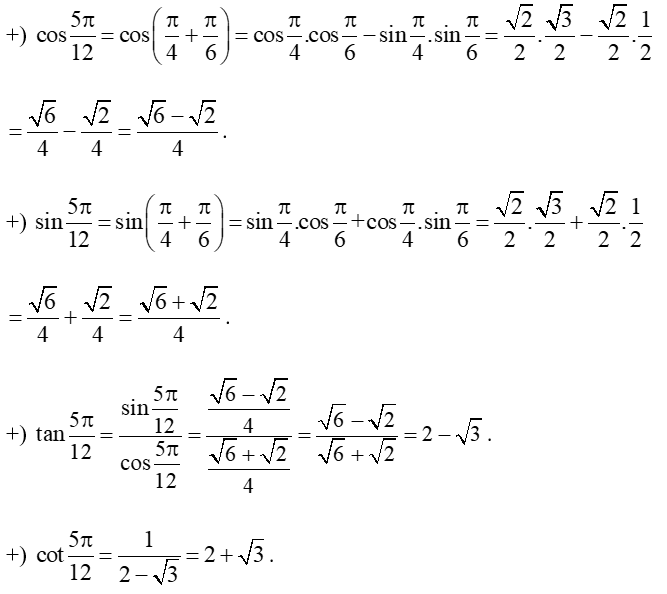
Toán 11 Bài 3 (Chân trời sáng tạo): Các công thức lượng giác (ảnh 19)

b) Ta có:

– 555° = $\frac{π . (- 555 °)}{180 °} = - \frac{37 π}{12} = - (3 π + \frac{π}{12})$ rad.

Khi đó:

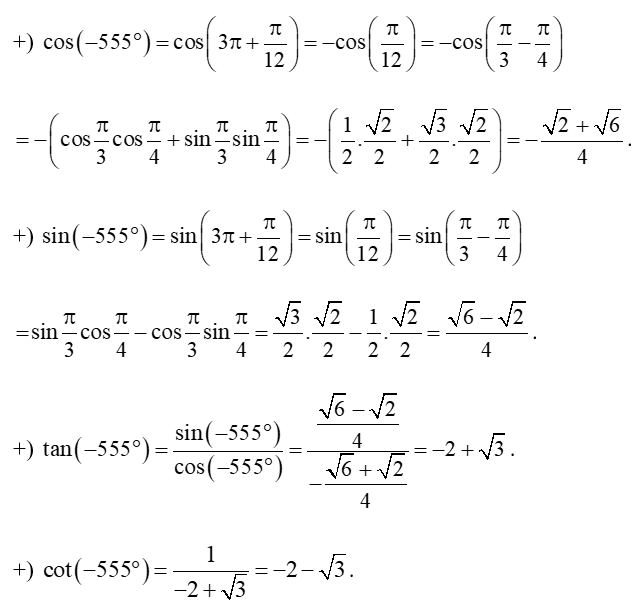
Toán 11 Bài 3 (Chân trời sáng tạo): Các công thức lượng giác (ảnh 20)

Bài 2 trang 23 Toán 11 Tập 1: Tính $\sin (α + \frac{π}{6}), cos (\frac{π}{4} - α)$ biết sin $α = - \frac{5}{13}$ và $π < α < \frac{3 π}{2}$ .

Lời giải:

Ta có: cos $α = - \sqrt{1 - {(- \frac{5}{13})}^{2}} = - \frac{12}{13}$ (vì $π < α < \frac{3 π}{2}$ ).

Ta lại có:

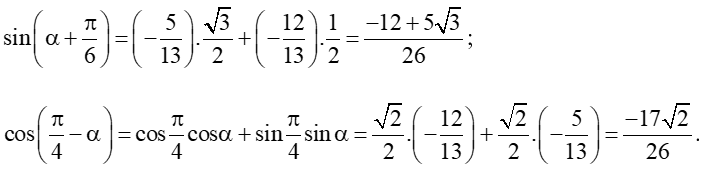
Toán 11 Bài 3 (Chân trời sáng tạo): Các công thức lượng giác (ảnh 21)

Xem thêm các bài giải Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Hoạt động khởi động trang 20 Toán 11 Tập 1: Trong kiến trúc, các vòm cổng bằng đá thường có hình nửa đường tròn để có thể chịu lực tốt. Trong hình bên, vòm cổng được ghép bởi sáu phiến đá hai bên tạo thành các cung AB, BC, CD, EF, FG, GH bằng nhau và một phiến đá chốt ở đỉnh. Nếu biết chiều rộng cổng và khoảng cách từ điểm B đến đường kính AH, làm thế nào để tính được khoảng cách từ điểm C đến AH?

Hoạt động khám phá 1 trang 21 Toán 11 Tập 1: Quan sát Hình 1. Từ hai cách tính tích vô hướng của vectơ và sau đây:

Thực hành 1 trang 21 Toán 11 Tập 1: Tính sin $\frac{π}{12}$ và tan $\frac{π}{12}$ .

Hoạt động khám phá 2 trang 21 Toán 11 Tập 1: Hãy áp dụng công thức cộng cho trường hợp β = α và tính các giá trị lượng giác của góc 2α.

Thực hành 2 trang 22 Toán 11 Tập 1: Tính cosπ8 và tanπ8.

Hoạt động khám phá 3 trang 22 Toán 11 Tập 1: Từ công thức cộng, hãy tính tổng và hiệu của: a) cos(α – β) và cos(α + β) ;

Thực hành 3 trang 22 Toán 11 Tập 1: Tính giá trị của các biểu thức sinπ24cos5π24 và sin7π8sin5π8.

Hoạt động khám phá 4 trang 22 Toán 11 Tập 1: Áp dụng công thức biến đổi tích thành tổng cho hai góc lượng

Thực hành 4 trang 23 Toán 11 Tập 1: Tính cos $\frac{7 π}{12}$ + cos $\frac{π}{12}$ .

Vận dụng trang 23 Toán 11 Tập 1: Trong bài toán khởi động, cho biết vòm cổng rộng 120 cm và khoảng cách từ B đến đường kính AH là 27 cm. Tính sin α và cos α, từ đó tính khoảng cách từ điểm C đến đường kính AH. Làm tròn kết quả đến hàng phần mười.

Bài 1 trang 23 Toán 11 Tập 1: Không dùng máy tính cầm tay, tính các giá trị lượng giác của các góc: a) 5π12;

Bài 2 trang 23 Toán 11 Tập 1: Tính $\sin (α + \frac{π}{6}), cos (\frac{π}{4} - α)$ biết sin $α = - \frac{5}{13}$ và $π < α < \frac{3 π}{2}$ .

Bài 3 trang 24 Toán 11 Tập 1: Tính các giá trị lượng giác của góc 2α, biết: a) sin $α$ = $\frac{\sqrt{3}}{3}$ và $0 < α < \frac{π}{2}$ ;

Bài 4 trang 24 Toán 11 Tập 1: Rút gọn các biểu thức sau: a) $\sqrt{2}$ sin $(α + \frac{π}{4})$ - cos $α$ ;

Bài 5 trang 24 Toán 11 Tập 1: Tính các giá trị lượng giác của góc α, biết: a) $cos 2 α = \frac{2}{5}$ và $- \frac{π}{2} < α < 0$ ;

Bài 6 trang 24 Toán 11 Tập 1: Chứng minh rằng tam giác ABC, ta có sinA = sinB.cosC + sinC.cosB.

Bài 7 trang 24 Toán 11 Tập 1: Trong Hình 3, tam giác ABC vuông tại B và có hai cạnh góc vuông là AB = 4, BC = 3. Vẽ điểm D nằm trên tia đối của tia CB thỏa mãn . Tính tan, từ đó tính độ dài cạnh CD.

Bài 8 trang 24 Toán 11 Tập 1: Trong Hình 4, pít – tông M của động cơ chuyển động tịnh tiến qua lại dọc theo xi lanh làm quay trục khuỷu IA. Ban đầu I, A, M thẳng hàng. Cho α là góc quay của trục khuỷu, O là vị trí của pít – tông khi và H là hình chiếu của A lên Ix. Trục khuỷu IA rất ngắn so với độ dài thanh truyền AM nên có thể xem như độ dài MH không đổi và gần bằng MA.

Bài 9 trang 24 Toán 11 Tập 1: Trong Hình 5, ba điểm M, N, P nằm ở đầu các cánh quạt của tua bin gió. Biết các cánh quạt dài 31m, độ cao của điểm M so với mặt đất là 30m, góc giữa các cánh quạt là và số đo góc (OA, OM) là α.

Xem thêm lời giải sách giáo khoa Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Giá trị lượng giác của một góc lượng giác

Bài 4: Hàm số lượng giác và đồ thị

Bài 5: Phương trình lượng giác

Bài tập cuối chương 1

Bài 1: Dãy số

Từ khóa :

Giải bài tập Toán 11

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

291

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

312

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

340

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

288

Tìm kiếm

Bài Viết Xem Nhiều

Bài Viết Cùng Lớp

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

2021 © All Rights Reserved.