Với giải SGK Toán 8 Chân trời sáng tạo trang 12 chi tiết trong Bài 2: Các phép toán với đa thức nhiều biến giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:
Giải Toán 8 trang 12 Tập 1 (Chân trời sáng tạo)

Lời giải:
Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:
Sau khoảng thời gian t giờ, thuyền đi xuôi dòng được quãng đường là: (v + 3).t (km).
Sau khoảng thời gian t giờ, ca nô đi ngược dòng được quãng đường là: (2v – 3).t (km).
Khoảng cách giữa hai phương tiện sau khoảng thời gian t giờ là:
(v + 3).t + (2v – 3).t
= vt + 3t + 2vt – 3t
= (vt + 3vt) + (3t – 3t)
= 4vt (km).
Vậy khoảng cách giữa chúng sau khoảng thời gian t giờ kể từ khi rời bến là 4vt (km).
1. Cộng, trừ đa thức
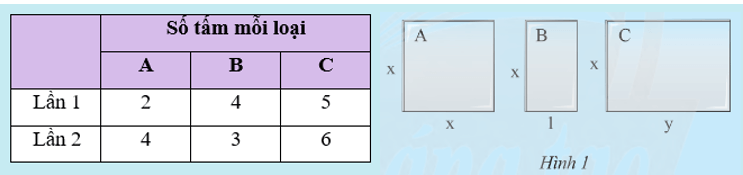
a) Tính tổng số tiền mua kính của cả hai lần.
b) Số tiền lần 2 nhiều hơn lần 1 bao nhiêu?
Lời giải:
a) Giá tiền của tấm kính chống nắng loại A là: a.SA = a.(x.x) = ax2 (đồng).
Giá tiền của tấm kính chống nắng loại B là: a.SB = a.(x.1) = ax (đồng).
Giá tiền của tấm kính chống nắng loại C là: a.SC = a.(x.y) = axy (đồng).
Số tiền mua kính của lần 1 là: 2ax2 + 4ax + 5axy (đồng).
Số tiền mua kính của lần 2 là: 4ax2 + 3ax + 6axy (đồng).
Tổng số tiền mua kính của cả hai lần là:
(2ax2 + 4ax + 5axy) + (4ax2 + 3ax + 6axy)
= 2ax2 + 4ax + 5axy + 4ax2 + 3ax + 6axy
= (2ax2 + 4ax2) + (4ax + 3ax) + (5axy + 6axy)
= 6ax2 + 7ax + 11axy (đồng).
b) Số tiền lần 2 nhiều hơn lần 1 là:
(2ax2 + 4ax + 5axy) – (4ax2 + 3ax + 6axy)
= 2ax2 + 4ax + 5axy – 4ax2 – 3ax – 6axy
= (2ax2 – 4ax2) + (4ax – 3ax) + (5axy – 6axy)
= –2ax2 + ax – axy (đồng).
Xem thêm các bài giải SGK Toán 8 Chân trời sáng tạo hay, chi tiết khác:
Thực hành 1 trang 13 Toán 8 Tập 1: Cho hai đa thức M = 1 + 3xy – 2x2y2 và N = x – xy + 2x2y2.
Thực hành 2 trang 14 Toán 8 Tập 1: Thực hiện các phép nhân đơn thức sau: (4x3).(–6x3y);
Thực hành 3 trang 15 Toán 8 Tập 1: Viết các biểu thức sau thành đa thức: (–5a4)(a2b – ab2);
Vận dụng 2 trang 15 Toán 8 Tập 1: Tính diện tích phần tô màu trong Hình 4.
Thực hành 4 trang 16 Toán 8 Tập 1: Thực hiện phép chia 8x4y5z3 cho 2x3y4z
Thực hành 5 trang 16 Toán 8 Tập 1: Thực hiện các phép chia:(5ab – 2a2) : a;
Bài 1 trang 17 Toán 8 Tập 1: Tính: x + 2y + (x – y);
Bài 3 trang 17 Toán 8 Tập 1: Thực hiện phép nhân 3x(2xy – 5x2y);
Bài 4 trang 17 Toán 8 Tập 1: Thực hiện phép nhân (x – y)(x – 5y);
Bài 5 trang 17 Toán 8 Tập 1: Thực hiện phép chia 20x3y5 : (5x2y2);
Bài 6 trang 17 Toán 8 Tập 1: Thực hiện phép chia (4x3y2 – 8x2y + 10xy) : (2xy);
Xem thêm các bài giải SGK Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Đơn thức và đa thức nhiều biến
Bài 3: Hằng đẳng thức đáng nhớ
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.